Ricci 流在任意度量时刻的Immortal 解

赵成兵

(1.安徽建筑工业学院数学系, 安徽 合肥230022;2.合肥工业大学管理学院, 安徽合肥230009)

1 引言

设M是完备非紧的复n维的Kähler 流形,它的全纯双截曲率非负且有界,Ricci 流

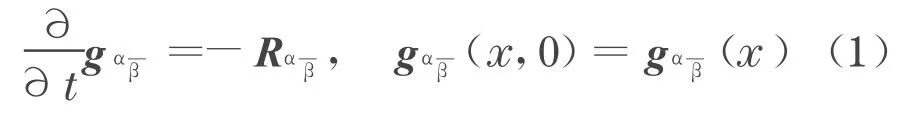
是通过Ricci 张量Rαβ—来发展M上的Kähler 度量gαβ—,它最先由Hamilton[2]介绍而来, 后来他研究Ricci 流的奇异模, 他把奇异模分为三类[2],前面的两类分别叫Eternal 解和Ancient 解, 最后的叫Immortal 解, 就是说Ricci 流有光滑解在上,且,这里R(x,t)表示在时刻t的数量曲率,C是正的常数.Chen 和Zhu[3]证明Immortal 解存在, 如果M是复n维完备非紧的Kähler 流形有有界的正的曲率算子, 它的测地球有欧式体积增长, 他们利用这个结果去研究由Yau提出的单值化问题[4-6],在n=2 时他们得到这个猜测是对的, 即对任意完备非紧的Kähler 曲面有正的有界的全纯双截曲率, 如果它的测地球有欧式体积增长, 那么它是双全纯于C2,这是到目前为止最好的结果.Shi 也证明Immortal 解的存在假设开始曲率有二次退化[4],最近Ni 和Tam[5]通过Poincaré-Lelong 方程去研究Ricci 流, 他们简化Shi 的讨论并且得到一些好的结果.

定理1 设M是n维完备非紧的Kähler 流形,有有界非负的全纯双截曲率, 如果存在常数C,使得CR(x,t)≥R(x,0), 那么Ricci 流(见式(1))有Immortal 解当且仅当

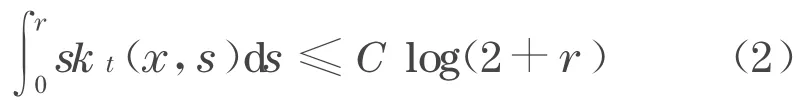
对某个常数C＞0 ,对所有的x∈M,r≥0 ,这里

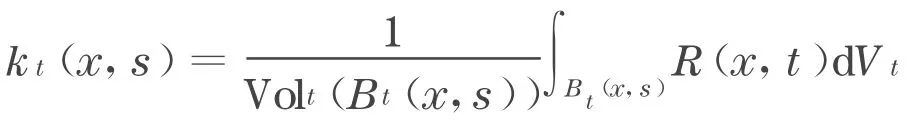
式中:Volt(B t(x,s))是测地球B t(x,s)中心在x∈M半径s的体积,R(x,t)是M的数量曲率.

2 Immortal 解存在的必要条件

引理1[2]设M是n维完备非紧的Kähler 流形,有有界非负的全纯双截曲率, 如果存在常数C,使得对∀x,y∈M,

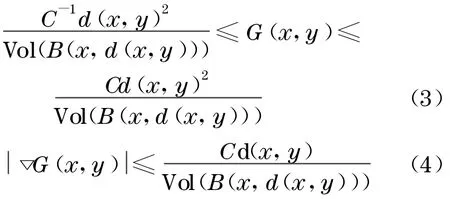
这里d(x,y)表示x和y在gαβ—(x)度量下的测地距离, ▽是表示gαβ—(x)的梯度,G(x,y)是M在开始度量gαβ—(x)下的正的Green 函数.

引理2[5]设M是n维完备非紧的Kähler 流形,有有界非负的全纯双截曲率, 假设式(1)有长时间的解, 使得对任意的T＞0 ,满足下面的情况

(i)对0 ≤t＜T,(M,gαβ—(x,t))是Kähler 度量有非负有界的双截曲率

(ii)这里存在常数C＞0,使得

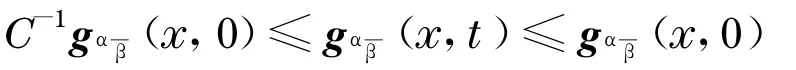
且0 ＜R(x,t)≤C,对所有的(x,t)∈M×[0 ,T),假设∫r

0sk(x,s)ds≤C1log(2 +r),对某个常数C1＞0 ,对所有的x和r,那么

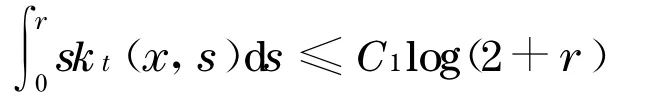
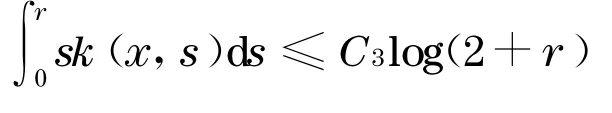
证明 从文献[2] 知

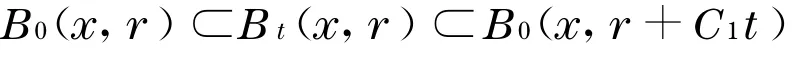
那么

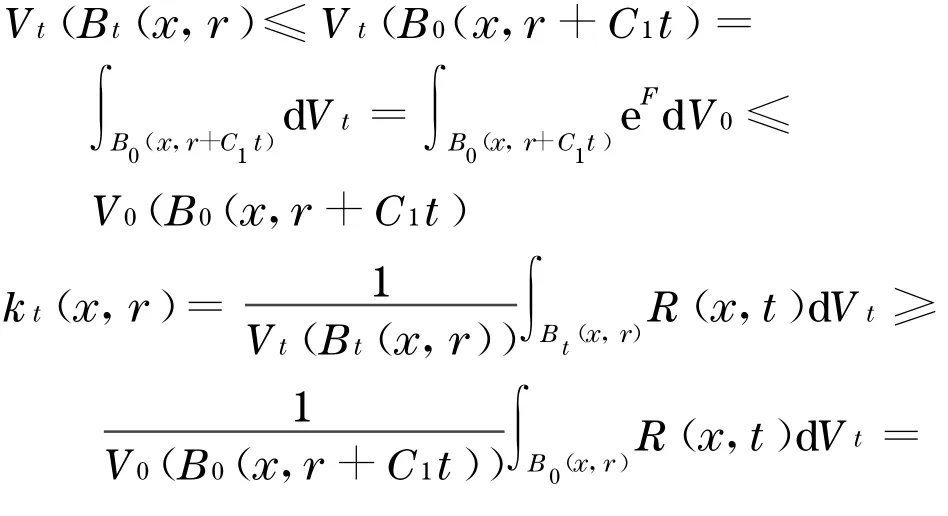
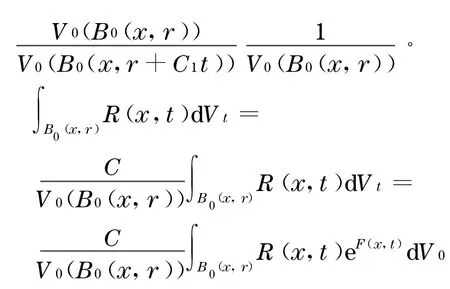
让Fmint=infx∈MF(x,t)

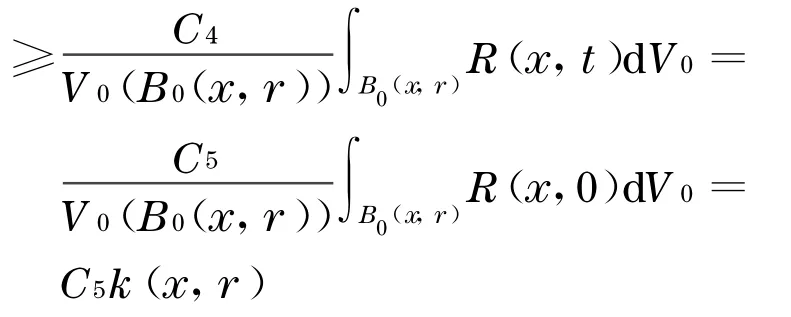
因为R(x,t)是有界的,所以存在C6,使得C6R(x,t)＞R(x,0), 所以

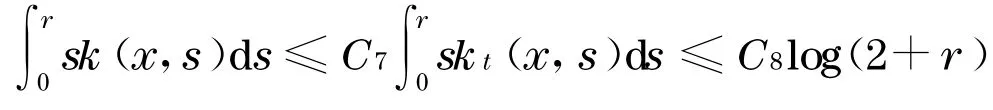
引理4[1]设M是n维完备非紧的Kähler 流形,有有界非负的全纯双截曲率, 定理1 的条件成立, 那么存在常数C＞0 使得对∀x∈M,r＞0 ,有

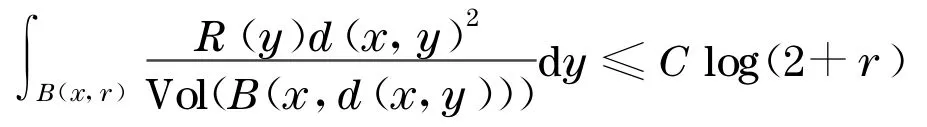
引理5[5]设M是n维完备非紧的Kähler 流形, 有有界非负的全纯双截曲率, 那么Poincaré-Lelong 方程有一个解且对常数C＞0 和所有的r＞0 ,当且仅当对常数C′＞0 .

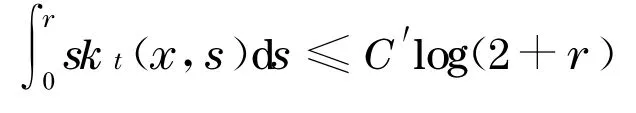
下面证明定理1 的必要条件

证明 从引理5 知道只要证明Poincaré-Lelong方程有一个解且, 那么得到定理1 的必要条件

为解Poincaré-Lelong 方程,首先构造一组近似解u r如下.

对一个固定的x0∈M和∀r＞0 ,定义u r(x)在B(x0,r)上由

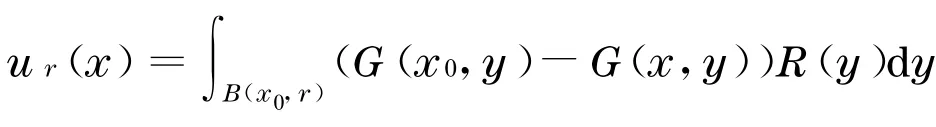
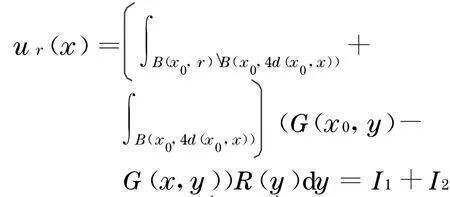
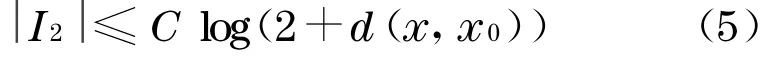
由式(4), 有对y∈B(x0,r)4d(x0,x),

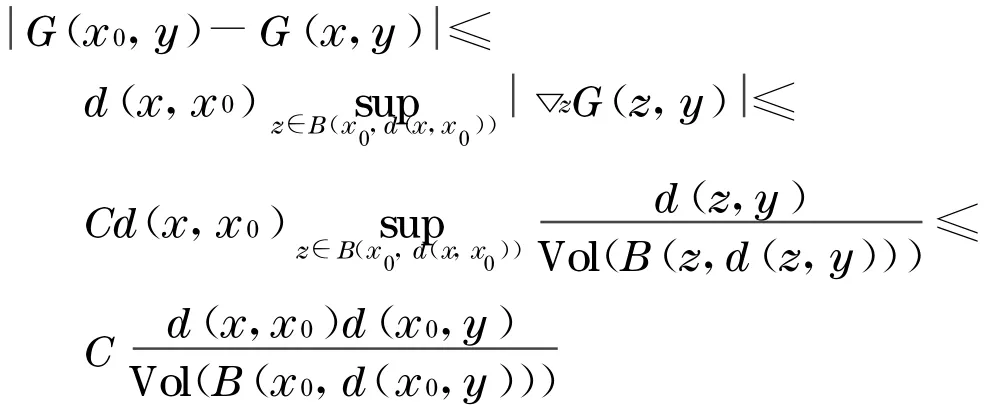
结合引理4,有

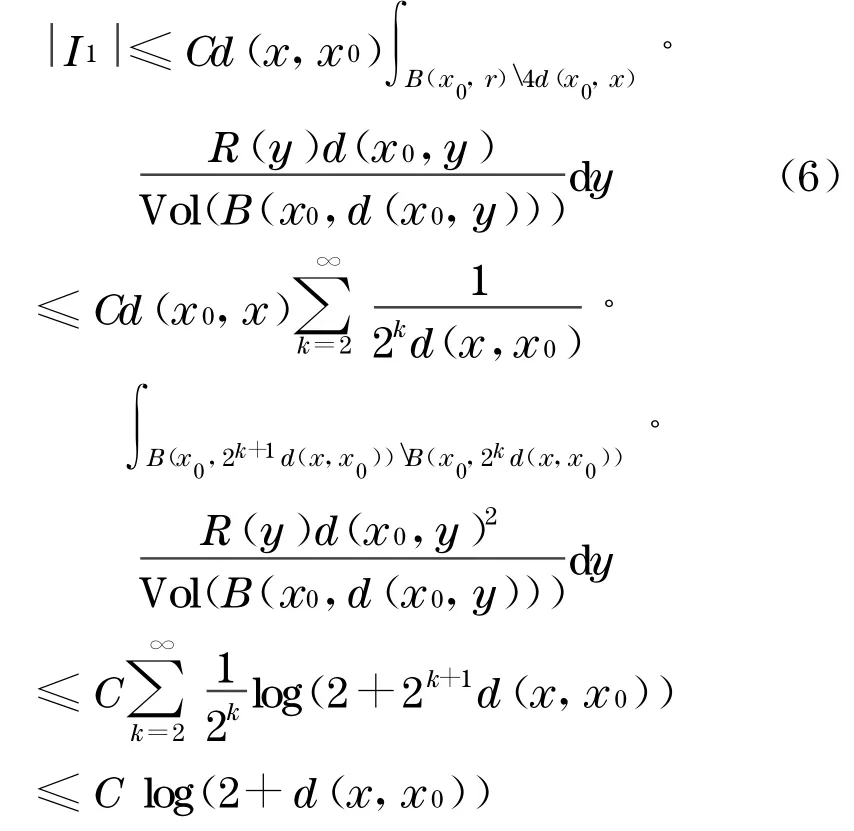
由式(5),(6)得到

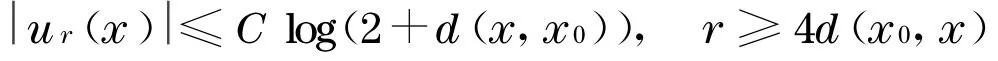
因此由Schauder 关于椭圆方程的定理 存在系列r j→+∞使得u rj(x)一致收敛到M上紧子集上的光滑函数u满足

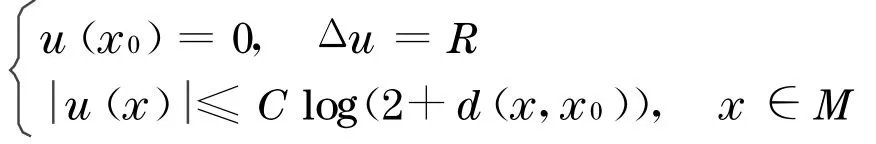
现在证明Poincaré-Lelong 方程有解.

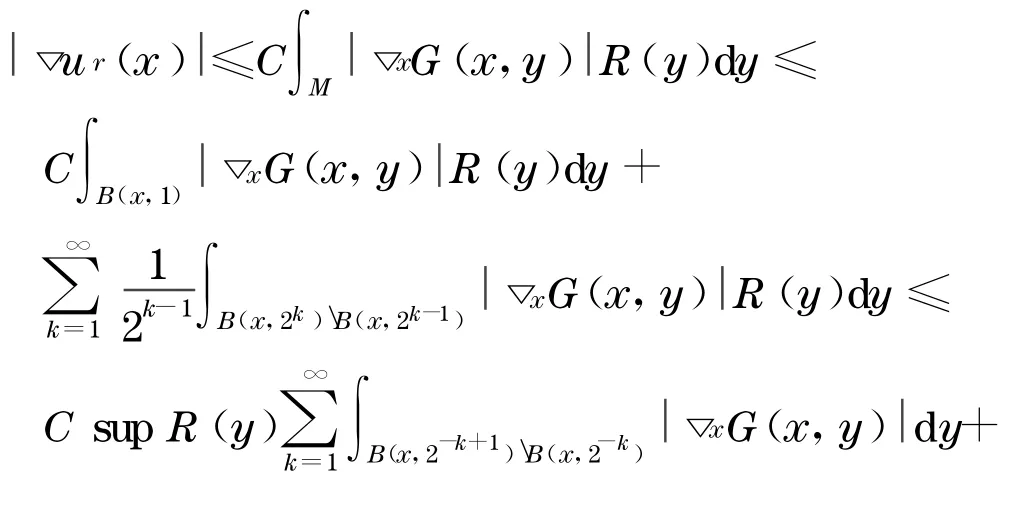
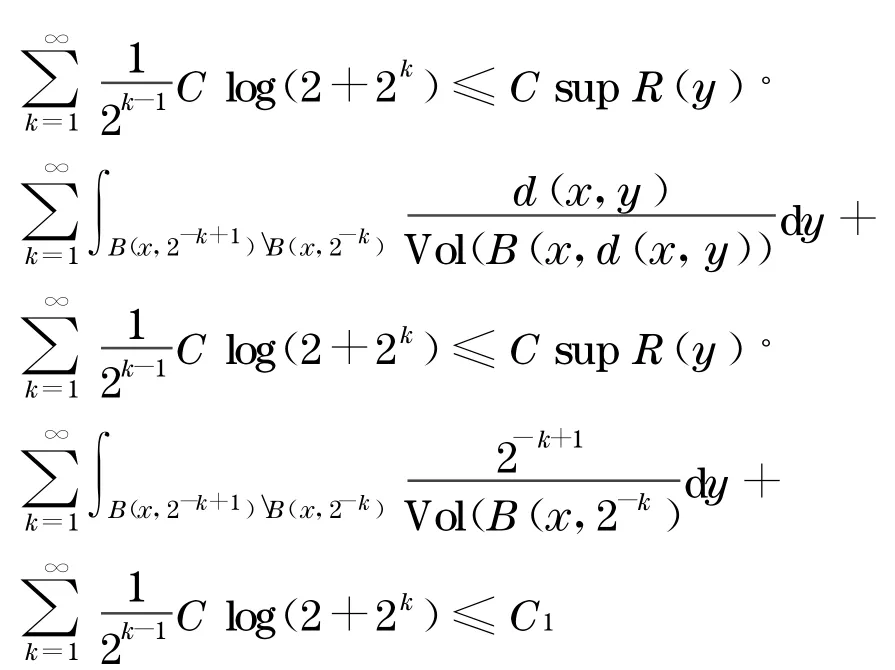
由Bochner 恒等式和Δu=R

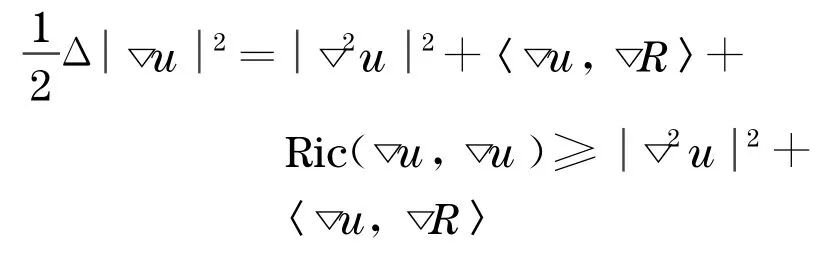
乘以截断函数并分布积分

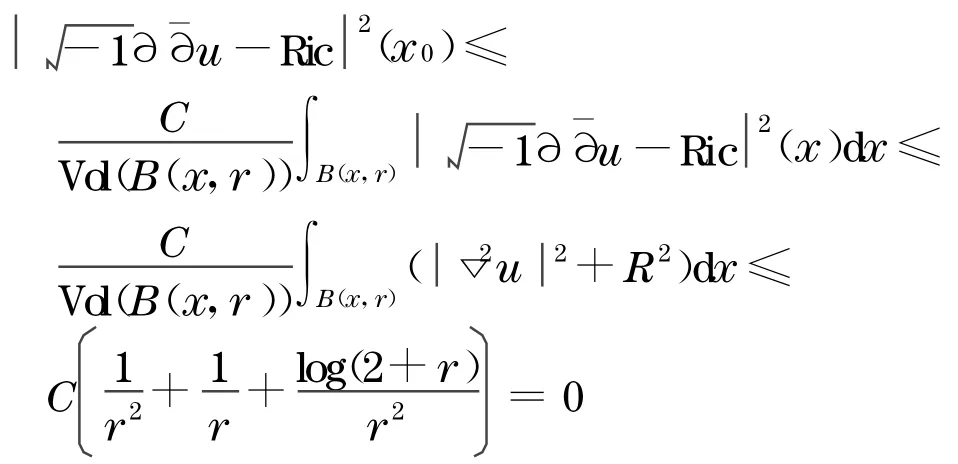
当r→∞, 知道在M上, 此外由引理3 ,那么证明定理1 的必要条件.

对于Immortal 解的充分条件可以参考文献[1] .

致谢:衷心感谢同济大学数学系陈志华教授对本文的指导和帮助.

[1] RUAN Qihua, CHEN Zhihua.Immortal solution of the Ricci flow[J] .Science in China, Series A Math, 2005(S1):217.

[2] Hamilton R S.Formation of singularities in the Ricci flow[C] ∥Surveys in Differential Geometry.[S.l.] :International Press ,1995:7-136.

[3] CHEN Binglong, ZHU Xiping.A uniformization theorem of complete noncompact Kähler surface with positive bisection curvature[J] .Journal Diff Geom, 2004, 67(3):519.

[4] SHI Wangxiong.Ricci flow and the uniformization on complete noncompact Kähler manifolds[J] .Journal Diff Geom, 1997, 45(1):94.

[5] NI Lei, Tam Luenfai.Kä hler Ricci flow and the Poincaré-Lelong equation[J] .Comm Anal Geom, 2004, 12(1):111.

[6] ZHAO Chengbing.Uniformization theorem on complete Kä hler manifolds[J] .Journal of Tongji University:Natural Science,2007, 35(8):1108.