基于拓展Tullock 模型的开发商寻租博弈均衡策略

刘天虎 ,黄武军 ,许维胜 ,吴启迪,

(1.同济大学 电子与信息工程学院, 上海200092;2.同济大学经济与管理学院, 上海200092)

早在1980 年Tullock[1]就提出了寻租博弈的概念, Tullock 分析了寻租成本, 发现企业垄断地位的获取是有成本的, 且寻租中的企业垄断会通过竞争实现均衡, 均衡的结果使寻租成本与经济租的量值相等.Tullock 进一步揭示了政府在对经济主体实施行政干预的过程中会造成资源的紧张, 诱发寻租行为,导致社会资源的浪费.Perez-Castrillo 等[2]证明了Tullock 寻租博弈模型具有唯一的纯策略Nash均衡.Bruce[3]分析了寻租博弈者的风险中性行为模式,提出了Stackelberg 博弈模型, 实现了在不完全信息下的子博弈均衡.次年, Bruce[4]研究了重复寻租博弈中的合作行为, 利用重复博弈的特性来维持寻租的合作性, 并将Nash 谈判均衡应用于对称和不对称的寻租环境中.Skaperdas 等[5]研究了两位具有风险厌恶特性的博弈方的纯策略N ash 均衡的存在条件.Szidarovszky 等[6]证明了在生产函数严格递增且呈凸性的情况下,寻租博弈的非对称纯策略Nash均衡的唯一存在性.在此博弈中, 所有参与者都假定为风险中性的.William[7]建立了N位对称竞争对手的寻租博弈模型,每位博弈方都对寻租有不同赋值,且各自能力不同, 其中一位基于Tullock 概率能获胜,由此得到纯策略Nash 均衡.Cornes 等[8]允许风险厌恶的博弈方参与Szidarovszdy 寻租博弈模型,证明了纯策略Nash 均衡的存在.David 等[9]给出了对称寻租博弈的纯策略Nash 均衡, 在竞争成功函数同质的条件下均衡策略具有简单模式, 并给出了均衡存在的充分条件.Matros[10]对T ullock 寻租博弈模型进行了扩展,证明了随着租金费用的增加,寻租人成功的机会将减少, 更多寻租人的参与将导致租金发生变动, 得到了寻租博弈的纯策略均衡.Riechmann[11]建立了局中人相对支付最大化的Tullock 寻租博弈数学模型, 研究表明, 局中人倾向于为寻租过程过度投入, 租金的耗费与局中人数量无关.Yamazaki[12-13]假定博弈方受到寻租活动的收益及预算约束, 其均衡受到一定的限制,基于对称寻租博弈的特点, 证明了纯策略Nash 均衡的存在.Matros[14]分析了存在补偿条件下的Tullock 寻租博弈模型,研究表明获得补偿的局中人将最大化边际支付,而失去补偿的局中人将最小化边际支付, 并证明了均衡策略的唯一性.Schoonbeek[15]分析了存在潜在进入者的两阶段Tullock 寻租博弈模型, 第一阶段通过贿赂来规避竞争,第二阶段则实施寻租竞争,得到了存在潜在进入者的均衡策略.

而房地产开发商对土地资源的寻租实际上也是一种不完全信息博弈, 博弈各方的信息是不对称的[16-17] .由于寻租竞争的存在, 开发商有机会获得寻租的成功,也可能会失败, 可见开发商面对的是不确定性条件下的选择, 各位开发商的风险态度会影响他的行为.本文将对T ullock 寻租博弈模型进行扩展,研究开发商土地寻租博弈的均衡解.

1 经典Tullock 模型

Tullock[1]提出了经典的寻租博弈理论, 基于Tullock 的寻租博弈模型,若令N≡{1 ,2,…,n}为N位博弈局中人, 局中人i为获取胜利而付出的努力可用x i表示,X=(x1,x2,…,xn), 其中局中人i获取胜利的概率可表示为πi(X), 令(π1,π2,…, πn)为竞争成功函数, 对于寻租博弈的成功而言, 所有局中人都有一个普遍一致的估值VAL,在局中人都是风险中性的前提下,局中人i的期望效用为

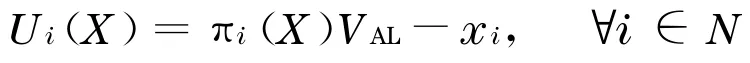
Tullock 的竞争函数可表示为[18]

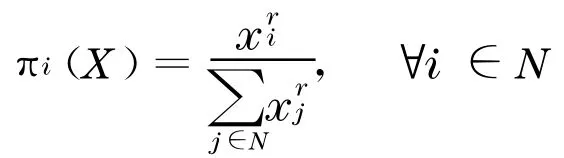
其中,r＞0 .

Skaperdas[19]通过5 条公理对Tullock 竞争函数进行了完整的描述:

公理1 (可能性)对于 ∀i∈N,∀X,有如果x i＞0 ,则有πi(X)＞0 .

公理2 (单调性)对于∀i∈N,∀j≠i,πi(X)在xi域是递增的,在x j域是递减的.

公理4 (独立性)对于∀S⊂N,∀i∈S,πSi(X)与集合S之外的博弈参与人是相互独立的.

公理5 (同质性)对于∀t＞0,∀X,∀i∈N,有πi(tX)=πi(X).

公理1 和公理2 表明Tullock 竞争成功函数具有概率函数的特性, 局中人增加努力会使其成功的可能性增大,从而使其他局中人的成功机会减少.公理3 表明任何两位局中人在相同努力下的成功可能性是相同的.公理4 表明如果某位局中人a1 未能获胜,则a1对于其他局中人的获胜可能性不带来影响.公理5 表明任意两位局中人的努力具有同质性.

2 寻租博弈分析

2 .1 寻租博弈模型的改进

同样,可将寻租的期望效用推广到N位开发商竞争的模式,则eTi可由n×n的矩阵表示,用来表示开发商的效用支付:

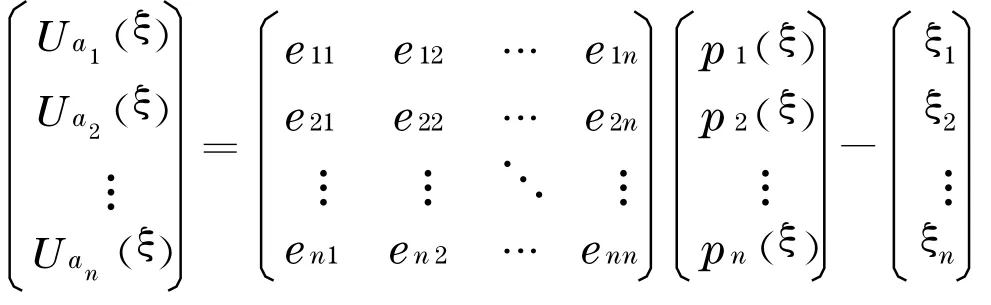
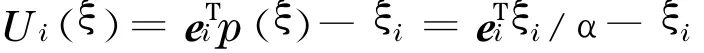
为了得到开发商a1的最优支付条件, 需对U a1(ξ)求偏导:

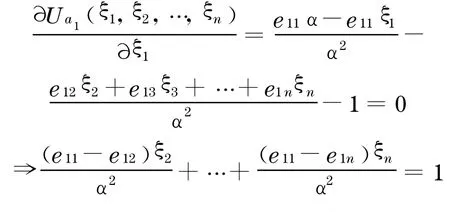
用同样的方法, 可以得到每一位开发商的最优支付条件如下:

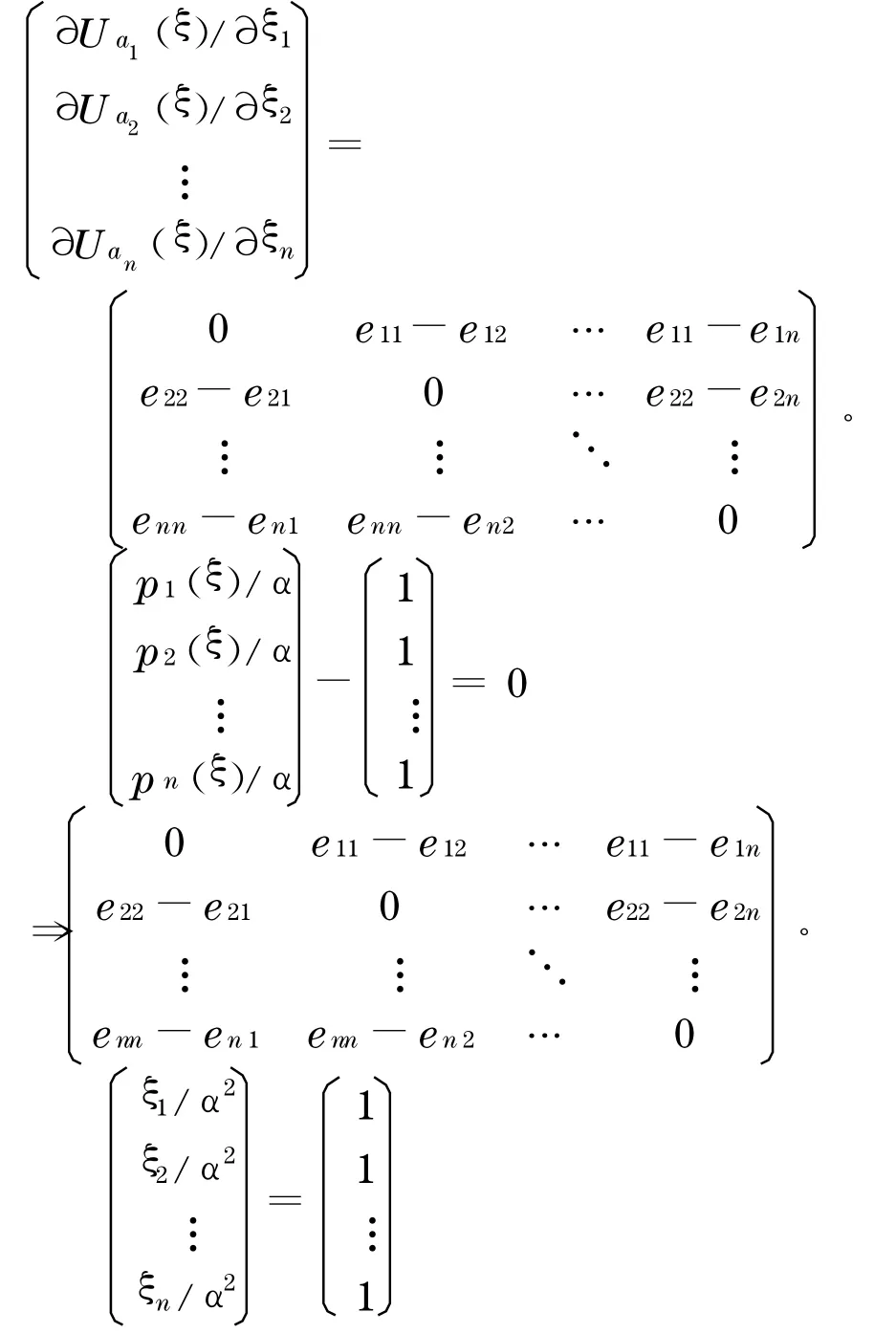
通过计算等式两边的值, 可以得到Nash 均衡解,虽然计算比较复杂, 但通过Matlab 编程可简化计算过程.为了简化分析过程, 接下来以三位房地产开发商a1,a2,a3的寻租博弈为例进行研究.

2.2 均一估值分析

对于房地产开发商而言, 土地寻租的效益决定了开发商付出的程度, 如果对于获得土地开发权的博弈中开发商具有相同的效益期望, 则可以通过以下形式进行分析:

假设三位开发商a1 ,a2 ,a3 对土地寻租的价值判定分别为

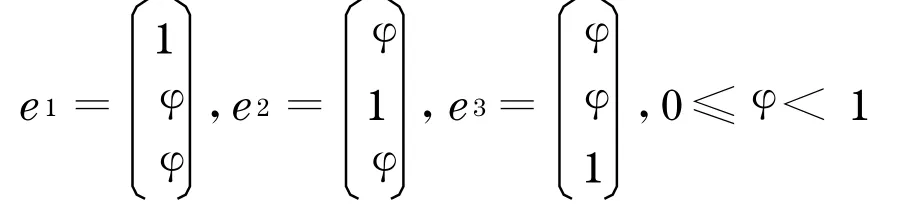
于是三位开发商的效用函数可以表达如下:

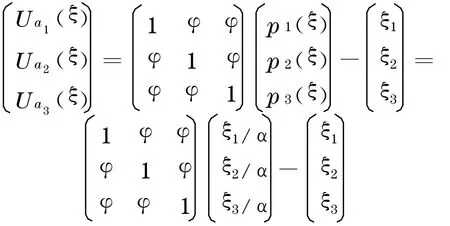
为了得到Nash 均衡解, 对U i(ξ)求偏导可得均衡条件如下:

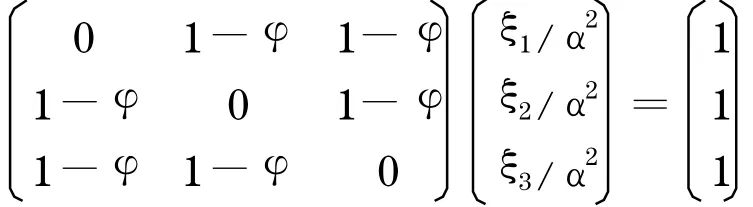
通过矩阵运算可以得到:

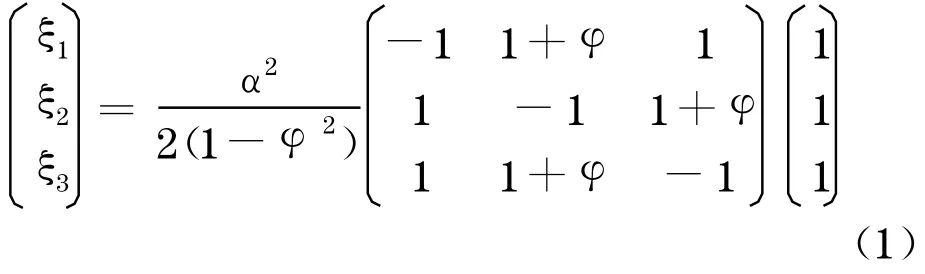
由于

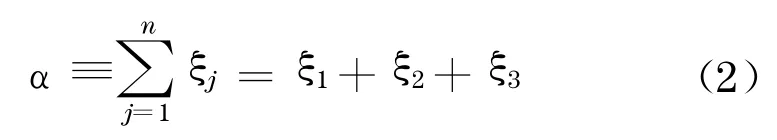
由式(1)和式(2)可求得:

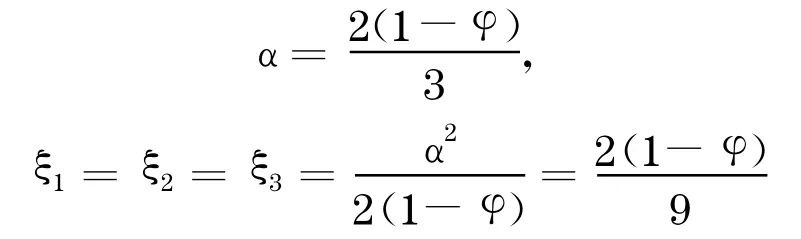
如果令φ=0 ,可以得到Tullock 最初的博弈模型,每位开发商的支付均衡为2/9,三位开发商总共的支付配置为2/3 .而在此模型中, 开发商的寻租博弈的单个支付和总体支付都下降,从dα/dφ=-2/3＜0 可以看出,开发商支付总的增长为负, 也就说开发商在相同效益期望的情况下的寻租博弈均衡总体支付下降.同时,个体支付也下降,

从均一估值的分析可以看出, 如果开发商对于土地寻租具有相同的效益期望时, 个体和总体的支付都将下降, 这将节约社会资源, 减少不必要的消耗.但从社会实际看,由于开发商个体及所处环境的差异使得这种均一估值不太可能出现, 更多的是如下所分析的差异估值情形.

2.3 差异估值分析

如果开发商对于获得土地开发权的效益期望不同,此时博弈的均衡策略将发生变化,这里还是以三家房地产开发商a1,a2,a3作为分析的对象以简化计算过程.假设a1 ,a2 ,a3 认为自己能获胜的期望值分别为:e11,e22,e33,而a1认为a2能获得开发权的期望值为φe11(0 ≤φ＜1),a2认为a1能获得开发权的期望值为φe22(0 ≤φ＜1),a3认为a1和a2获胜的期望值为零,于是便形成了不同环境下的对称寻租博弈,可以得到期望值矩阵为

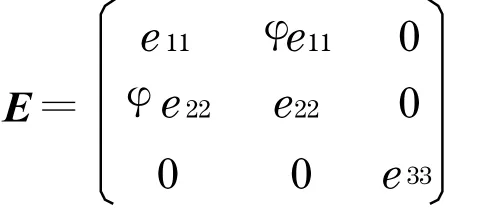
于是其效用函数可以表达如下:

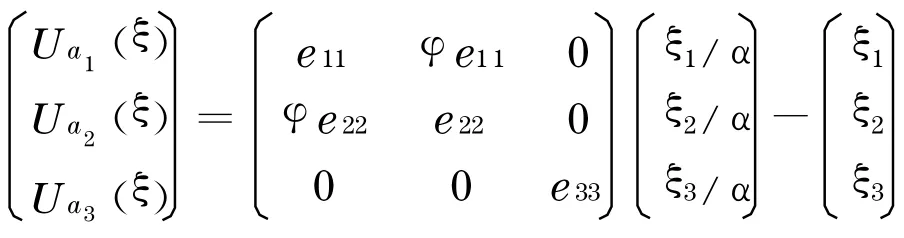
为得Nash 均衡解,对U i(ξ)求偏导得均衡解为

从式(3)～(6)可以看出, 只有所有开发商参与才能形成一个有效的均衡.若式(3)～(5)中有负值存在,则该开发商不会参与寻租博弈,所以必须确保式(3),(4),(5)为正值.在这里需要进一步分析在何种情况下开发商都会加入寻租博弈中, 这里分两种情况进行讨论:

(1)情况一:假设此时a1和a2已参与寻租博弈中, 而a3正考虑是否参与其中, 如果a3的期望的边际收益为正, 即∂U a3(ξ1,ξ2,ξ3)/∂ξ3＞0 ,a3会认为付出努力是值得的.则a3愿意参与的条件是:

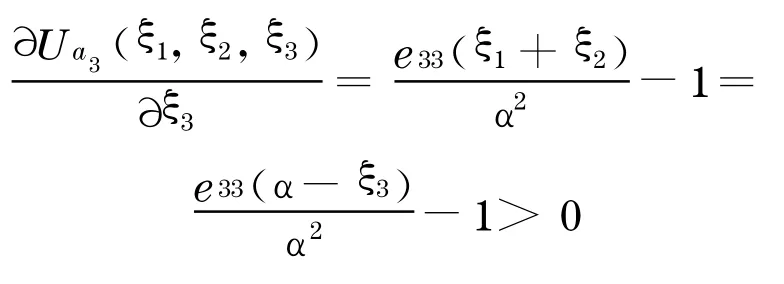
如果a3 不愿意加入博弈, 则有ξ3 =0 ,于是由式(5)有而为a1和a2博弈均衡的总期望值.在这种情况下,如果要吸引a3加入寻租博弈中来, 则必需有:e33＞,当φ=0 时,可以看出a3只有在其预期值大于a1 和a2 估值的平均值时才愿意加入.

(2)情况二:假设此时a1 和a3 已参与寻租博弈中, 而a2正考虑是否参与, 如果a2的期望的边际收益为正, 即∂U a2(ξ1,ξ2,ξ3)/∂ξ2＞0 ,a2会认为付出的努力是值得的.则a2愿意参与的条件是:

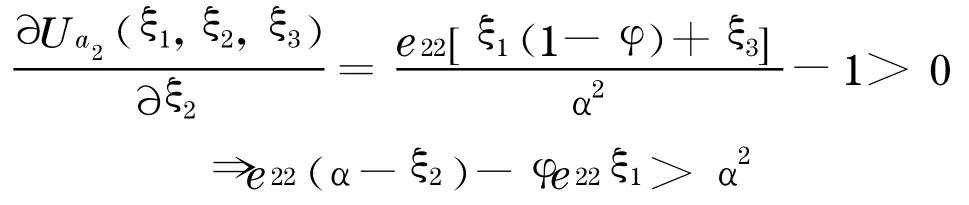
如果a2不愿意加入博弈, 则有ξ2=0 ,于是由式(4)有而为a1和a3博弈均衡的总期望值.在这种情况下, 如果要吸引a2加入寻租博弈中来, 则必需有:e22＞,当φ=0 时,可以看出a2只有在其预期值大于a1和a3估值的平均值时才愿意加入.如果a1和a3对寻租博弈的期望值有所提高, 则a2也必需提高期望值来达到加入博弈的目的.

从差异估值的分析可以看出, 当市场上存在两位开发商参与寻租博弈时, 只有当第三者对于土地价值的期望值大于前两位开发商的平均值时, 他才会愿意加入博弈.也就是说,第三者的加入受到前两位开发商期望值的约束.同理可以推广到第N位开发商的情况,其加入博弈的条件受到前N-1 位开发商的平均期望值的约束.

3 寻租博弈均衡策略

从上面的分析可以看出,a1,a2,a3对于主动参与博弈的最小期望值分别为

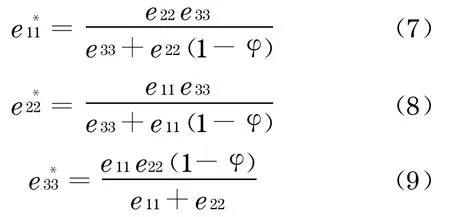
于是每位开发商的均衡策略可表示为

(1)开发商a1 的均衡策略如下:

①当eii＞e*ii,i∈{1,2 ,3}时,

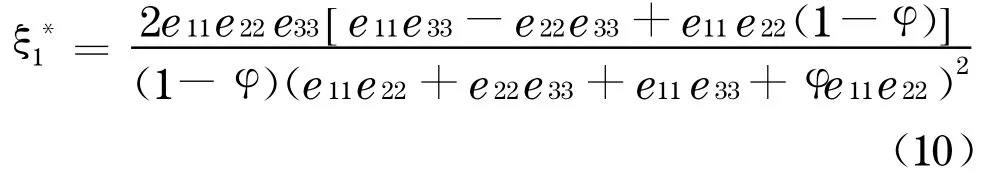
②当e22≤e2*2时,

③当e33 ≤e3*3时,

④当e11≤e1*1时, ξ1*=0 .

(2)开发商a2的均衡策略如下:

①当eii＞e*ii,i∈{1,2 ,3}时,

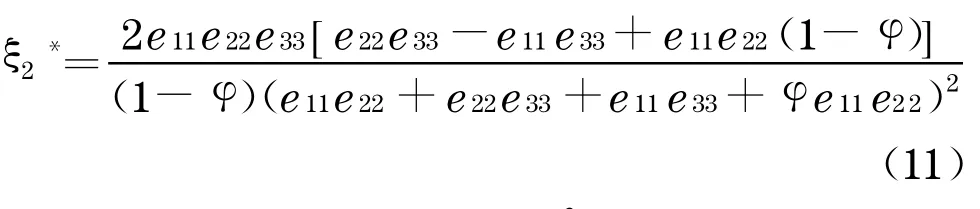
②当e11≤e1*1时,

③当e33≤e3*3时,

④当e22≤e2*2时, ξ2*=0 .

(3)开发商a3的均衡策略如下:

①当eii＞e*ii,i∈{1,2 ,3}时,

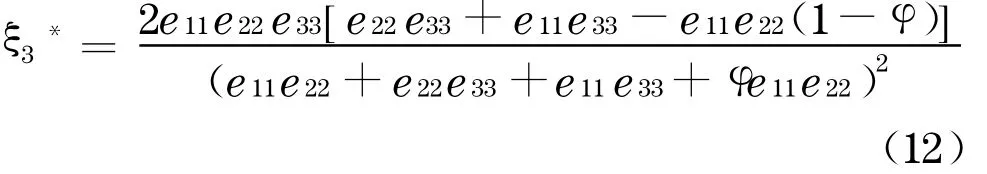
②当e11≤e1*1时,

③当e22 ≤e2*2时,

④当e33≤e3*3时, ξ3*=0 .

在此寻租博弈中,若假设所有开发商都会积极加入竞争,于是对a1,a2,a3的行动进行比较, 可以发现, 若a1和a2认为对方获胜的概率比较大,即:增大φ值, 则对于竞争中所产生的期望支付ξ*1,ξ*2,α*则会减小, 而此时a3的期望支付ξ*3则会增加.

由于:

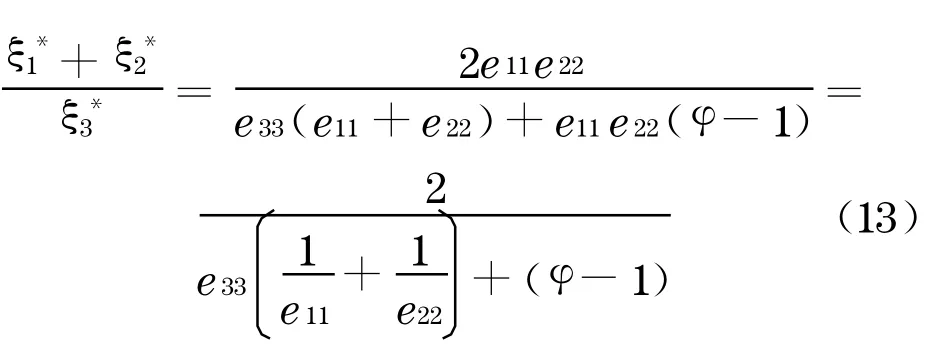
从式(13)中可以看出, ξ*1+ξ*2与e11,e22成正比,而与e33,φ成反比;而ξ*3与e11,e22成反比, 而与e33,φ成正比.

目前对寻租博弈研究的应用模型通常为古诺模型及Stackelberg 模型,古诺寻租博弈在假定租金严格为正,博弈双方对于可竞争租金具有相同估值,通过区分各自的支付函数,在一阶效用最大化条件下完成古诺均衡的策略选择,而Stackelberg 寻租博弈中的博弈双方对于租金拥有不对称估值,通过比较无差异曲线的斜率发现,率先行动者将可能有一个更高的期望支付.相比之下,Stackelberg 模型对于不完全信息条件下的寻租博弈分析具有更为重要的现实意义.本文所使用的方法则是基于Stackelberg 寻租博弈思想的延伸,在拓展Tullock 模型的基础上,基于土地开发的不同效益期望, 得到了寻租博弈的有效均衡策略, 通过改变φ值可以实现寻租博弈均衡的转移, 从而有选择地引导博弈均衡策略的实现.

4 实例分析

假设一个区域内有三家房地产开发商a1,a2,a3,他们认为自己能获胜的期望值分别为:e11=6 ,e22=8 ,e33=10 ,而a1认为a2能获得开发权的期望值为φe11=0 .5 ×6 =3(φ=0 .5),a2认为a1能获得开发权的期望值为φe22=0 .5 ×8 =4(φ=0 .5),a3认为a1和a2获胜的期望值为零, 于是便形成了不同环境下的对称寻租博弈, 可以得到期望值矩阵为

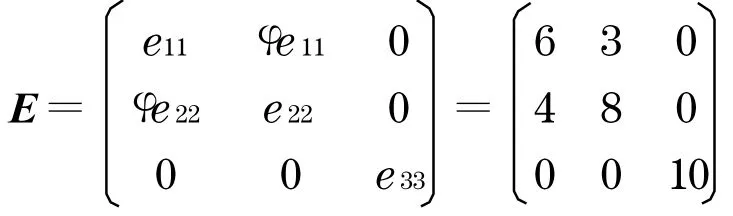
由式(7)～(9)可得:

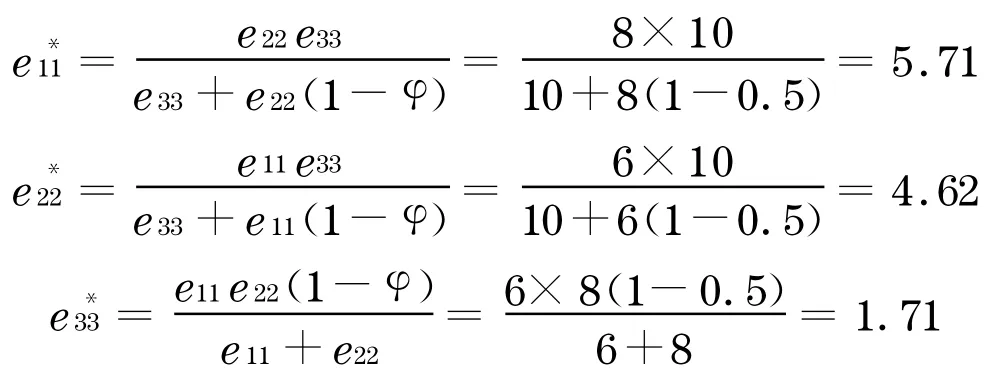
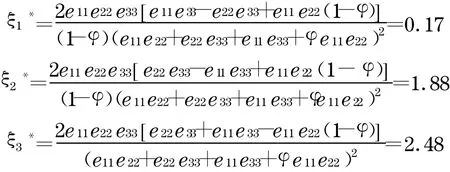
由以上计算可知:在a1 ,a2 ,a3组成的开发商中,a1,a2,a3都会积极地加入寻租博弈中来,而a1的期望支付最小,a3的期望支付最大, ξ*3＞ξ*2＞ξ*1,由可知:在同等期望支付的条件下,a3获胜的概率较小,而a1获胜的概率较大.

接下来改变φ值,博弈的均衡策略将发生重大变化.假设开发商a1存在诚信问题,而开发商a2对社会的贡献较突出,此时希望寻租博弈均衡向a2倾斜, 则可增大φ值,取φ=0 .8 ,期望值矩阵变化如下:

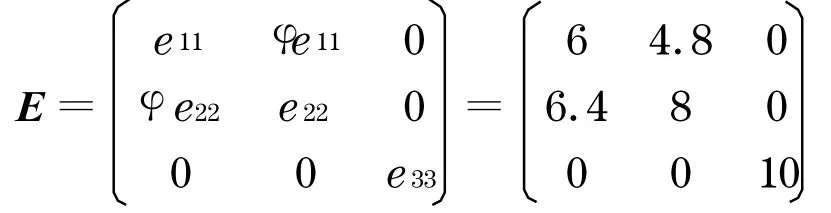
由式(7)～(9)可得:e*11=6 .90 ,e*22=5 .36 ,e*33=0 .69.由于,e11≤e*11,由前面第3 节的分析可知:ξ*1=0 ;.可以看出,在该寻租博弈中实际的支付总值ξ*1+ξ*2+ξ*3下降了,社会资源得到节约.由于开发商a1的实际期望值达不到参与博弈的最小期望值,即:e11≤e*11,故a1将淡出寻租竞争,而在开发商a2与a3的竞争中,ξ*2＜ξ*3,故在同等期望支付的条件下,a3获胜的概率较小,而a2获胜的概率较大.可见,通过增大φ值,使寻租博弈的均衡策略发生转移,有利于社会公平的实现.

5 结论

在房地产领域,开发商以自身利益最大化为目标,为获取土地的开发权而实施寻租,开发商的寻租行为会带来利益竞争,损害社会公平,最终会将寻租成本传递到房地产的市场定价上.本文在经典Tullock 寻租博弈模型的基础上,考虑到开发商对于土地价值期望的不同,利用期望矩阵扩展了寻租博弈的应用范围.并分析了均一估值和差异估值下的博弈均衡的变化,得到了寻租博弈的有效均衡策略.该模型是对房地产开发商土地寻租博弈的有益尝试,可以预测博弈的结果,通过改变φ值可以改变寻租博弈的均衡,从而有选择地引导博弈均衡策略向有利于社会公平方向转移.

[1] Tullock G .Efficient rent-seeking :toward a theory of the rentseeking society [M] .[S .l .] :Tex as A & MUniversity Press, 1980.

[2] Perez-Castrillo J D, Verdier T .A general analy sis of rentseeking games[J] .Public Choice,1992, 73(3):335.

[3] Bruce G L .Stackelberg rent-seeking[J] .Public Choice, 1993,77(2):307.

[4] Bruce G L .Cooperative rent-seeking[J] .Public Choice, 1994,81(1-2):23.

[5] Skaperdas S,Gan L.Risk aversion in contests [J] .The Economic Journal, 1995, 105:951.

[6] Szidarovszky F, Okuguchi K .On the existence and uniqueness of pure Nash equilibrium in rent-seeking games[J] .Gam es and Economic Behavior,1997, 18(1):135.

[7] William E S .Asymmetric rent-seeking with more than two contestants[J] .Public Choice, 2002, 113(3-4):325.

[8] Cornes R, Hartley R.Risk aversion, heterogeneity and contests[J] .Public Choice,2003, 117(1-2):1.

[9] David A M, Andrew J Y .Equilibria in rent-seeking contests with homogeneous success functions[J] .Economic Theory ,2006, 27(3):719.

[10] Matros A .Rent-seeking with asymmetric valuations:addition or deletion of a player [J] .Public Choice, 2006, 129(3-4):369.

[11] Riechmann T .An analy sis of rent-seeking games with relativepayoff maximizers[J] .Public Choice, 2007, 133(1-2):147.

[12] Yamazaki T . The uniqueness of pure-strategy Nash equilibrium in rent-seeking games with risk-averse players[J] .Public Choice, 2009, 139(3-4):335.

[13] Yamazaki T .On the existence and uniqueness of pure-strategy Nash equilibrium in asymmetric rent-seeking contests[J] .Journal of Public Economic Theory,2008, 10:317.

[14] Matros A,Armanios D . Tullock ' s contest with reimbursements[J] .Public Choice,2009, 141(1-2):49.

[15] Schoonbeek L .Bribing potential entrants in a rent-seeking contest[J] .Public Choice, 2009, 139(1-2):153.

[16] 王斌, 徐寅峰, 李志敏.寻租现象监督治理的不完全信息动态博弈分析[J] .系统工程, 2005, 23(10):81.WANG Bin, XU Yinfeng,LI Zhimin .A dynamic game analysis on disposal of rent-seeking phenomina with incomplete information[J] .Systems Engineering,2005, 23(10):81.

[17] 华武, 缪柏其.战略联盟寻租博弈分析[J] .中国管理科学,2002, 10(3):18.H UA Wu,MIAO Baiqi .Analysis on stackelberg rent-seeking games in the strategic alliance [J] .Chinese Journal of Management Science,2002, 10(3):18.

[18] David A M, Andrew J Y .Equilibria in rent-seeking contests with homogeneous success functions[J] .Economic Theory ,2006, 27(3):719.

[19] Skaperdas S .Contest success functions[J] .Economic Theory ,1996, 7(2):283.