旋转飞行器固体火箭发动机非稳态气流作用分析

郜 冶,刘平安,杨 丹

(哈尔滨工程大学航天工程系,哈尔滨150001)

0 引 言

早在上世纪六十年代美国对某卫星第三级旋转发动机飞行的测量中[1],已了解到角加速度引起的章动现象,由于当时发动机尺寸较小,并未出现章动摇摆的剧烈增长情况。八十年代,在美国Star-48旋转固体火箭发动机[2-3]搭载卫星的过程中,发现了严重的飞行器不规则圆锥运动,即章动现象,这一现象足以导致发射任务失败。后来,我国在小卫星发射的过程中遇到同样的问题。从出现章动角度放大的PAM(Payload Assist Module)-D系列飞行器的测试结果[2](见图1)中可以发现,飞行器的不规则进动与固体火箭发动机的工作情况有关,图中可以看到,从发动机点火至工作57秒,飞行器均处于小角度脉动状态,侧向角速度不超过3 Deg/s。随后章动角速度在75秒开始大幅度增长,在88秒燃烧结束时达到最大值,并突然停止增大。许多学者[4-8]开始从很多方面对这一现象进行细致全面的分析研究。大部分研究者认为,由于喷气阻尼(Jet damping)的作用,在初始条件下产生的使飞行器发生摇摆的侧向力或侧向角速度会随时间被逐渐耗散,直至减小为零,这样发动机的运动会逐渐趋于稳定。

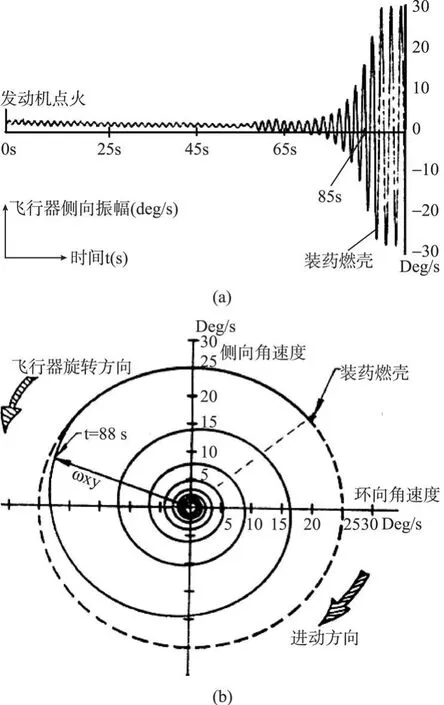
图1 PAM-D的遥测结果Fig.1 Pitch rate citefrom PAM-Dflights

经典的喷气阻尼定义是由 Rosser、Newton、Gross[4]首先给出的,但在当时(1947年)这一理论就存在一些尚未解决的问题,如小型战术火箭的飞行试验观测与理论计算结果相矛盾的情况,这些问题一直没有得到解决,而传统的喷气阻尼理论仍然被广泛使用[1,7-8]。大部分参考这一理论的分析都是建立在“准稳态”流动假设基础上的,并假设流场内的流动是平行于对称轴的,然而用于分析飞行器发生章动不稳定性的最大误差来源于第一种假设,准稳态近似的假设,即假设不存在非稳态扰动力矩作用,而此时即使是在章动不稳定条件下,扰动力矩的作用仍然为零。本文的主要目的就是分析在某些特定条件下,存在非稳态力矩作用的情况下,是否会使各种非稳态力矩的相互作用效果超过喷气阻尼作用,而产生章动不稳定性运动。

1 数学模型

气动力矩作用是由飞行器系统内燃气流的相对运动引起的,因此这里对由气流相对运动产生的力矩进行分析,则有[2]:

将气流速度与旋转角速度分解为平均流与波动(非稳态)项和的形式,即:

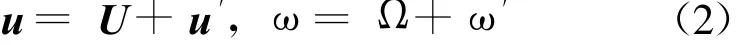
式中 U表示速度矢量的平均值,Ω为飞行器角速度矢量的稳态部分,u′、ω′为非稳态的速度和角速度矢量,与平均量相比,u′、ω′可假设为小量。这一假设可通过实际飞行测量的数据得到证明,飞行器的旋转角速度为5.26 rad/s,而章动角速度的最大值约为0.5 rad/s,可见章动不稳定性的最大幅值小于飞行器自旋角速度的10%。

将式(2)代入式(1)中,并将平均项与波动项分解,可得到表1中所示的飞行器与内部气流相互作用的力矩。Group1表示在燃烧室内产生的二次流动引起的稳态力矩,例如,结合哥氏力的容积积分和角动量对流的轴向、径向面积积分,产生的与燃气流动相重叠的轴向涡流作用。Group2表示飞行器角运动的非稳态作用与发动机燃烧室内的稳态流动之间的相互作用。这一容积积分项中包含了哥氏加速度(2ω′×U),它正是产生经典的喷气阻尼作用的源项。若喷气阻尼力矩项与产生章动不稳定性的扰动力矩具有相同的量级,但方向相反,那么就会使飞行器产生实际飞行中观测到的侧向角运动被逐渐放大的情况。Group3、Group4表示燃烧室内气流速度的非稳态部分与稳态平均流动以及飞行器平均自旋运动之间的相互作用,而燃气流的非稳态流动项是由发动机燃烧室壁面的非稳态刚体角运动激发出来的。这些相互作用力矩的一阶形式由哥氏力和加速度项的体积积分表示,以及对流作用的面积积分。用于描述扰动角动量对流作用的面积积分项具有重要的影响,它是由平均气流流动流出发动机喷管出口产生的。Group5中的高阶项没有进行展开,他们是由 u′、ω′构成的二阶非线性项作用,因此与一阶项相比可忽略不计。

1.1 喷气阻尼作用

喷气阻尼力矩由Group2中的哥氏力积分作用项表示,有:

以图2所示的飞行器系统为模型,用于求解喷气阻尼力矩作用的大小。

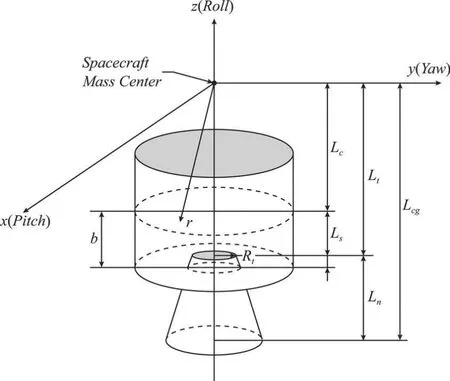
图2 发动机燃烧室及喷管几何构形Fig.2 Motor chamber and nozzle geometry

图2 所示的飞行器模型中,发动机内装药为柱形,燃烧方式为端面与内管同时燃烧,并假设发动机的流量是以线性方式增大的,则喷气阻尼力矩可表示为[2]:

其中:Lcg为喷管出口相对于飞行器质心的距离m;Ln为喷管长度,m;2b为发动机燃烧室的长度,m。

表1 飞行器与内部气流相互作用产生的作用于飞行器上的力矩Table 1 Moment on spacecraft due to interaction with internal flow field

这里:Group 1为稳态流动作用;Group 2为喷气阻尼力矩;Group 3为非稳态流动作用;Group 4为角动量的非稳态对流作用;Group 5为非线性作用项(高阶小量)。U是包括轴向涡流分量在内的平均流速度矢量,Ω是沿发动机对称轴方向的飞行器主自旋角速度矢量。u′是由于燃烧室的章动运动产生的非稳态的气流速度波动,ω′是章动角速度,即侧向角速度。r是相对于飞行器质心的发动机燃烧室或者喷管内任意一点的位置矢量,n为控制容积表面的单位面积矢量。系统的控制容积包括飞行器负载和固体火箭发动机部分,燃气流由喷管尾部喷出控制容积系统。

KJ为喷气阻尼系数,表示MJ相对于角速度波动矢量ω′的比值,则有:

由上式可知,KJ为负值。按照Rosser的定义喷气阻尼力矩的结果可表示为K J=-˙m(L2cg),也就是说经典的喷气阻尼理论在某种程度上夸大了喷气阻尼力矩的作用。

由式(4)可知,喷气阻尼力矩与角速度矢量振荡的方向刚好相反,也就是说喷气阻尼力矩的作用效果是阻止飞行器的侧向角运动。随着发动机装药的燃烧,系统质心向前移动,燃烧室长度增加,喷气阻尼系数KJ的大小也随之增大。

Flandro[2]指出,旋转发动机内存在由燃烧室头部延伸至喷管的轴向涡核流动。这一现象在很多旋转固体火箭发动机中均被忽略掉。发动机内气流经由喷管加速以及推进剂表面燃烧气流注入产生了涡核的延伸,最终形成了涡核流动,涡核的延伸不仅会影响喷管流动,还会使燃烧室压力以及推进剂的燃烧速度与之发生响应,而产生波动现象。

1.2 非稳态流动作用

表1中Group3、Group4是杉烧产物中与时间相关的气流速度振荡与燃烧室旋转和平均流动之间的相互作用产生的飞行器内部作用力矩。旋转发动机内的平均流动是比较复杂的,且由于轴向涡核流动的存在,使得这些非稳态力矩作用更加复杂,难以确定。

Group3的第一项是与喷气阻尼项近似的由哥氏加速度产生的作用,第二项为燃烧室内角动量的时间变化率。Group4为流出燃烧室的平均流和波动速度的对流,喷管出口处的这两项积分结合起来表示侧向非稳态角动量的对流作用,并且产生了一个重要的作用于飞行器上的扰动力矩。

Group4第二项的反作用力矩可表示为:

上式在喷管出口的积分表示由平均流动带走的系统角动量随时间变化的通量,这一通量是由速度振荡u′引起的,而 u′是燃烧室内气流响应飞行器非稳态角运动,即刚体摆动产生的,且飞行器同时还存在自旋运动。

表示容积d V中气流角动量的振荡分量。

图3所示为平均流流经燃烧室并流出喷管的延伸情况,其中 U为平均流速度,u′为速度波动,垂直于 U。图中给出了气流角动量分量d H随时间的变化,由于系统角动量守恒,因此随着气流接近系统轴线,角动量的大小逐渐增大。气流速度波动产生的侧向角动量分量反作用于飞行器,产生了扰动力矩作用。如图中所示,若力矩项 M H平行于角速度分量ω′,且其大小与喷气阻尼力矩M J相当,则章动不稳定性就会随时间而增大。

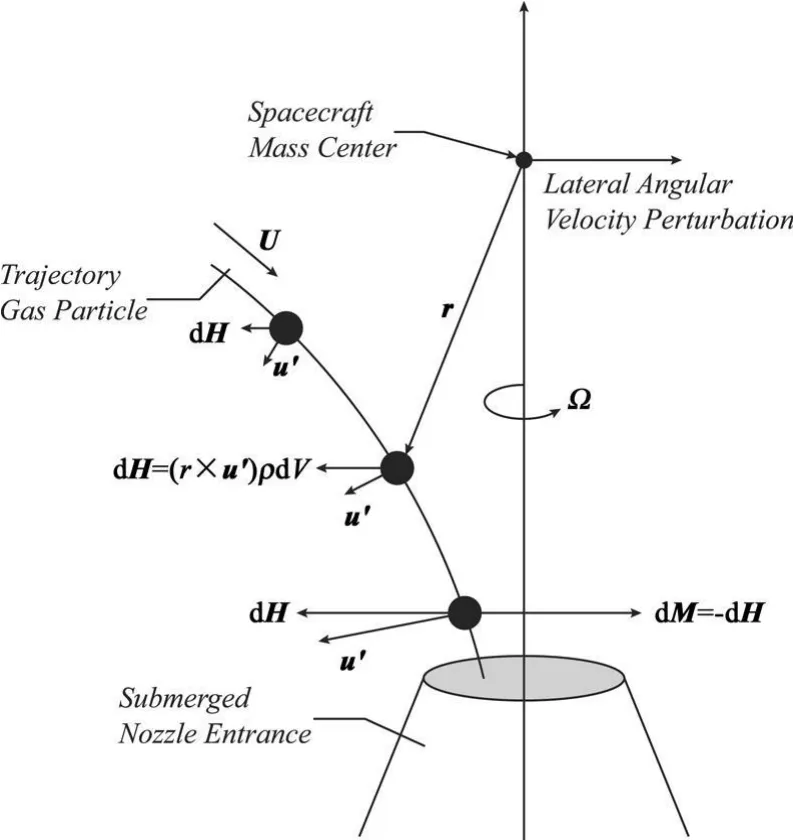
图3 气流侧向转动惯量微团的延伸Fig.3 Stretching of the lateral angular momentum of particle

上文对旋转火箭内的气流流动进行了分析,并得到非稳态作用项的存在,表1中Group3、Group4产生的作用于飞行器上的反作用力矩,使得飞行器发生章动不稳定性,那么要得到这些非稳态项对飞行器运动以及章动不稳定性的影响程度,就需要得到这些非稳态作用的具体形式。Group3、Group4中的各项都与非稳态速度 u′有关,因此Flandro在研究中利用惯性波理论对u′进行了傅里叶展开,并将结果代入到非稳态作用项中,得到了气流扰动力矩项的矢量表达方式:

这里下标表示Group3、Group4中的各项,如M31表示Group3的第一项,其中有:

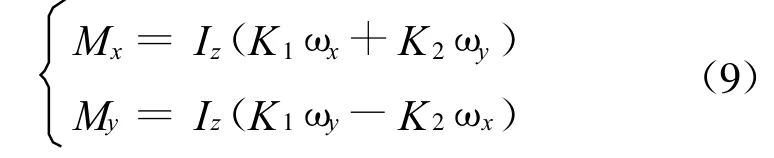
其中系数K1、K2为傅里叶展开的系数合并项,其表达方式十分复杂,用于描述非稳态涡流特性,K 1、K 2的单位为s-1。

由式(9)可知气流扰动力矩MH与章动角速度波动成比例,MH的物理意义是气流相对于飞行器摆动的线性响应,飞行器与火箭发动机内的燃气流组成了一个封闭的循环系统,即自激振荡系统。

图4所示为M H相对于M J和角速度振荡分量ω′的方位角,MH的幅值和相角φ相对于ω′可表示为K1、K2的函数 :

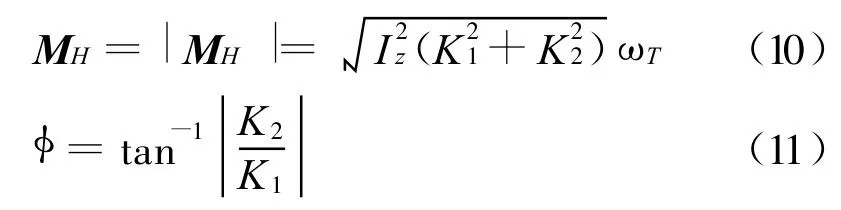
这里 ωT为侧向加速度,即角速度的振荡分量 ω′。

图4 扰动力矩相对于章动角速度的方位角Fig.4 Orientation of disturbing moment relative to nutation angular velocity

将前文对气动力矩项的分析引入到描述飞行器系统姿态运动的欧拉方程中,就可以得到非稳态力矩项对飞行器整体姿态运动的影响程度,由于K 1、K2的表示涉及较多的复杂参数,因此这里仅将K1、K2作为恒值代入,则有[9]:

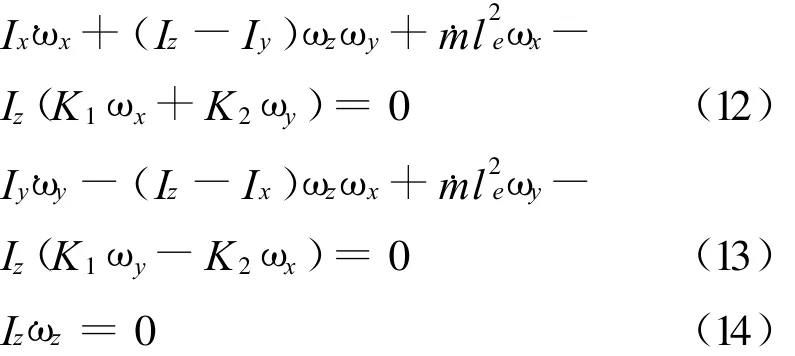
将式(12)和(13)合并后有:

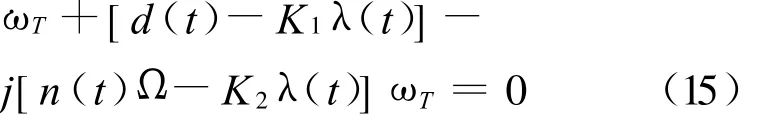
则随装药的燃烧,侧向角速度 ωT可表示为:

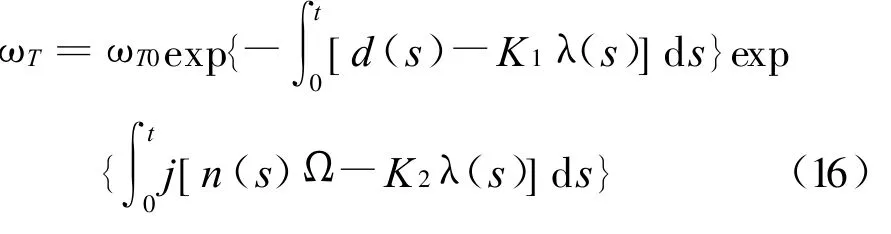
令:

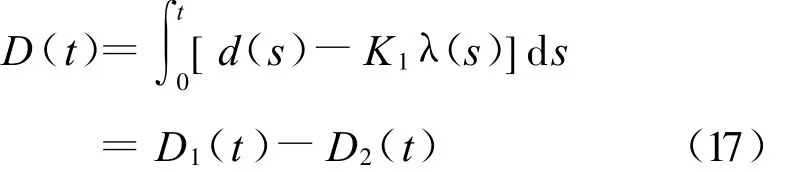
则有:

这里将喷气阻尼作用与非稳态气流作用的积分函数分别用D1(t)、D2(t)表示,这两个函数共同作用决定了侧向角速度的幅值,这里将D1(t)、D2(t)简称为幅值函数。

飞行器章动角度:

体章动角度:

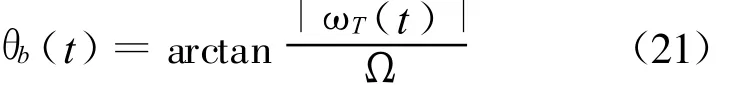
2 算例与结果分析

下面就采用式(15)的系统模型,对两种不同飞行器算例进行发动机工作条件下的系统姿态运动的计算。

2.1 柱形燃烧室发动机算例

首先对简化的柱形燃烧室及装药变化的飞行器参数系统进行欧拉方程的求解,令飞行器的初始侧向角速度为ωT0=1.0deg/s(约为0.0174533 rad/s),且K1为恒值,计算中所关心的是章动幅度的变化,对章动频率的影响假设为恒值,即K2=2.5(下同),此时系统章动周期约为1.7 s。

图5 K 1=0.275时柱形燃烧室发动机飞行器的章动角度Fig.5 Nutation angle of the spacecraftwith cylindrical chamber when K1=0.275

图5 -6为K1=0.275时系统章动幅度随时间的变化,章动角度在K1为恒值时,在发动机工作初始已经开始增长,在接近40 s时达到最高值0.0982 rad(约为5.62702 deg)。侧向角速度的变化与章动角度相同,最大值达到约0.25301 rad/s(约14.4964 deg/s)。由飞行器幅值函数的相对值之间的变化,图7中可以看出,产生章动增长的原因是在40 s之前,非稳态气流作用力矩的增长速度超过了喷气阻尼力矩的增长速度,使得此时非稳态项占主导地位,但随着装药的燃烧,发动机流量逐渐增大,飞行器质心前移,使得喷气阻尼力矩的增大速度逐渐超过了非稳态气流作用力矩,因此章动幅度又逐渐减小,在发动机工作结束时减小为零。

图6 K 1=0.275时侧向角速度Fig.6 Lateral angular velocity when K 1=0.275

图7 K 1=0.275时幅值函数的作用效果Fig.7 Effects of the amplitudefunctions when K 1=0.275

由飞行器的实际观测数据已经得知,飞行器的章动增长并不是在发动机工作初始就开始的,而是在发动机工作中期逐渐开始的,因此K 1并不仅仅为恒值,这里先假设K1为时间的函数,并将K1为时间的一阶、二阶函数代入欧拉模型方程进行计算。

图8-9为K1=0.0053t时章动幅度的变化,这里K 1的取值标准为使章动角度的波动范围在0.1 rad以内,以便对不同形式的K1值进行比较。由图中可知,当K 1为时间的一阶函数时,章动角度在发动机工作初始增长缓慢,最高值仍约为0.1 rad,而其达到最高值的时间相对于K1=0.275时后移,此时侧向章动角速度的极值也向后移动,且所达到的最高值与K 1=0.275时接近。章动角度与侧向角速度的这种对应关系是由系统参数所决定的。

图8 K 1=0.0053t时柱形燃烧室发动机飞行器的章动角度Fig.8 Nutation angle of the spacecraftwith cylindrical chamber when K1=0.0053t

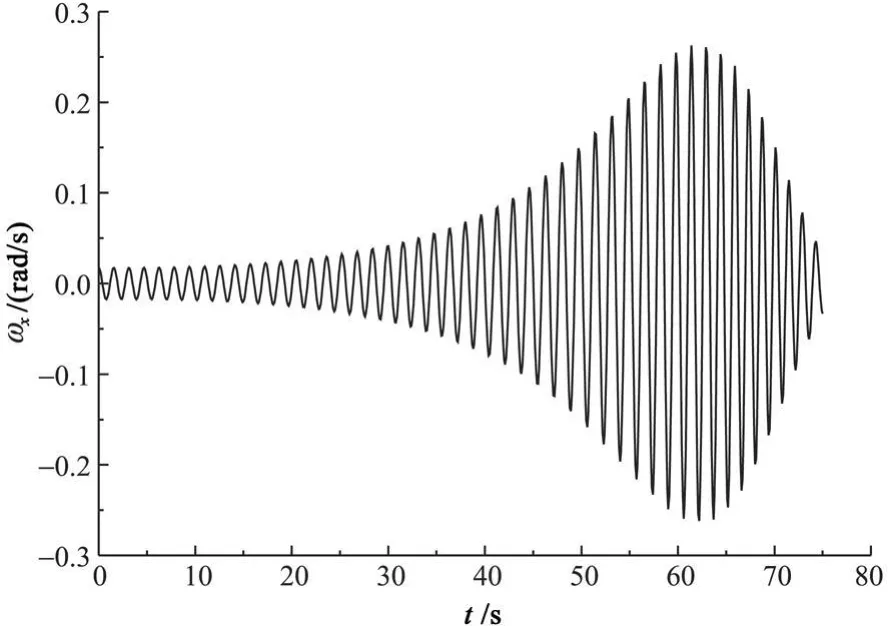
图9 K 1=0.0053t时侧向角速度Fig.9 Lateral angular velocity when K 1=0.0053t

由图10的幅值函数曲线可知,K1为时间的一阶函数条件下,非稳态气流作用力矩初始的增长幅度较慢,而后逐渐增大,但在发动机工作临近结束时,喷气阻尼力矩的增长速度较快,因此章动幅度又开始减弱。

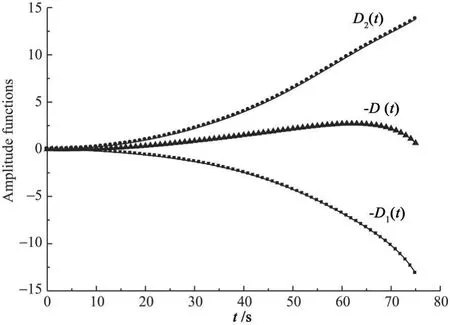
图10 K 1=0.0053t时幅值函数的作用效果Fig.10 Effects of the amplitude functions when K1=0.0053t

图11 -12所示为K1取时间的二阶函数时,系统章动幅度的变化,可知当K 1=8.0×10-5t2时,章动角度在发动机工作前半段有小幅度减弱,而后在发动机工作40 s-50 s开始大幅度增长,到了约70 s时达到最高点,最后又迅速减小,在发动机停止工作时其幅值仍较大。侧向角速度的变化也是如此,这一变化过程与实际当中飞行器的姿态运动情况十分相似,只是实际情况中在发动机工作末期章动角度并没有减小,且在发动机工作结束后,仍保持一定的章动幅度。

通过对K1分别为恒值和时间的一阶、二阶函数的情况下的计算可知,随着K1值的增大,章动角度的最高幅度也增大,且时间后移,K1的不同取值形式决定了非稳态作用力矩的变化趋势,且当K1为时间的二阶函数时与实际运动的章动不稳定性情况最接近。

Flandro[2]利用惯性波动理论对非稳态项进行傅里叶展开,并利用飞行器参数对WESTAR-V飞行器的非稳态扰动力矩项进行了求解,得到 δK1的取值范围为0～1.0×10-4,δ为力矩比例参数,可表示为:

δ的量级约为2.0×10-4,那么K1的取值范围约为0.5,这与本文中对K1的取值范围量级相同,可见本文对K1的取值是合理的。由此证明了在某些飞行器参数条件下,发动机内部气流流动产生了非稳态气流作用力矩,这一扰动力矩与喷气阻尼力矩同量级,该力矩就是产生飞行器章动不稳定性的源项。

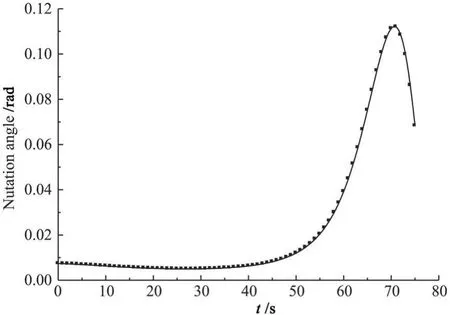
图11 K1=8.0×10-5 t 2时柱形燃烧室发动机飞行器的章动角度Fig.11 Nutation angle of the spacecraftwith cylindrical chamber when K1=8.0×10-5 t2

图12 K1=8.0×10-5 t 2时侧向角速度Fig.12 Lateral angular velocity when K 1=8.0×10-5 t2

实际情况中发生章动不稳定性的飞行器,在发动机工作前半段章动幅度几乎没有波动,到了约40 s-50 s开始增长,在发动机工作结束时增长停止,且维持不变。飞行器最大章动角度约0.27 rad(约15.46986 deg/s),侧向角速度最高为 25 deg/s(约0.43633 rad/s)。前半段的无波动并不代表扰动力矩的作用为零,只能是扰动力矩的作用还未超过喷气阻尼力矩,而在发动机工作接近结束时,扰动力矩已经增大到超过了喷气阻尼力矩,从而产生了章动幅度达到了最高值。这一现象与前面对涡核延伸的假设相互吻合,涡核流动是由气流逐渐注入产生的,且在发动机工作结束段,发动机燃烧室内空间增大的条件下,涡核流动的作用空间也不断增大,就使得扰动力矩持续增强,而同时喷气阻尼作用力矩是与发动机内尺寸变化不相关的。

2.2 STAR 48发动机算例

STAR 48发动机飞行器同样令其初始侧向角速度为1 deg/s,K2取恒值,即K2=0.5,得到的频率尺度与算例1接近,章动周期约为2.0 s。

图13为K1=0.20时侧向角速度的变化,由图中可知,侧向角速度在发动机工作初始已经开始增长,这与算例1在K1取恒值时的情况相同,在发动机工作40 s-50 s时章动角度有小幅度减弱,在发动机工作结束段又开始增加,这主要是由于产生STAR 48发动机喷气阻尼力矩的飞行器参数决定的,且由图14中幅值函数的相对值也可以看出,喷气阻尼函数的变化范围比算例1小约1倍,且此时喷气阻尼力矩的增长速度变化很小,与K 1为恒值的扰动力矩项几乎为对称关系,从而使得章动角度随之发生小幅波动。

图13 K 1=0.20时STAR 48发动机飞行器的侧向角速度Fig.13 Lateral angular velocity of the spacecraft with STAR 48 when K 1=0.20

图15 为K1=2.75×10-3t时章动角速度的变化,由于非稳态作用力矩的增长速度有所减慢,章动幅度初始有缓慢减小,随后在t=50-60 s开始逐渐增大,直至燃烧结束。此时章动角度增大到约0.1 rad,侧向角速度只增加到0.11921 rad/s(约6.83023 deg/s),也就是说由于飞行器转动惯量的分布不同,产生与算例1相同的侧向角速度,会得到更大的章动角度。

经过对比可以发现,STAR 48发动机的非稳态力矩作用为时间的一阶函数时,产生的章动不稳定性与实际较接近。

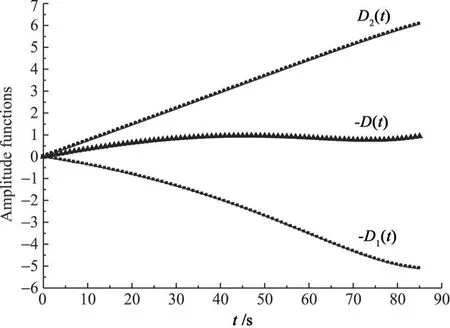
图14 K1=0.20时幅值函数的作用效果Fig.14 Effects of the amplitude functionswhen K 1=0.20

随着燃烧的进行,燃烧室内的流动空间逐渐增大,燃气流流出燃烧室的路径变长,那么气流在燃烧室内的停留时间便会增长,加上气流的不断注入,使得涡核流动的强度不断增加,扰动力矩也逐渐增强。在发动机工作即将结束时,扰动力矩的增长速度迅速增大,逐渐超过了喷气阻尼力矩。我们可以认为,若发动机在扰动力矩没有迅速增大之前就停止工作,那么章动幅度就不会增大到使飞行器失稳的程度。

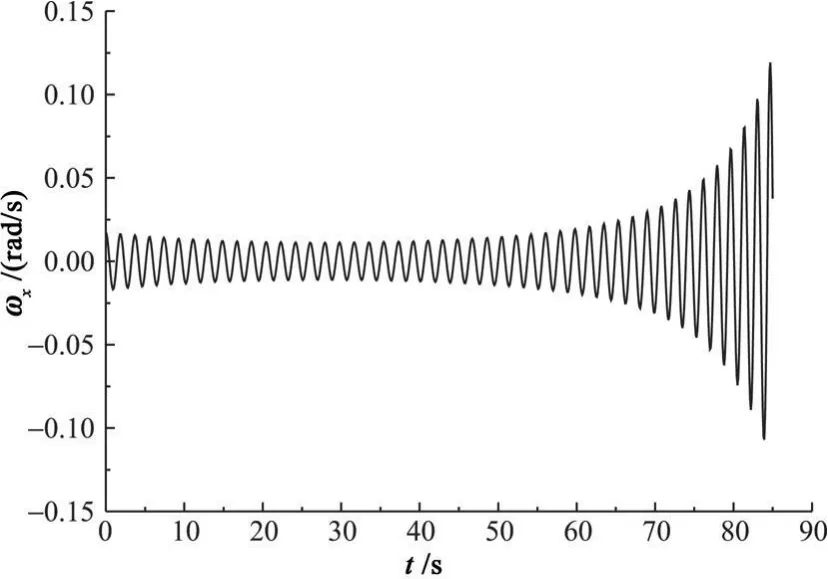
图15 K 1=2.75×10-3 t时STAR 48发动机飞行器的侧向角速度Fig.15 Lateral angular velocity of the spacecraft with STAR 48when K 1=2.75×10-3 t

由此可知,在以往对某些同类型自旋稳定飞行器的测试中,未发现章动角度增大的现象发生,并不能说明这些系统就是稳定的,而是由于各参数的综合作用,使得在发动机工作结束时,章动不稳定性还没有被放大到致使系统不稳定的程度。

4 结 论

本文在飞行器运动方程的基础上,引入Flandro的非稳态气流作用力矩模型,对实际的飞行器参数进行了计算,结果显示非稳态气流产生的侧向扰动力矩是飞行器发生非稳态圆锥运动的主要因素。当扰动力矩的作用逐渐超过了喷气阻尼力矩时,就会出现章动现象。当发动机在扰动力矩没有迅速增大之前就停止工作,那么章动幅度就不会增大到使飞行器失稳的程度。但是发动机内流场的气流作用是十分复杂的,要得到气流非稳态作用的产生机理,就需要对发动机三维非稳态内流场进行深入研究。

[1] Rott N,Pottsepp L.Simplified calculation of jet-damping effects[J].AIAA Journal,1964,2(4):764-766.

[2] Flandro GA,VanMoorhem WK,Shoethill R,et al.Fluid mechanics of spinning rockets[R].AFRPL TR-86-072,AD-A177350,1987:9-35.

[3] Yam Y,Mingori D L,Halsmer DM.Stability of a spinning axisymmetric rocket with dissipative internal mass motion[J].Journal of Guidance Control and Dynamics,1997,20(2):306-312.

[4] Rosser J B,Newton RRand GrossG L.Mathematical theory of rocket flight[M].New York:McGraw-Hill Book Company,Inc,1947:20.

[5] 郜冶,杨丹,熊永亮.旋转飞行器固体火箭发动机引起的章动不稳定性分析[J].宇航学报,2008,29(1):270-275.[GAO Ye,YANG Dan,XIONG Yong-liang.Coning instability analysis of spinning solid rocket motor[J].Journal of Astronautics,2008,29(1):270-275.]

[6] 杨丹,郜冶,熊永亮.旋转固体火箭发动机随质量变化的姿态运动分析[J].推进技术,2008,29(1):8-12.[YANG Dan,GAO Ye,XIONG Yong-liang.Preliminary analysis of spinning solid rocketmotor dynamicsstability[J].Journal of Propulsion Technology,2008,29(1):8-12.]

[7] Breuer D W,Southerland W R.Jet-damping effects:theory and experiment[J].Journal of Spacecraft and Rocket,1965,2(4):638-639.

[8] Thomson WT,Reiter GS.Jet damping of a solid rocket:theory and flight results[J].AIAA Journal,1965,3(3):413-417.

[9] Janssens F.Jet damping and nutation growth during the burn of a solid rocket motor such as PAM-D[J].ESA Journal,1988,12:273-288.