基于三目视觉测量的航天器交会对接相对位姿确定算法
钱 萍,王惠南
(南京航空航天大学航天学院,南京 210016)
0 引 言
RVD测量技术是空间交会对接中一项十分重要的关键技术[1]。目前国内外研究的主要方法有GPS导航、微波雷达、红外跟踪、以及以CCD相机为光学成像敏感器的计算机视觉测量方法等。采用CCD光学成像方法来实现两航天器(目标器、追踪器)间相对位姿参数的测量,即在追踪器上安装CCD相机,在目标航天器上安装几何形状及尺寸已知的特征点,通过对特征点在CCD上成像的分析和计算就可以确定两航天器的相对位置和姿态[2]。国内外学者对这方面已经做了大量研究[3-4],其中最传统的方法是利用单CCD进行测量。然而,由于这种算法的基本方程为二次非线性方程,无直接解析解,需迭代求数值解,因此迭代求解的收敛性和速度将极大影响测量的实时性和准确性[5]。所以近年来人们提出双目视觉的测量方法,其基本方程为线性方程,存在解析解,所以计算过程简单,测量精度高,故理论上该模型优于单摄像机的模型。但双目视觉测量在工程应用中存在一个重要技术难点,即图像的匹配问题。有研究表明,在摄像机标定的情况下,特征像点的定位匹配误差是引起位置测量误差的主要原因。而两航天器的相对姿态是通过特征点的空间位置来确定的,因此姿态误差最终也归咎于特征像点的定位匹配误差[5]。为解决上述问题,本文提出利用三目视觉的方法来测量两航天器间的相对位姿参数,既避免了单目测量中需要迭代求解二次非线性方程的实时性、准确性及收敛性问题,又有效地减小了双目测量中因图像匹配而带来的定位误差与姿态误差。除此之外,三目测量亦是一种冗余度技术,使测量系统更加安全可靠,这在航天技术应用中自然是一个首要问题。
1 三目视觉相对位姿确定算法
1.1 四种坐标系的定义
为了便于阐述和分析,建立追踪器坐标系O(X,Y,Z)、摄像机坐标系Oc(Xc,Yc,Zc)、像墙面坐标系Oo(u,v)和目标航天器坐标系o(x,y,z),分别定义如下:
(1)图像坐标系Oo(u,v):是以像素为单位表示的图像坐标系,原点Oo位于图像的一个顶点,(u,v)表示每一像素在图像中的列数和行数,图像中心点O1的图像坐标为(uo,vo);
(2)摄像机坐标系Oc(Xc,Yc,Zc):原点Oc定义为摄像机光心,Xc轴和Yc轴分别与图像的u轴和v轴平行,Zc轴为摄像机的光轴,它与图像平面垂直。光轴与图像平面的交点,即为图像平面的中心点 O1。|OcO1|即为摄像机焦距 f。
(3)追踪器坐标系O(X,Y,Z):该坐标系定义在追踪器上,其原点定义在追踪器质心,其X轴、Y轴、Z轴可根据追踪器的形状来规定,摄像机坐标系Oc与追踪器坐标系固联。
(4)目标器坐标系o(x,y,z):该坐标系定义在目标特征光点上,其x,y,z轴可根据具体特征光点的设置而定,本文中参见图1.四个特征点A、B、C、D构成正方形,故将原点o定义为正方形中心,x轴系。各坐标系见图1。

图1 各坐标系的定义及特征点的设置Fig.1 Definition of the four coordinate systems and configura-tion of reference points
1.2 三目视觉测量原理
利用 C1,C2,C3三台摄像机成像平面上投影点。若没有任何误差存在,图示三条直线 Oc1P1,Oc2P2,Oc3P3应交于空间同一点(即P点)。但实际上,由于摄像机标定误差,特征像点的定位匹配误差等,使得这三条直线交于空间三点,即P1,P2和P3,它们分别为直线Oc1P1,Oc2P2和Oc3P3的两两交点,其坐标值可以由双目视觉的特征点定位算法给出。
三目视觉测量原理见图2。
假设P点在追踪器下坐标为P(X,Y,Z),则其估计值应满足目标函数
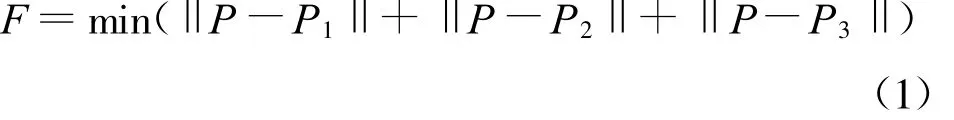
由上式确定的P点坐标即可认为是P点真实坐标的最优估计。具体过程如下:
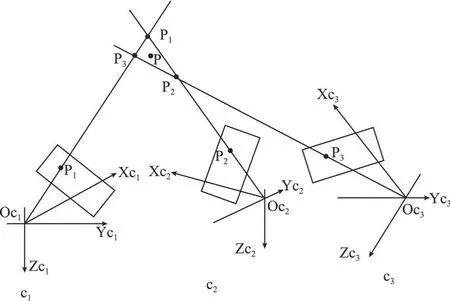
图2 三目视觉定位原理Fig.2 Trinocular vision positioning

式(2)(3)(4)中 (ui,vi,1,i=1,2,3分别为点 P′1,P′2和 P′3在各自图像坐标系中的齐次坐标,(X,Y,Z,1)为点P在追踪器坐标系下的齐次坐标。设点P1,P2,P3在追踪器坐标系下的坐标分别为Pi(Xi,Yi,Zi),i=1,2,3。由双目视觉定位算法[7]可以得到该坐标的最小二乘结果为:


式(5)中P点在追踪系坐标系中的坐标为(X,Y,Z),则其估计值应满足目标函数

要满足式(6)只需同时满足下列条件:
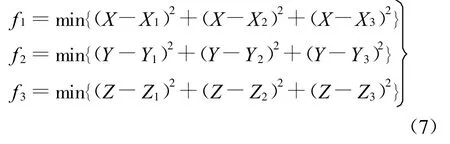
由各变量与算术平均数的离差平方和最小,可知最优的X,Y,Z值为

上式即为P点在追踪器坐标系下的坐标值P(X,Y,Z)的最优估计。
与单目视觉算法相比较,利用三目视觉定位,每个特征点都可以得到其唯一确定的位置坐标,由于求解的都是线性方程,存在解析解,故无需迭代求解。与双目视觉测量算法相比,三目视觉算法也有明显的优势。一方面,通过方差处理,提高了特征点的定位精度。另一方面,有研究表明,利用三目视觉的方法从图像中提取特征点并通过图像匹配来获得这些特征点的空间坐标的方法,可以大大减少匹配的时间以及误匹配的可能性[8]。除此之外,三目测量亦是一种冗余度技术的应用,三台摄像机互为备份,当有一台出现故障后,另两台可利用双目算法继续完成测量任务,增加了测量系统安全可靠性,这在航天技术应用中也是至关重要的。综上所述,三目视觉测量方法要优于单、双目测量。
1.3 相对位置和相对姿态的计算
通过上述方法求得各特征点在追踪器坐标系中的位置坐标后,我们就可以通过坐标转换进一步求得追踪航天器和目标航天器之间的相对位置和相对姿态。
如图1所示,目标航天器上设置的4个特征光点A,B,C,D位于同一平面中并构成正方形,可得目标中心位置Op(Xop,Yop,Zop)为[7]

目标的姿态以欧拉角 φx,φy,φz表示,它们分别表示目标器坐标系与追踪器坐标系三个轴之间的相对旋转角[7],即

式(10)中L=|AB|为正方形的边长。
2 基于三目光学测量的建模与误差分析
2.1 运动参数简化模型
为了更清楚地了解上述过程的物理意义,同时便于误差分析和简化计算,下面我们讨论在一种简单的摄像机配置下的空间点重建,如图3所示。
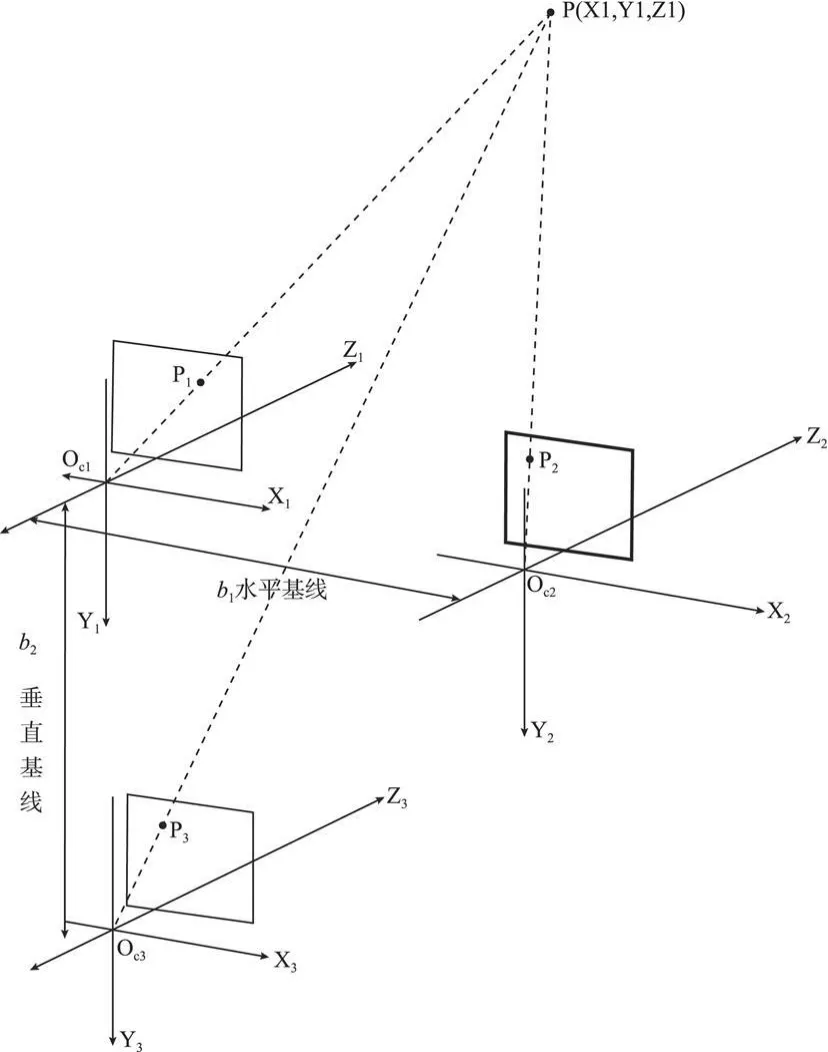
图3 三摄像机的简单配置Fig.3 A simple configuration of the three cameras
有3台CCD摄像机C1,C2和C3,对空间点P同时进行观测,并假设:
(1)焦距f相等,内外参数已标定且均相等。
(2)三摄像机光轴互相平行,C1,C2的X轴互相重合,C2,C3的Y轴互相重合。
(3)摄像机C1和C2间距为b1(称为水平基线horizontal baseline长度),C2和C3之间间距为b2(称为垂直基线vertical baseline长度),即C1沿X轴右移距离b1后与C2重合,C2沿Y轴下移距离b2后与C3重合。
(4)P1,P2,P3三个像点已精确匹配,对应空间同一点P。
所以,若特征点P点在摄像机C1坐标系中的坐标值为(X1,Y1,Z1),则其在C2坐标系的坐标值即为(X 1-b1,Y1,Z 1),在 C3坐标系的坐标值即为(X1,Y1-b2,Z1)。
说明:由于摄像机是固定在追踪器上,摄像机坐标系和追踪器坐标系之间的相对位置和姿态在运动过程中是保持不变的,所以为了方便,我们仅需考虑目标器坐标系与摄像机坐标系之间的相对位置及姿态的测量。
在上述约束条件下,由针孔模型[6]的比例关系可得:

式(11)至(16)中,uo,vo,αx,αy为摄像机内部参数,uo,vo为图像中心点在像平面坐标系中的坐标,αx=f/d x,αy=f/d y,这里 f是摄像机焦距,d x,d y为每一个像素在u轴和v轴方向上的实际物理尺寸。(u1,v1),(u2,v2)和(u3,v 3)分别为点 P1,P2,P3的图像坐标。
下面由方程(11)~(16)来求解(X1,Y1,Z1)。显然,理论上有:u1=u3,v 1=v2由方程(11)/(13)得
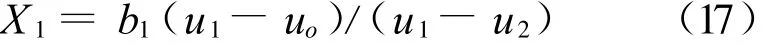
同理有
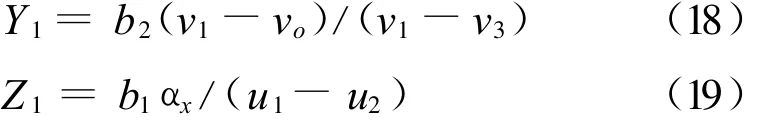
或表示为
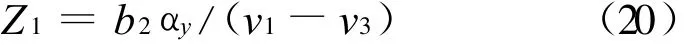
式(17)至(20)中,u1-u2称为水平视差(horizontal disparity),v1-v3称为垂直视差(vertical disparity),视差是由于摄像机位置不同使同一点P在图像中的投影点不同引起的。由式(19)或(20)可知,P点距离越远(即Z1越大),视差越小。当 P点趋于无穷远时,Oc1P1,Oc2P2与Oc3P3趋于平行,视差趋于0。
2.2 针对简化模型的误差分析
针对式(17)至(20)建立的测量模型,对其进行误差分析。首先分析X方向,由于

所以:
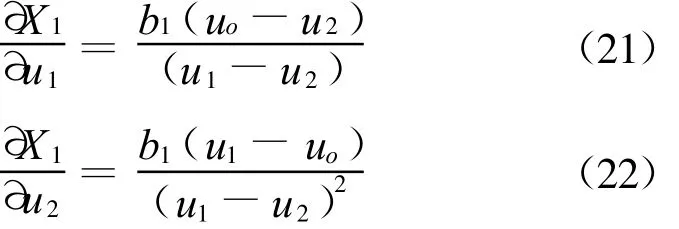
所以有:
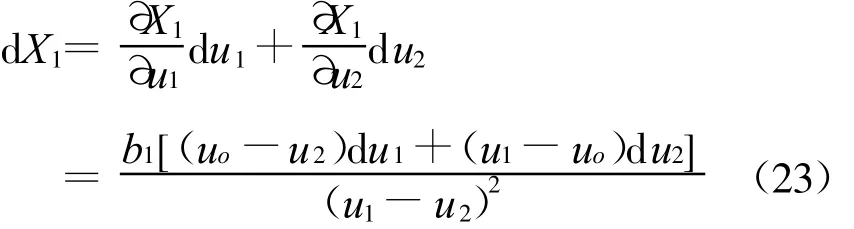
同理分析Y方向,由于
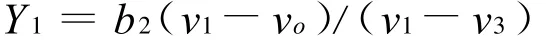
所以:

同理分析Z方向,由于
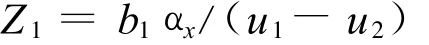
所以:
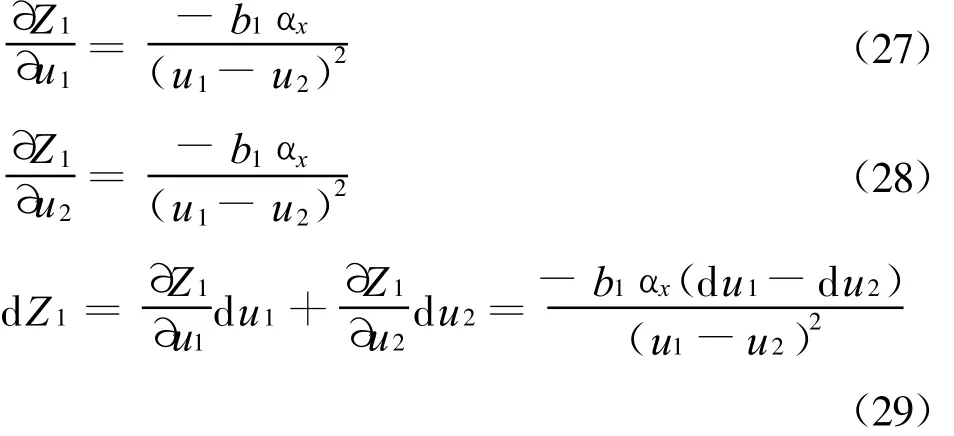
式(21)至(29)中,d u1,d u2,d u3,d v1,d v2,d v3分别为特征点在三个摄像机相平面上的像点的匹配误差,由于d u1,d u2,d u3,d v1,d v2,d v3是统计独立的,可设d u1=d u2=d u3=d v1=d v2=d v3,即D(u1)=D(u2)=D(u3)=D(v1)=D(v2)=D(v3)=D(u),对上面各式两边分别取方差,则X方向的定位误差为:

Y方向的定位误差为:

Z方向的定位误差为:
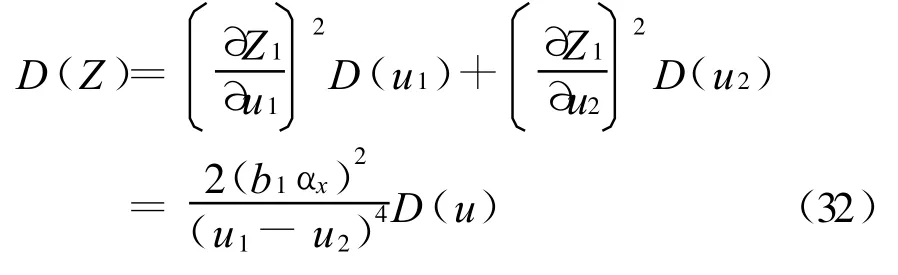
由此对式(9)两边取方差得到两航天器间相对位置的误差[5]为:
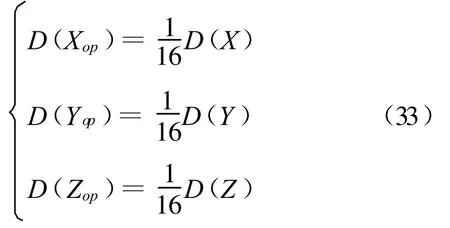
同理对式(10)取方差得到两航天器间相对姿态的误差[5]为:
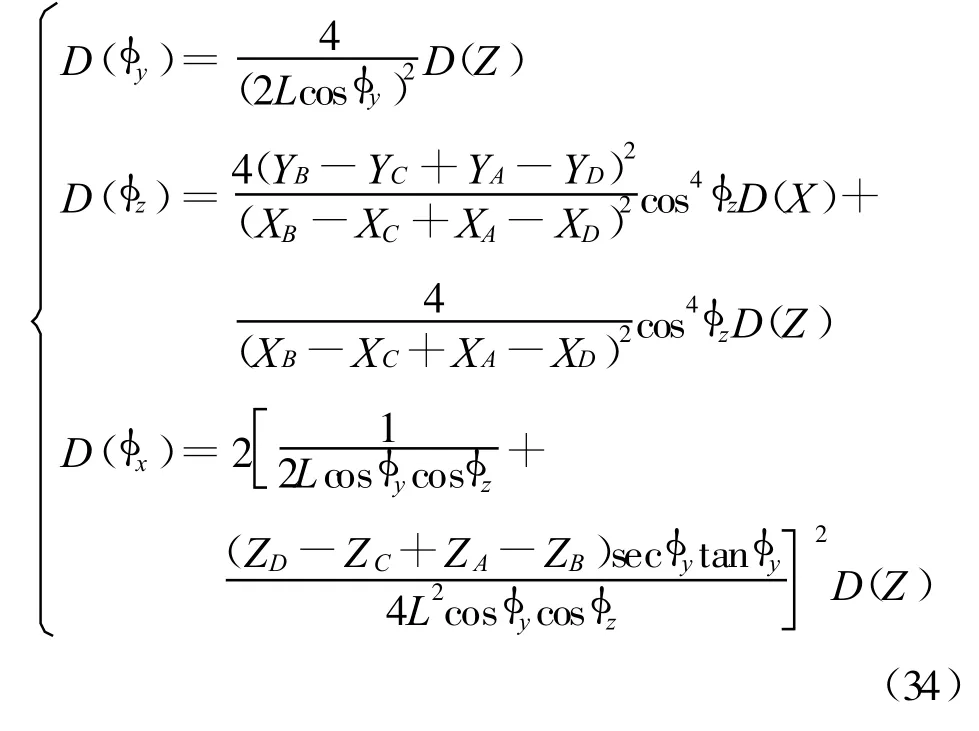
3 仿真结果及比较分析
为验证本文所提出的三目视觉测量算法的有效性,利用Matlab进行数值仿真。仿真条件如下:
摄像机焦距f=1,即采用归一化的图像坐标;
图像分辨率4000*3000;
每像素物理尺寸:12μm×12μm;
特征点匹配误差:0~5像素;
三台摄像机相对位置:b1=0.4 m,b2=1 m;
四个特征点构成的正方形边长:L=2m假设某特征点在追踪系中精确位置为X=-1,Y=1,Z=100,匹配误差在0~5像素之间变化,分别利用双目和三目视觉算法确定该点在追踪系下的坐标值,分别得其X,Y,Z三个方向定位的误差结果见图4。
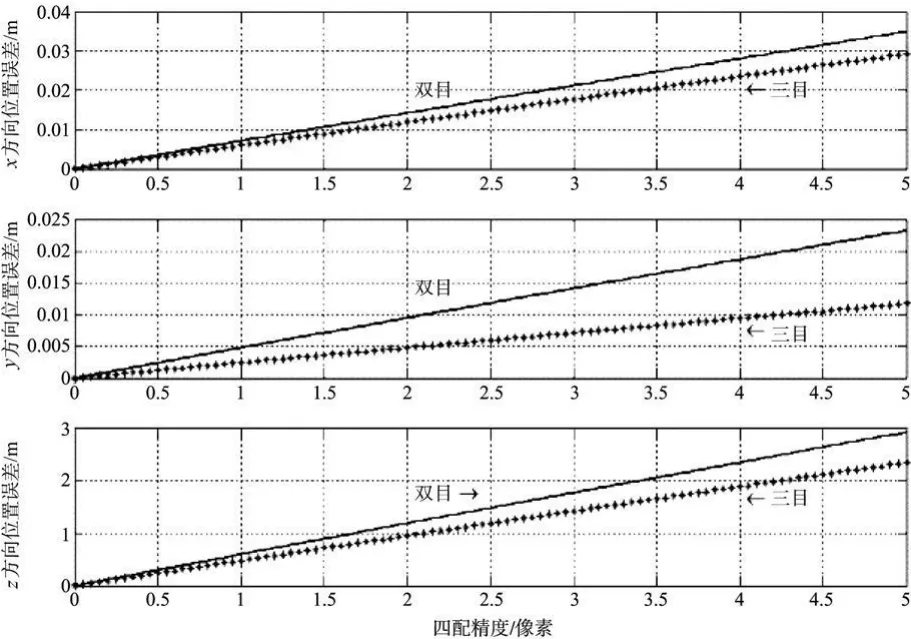
图4 空间点定位误差与匹配精度的关系曲线Fig.4 Relation curve between positioning deviation of a reference point and its matching error
由图4我们可以看到,在特征像点匹配误差相同的情况下,通过三台摄像机观测得到的每个特征点的定位误差均比双目视觉算法的误差小。并且通过计算得知,在该位置上X,Y,Z方向的误差分别减小了16.37%,66.47%,19.76%。经大量数据仿真发现,对于空间其他位置上的特征点的定位也有相同结论,故不再列出类似图形曲线。所以,我们可以得出结论:与双目视觉测量方法相比,三目视觉测量可以有效减小特征点的定位误差,尤其是在Y方向上定位精度显著提高。这一结论具有一般普遍性,可以从以下两方面加以解释。直观上,通过比较三目(即图3)与双目摄像机配置图[7]可以发现,三目配置实际是在双目的基础上在Y方向上增加一台摄像机;理论上,通过比较式(17)至(19)与双目视觉的定位方程[5]可见,Y方向的定位算法有了较大改进,而X,Z方向的仍然相似。即在X、Z方向的定位上,算法没有变化,仅仅是由于增加了一个冗余CCD后求平均使得精度有所提高。而对于Y方向,算法有了改进。双目视觉的定位方程中,u1,u2,v 1三个测量量都会引入误差,而三目视觉中Y的误差来源仅有v1和v3两项。由于在2.2节中已假定每个测量量引入的误差相同,所以三目视觉算法在Y方向上的定位精度提高幅度大于X和Z方向。
4 结 论
本文主要针对航天器交会对接过程中目标航天器与追踪航天器间的相对位置和姿态的测量问题,采用CCD摄像机作为传感器的光学方法,获得了较好的结果。文章在总结了单双目测量方法优缺点的基础之上,提出了三目视觉的测量方法,阐述了其基本原理,建立了数学模型,并对测量系统中的误差进行了分析。文章最后通过Matlab仿真,对三目视觉的定位误差与双目视觉做了定量的比较。仿真结果表明三目视觉的测量方法有效。与单目视觉测量相比,三目视觉算法无需迭代求解非线性方程,因而具有很好的实时性和更高的测量精度;而与双目视觉相比,三目视觉能很好地克服图像匹配带来的误差,提高特征点的定位精度,因此能为航天器的相对位姿参数提供更为精准地数据。除此之外,三目测量亦是一项冗余度技术,使得测量系统更具安全可靠性。因此,该方法对航天器在轨实时应用具有重要参考价值。
[1] 吴宏鑫,胡海霞,解永春,等.自主交会对接若干问题[J].宇航学报,2003,24(2):132-137.[WU Hong-xin,HU Hai-xia,XIE Yong-chun,et al.Several questions on autonomousrendezvous docking[J].Journal of Astronautics,2003,24(2):132-137.]
[2] 曹喜滨,张世杰.航天器交会对接位姿视觉测量迭代算法[J].哈尔滨工业大学学报,2005,37(8):691-694.[CAO Xi-bin,ZHANGShi-jie.An iterative method for vision-based relative pose parametersof RVD spacecrafts[J].Journal of Harbin In Institute of Technology,2005,37(8):691-694.]
[3] HOCJ,MCDLAMROCHNH.Automatic spacecraft docking using computer vision-based guidance and control techniques[J].Journal of Guidance,Control,and Dynamics,1993,16(2):281-288.
[4] PHILIPNK,ANANTHASAYANAMMR.Relative position and attitude estimation and control schemes for the final phase of an autonomous docking mission of spacecraft[J].Acta Astronautica,2003,52:511-522.
[5] 张庆君,胡修林,叶斌,等.基于双目视觉测量的航天器相对位置和姿态的测量方法[J].宇航学报,2008,29(1):751,851,951,61.[ZHANG Qing-jun,HU Xiu-lin,YE Bin,et al.Binocular vision-based relative position and attitude determination between spacecrafts[J].Journal of Astronautics,2008,29(1):751,851,951,61.]
[6] 马颂德,张正友.计算机视觉—计算理论与算法基础[M].北京:科学出版社,1997:57.[MA Song-de,ZHANG Zheng-you.Computer vision computation theory and algorithm principle[M].Beijing:Science Press,1997:57.]
[7] 张淑琴.空间交会对接测量技术及工程应用[M].北京:中国宇航出版社,2005,10:342-343.[ZHANG Shu-qin.Measurement technology of space rendezvous and docking and engineering applications[M].Beijing:China Astronautic Publishing House,2005,10:342-343.]
[8] 何炳蔚,林志航,杨明顺,等.逆向工程中基于三目视觉自动提取并构造复杂曲面边界技术[J].机器人,2002,24(1):66-70.[HE Bing-wei,LIN Zhi-hang,YANG Ming-shun,et al.In reverse engineering the method for extracting and modeling boundary of complex surface based on trinocular stereo vision[J].Robot,2002,24(1):66-70.]

