机动目标拦截的变结构制导律设计与实现

马克茂,马 杰

(哈尔滨工业大学航天学院,哈尔滨 150080)

0 引 言

在导弹的末制导过程中,尤其是在制导的末端,影响制导精度的两个主要因素是目标的逃逸机动和弹体动态响应过程[1]。目标机动的影响可以在制导律中加以补偿,以提高制导精度,如增广比例导引制导律[2],但在制导律的实现过程中存在目标机动信息的估计问题。弹体动态响应过程的时间常数决定了弹体对制导律给出的过载指令的响应快慢,大的弹体时间常数导致导弹过载跟踪制导指令的滞后,在制导末端会严重影响制导性能[3]。针对弹体的动态特性,目前研究中主要从两方面考虑来提高制导精度。一方面,可以采用直接侧向力等快响应技术[4],来提高弹体的动态响应速度,但采用直接侧向力在导弹控制回路中引入了离散特性及很大的气动干扰效应,给自动驾驶仪和制导探测系统的设计带来困难[5];另一方面,可以在制导律设计过程中直接考虑弹体的动态特性对制导回路的影响[6],并采用一定的制导律设计方法消除这种影响,从而提高制导精度。

本文针对机动目标的平面拦截问题,应用变结构控制方法与扩张观测器技术研究了制导律设计与实现问题。针对上面讨论的影响制导精度的两个主要因素,在设计过程中,应用增广比例导引的思想设计变结构制导律的切换函数,因而可有效地应对目标的机动;同时在弹体过载跟踪回路的输入端应用变结构控制,使制导系统的状态变量在有限时间内到达滑动平面,因而消除了弹体时间常数对制导精度的影响。在设计切换函数时所采用的增广比例导引需要利用目标的机动加速度信息,同吮,在所设计的变结构制导律中还需要用到目标机动加速度的变化率信息,而一般导引头只能提供视线角度信息,雷达导引头还可以提供有关的相对距离信息,但无法提供目标机动信息,导致制导律实现困难。本文假设弹目相对距离及其变化率信息、视线转角可测量得到,采用高增益观测器对制导律中所需要的视线转率信息进行快速估计,并提出了对高增益观测器进行二次扩张、利用扩张观测器变量分别对目标的机动加速度及其变化率进行快速估计的方法,实现了所设计的变结构制导律。最后,对所设计的制导律及制导信息估计方法进行了仿真验证,并对仿真结果进行了分析,说明了方法的有效性。

1 数学模型与问题描述

为便于推导以说明设计思想,本文考虑拦截平面内的弹目相对运动,如图1所示,将导弹与目标均视为质点,分别用M和T表示,他们的连线LOS为视线,q为视线角,r为弹目相对距离,别为导弹和目标的速度矢量。

图1 弹目相对运动关系Fig.1 Relative motion geometry of missile and target

图1 中给出的弹目相对运动关系可描述为

其中amr、atr分别为导弹和目标在视线方向上的加速度分量,amq、atq分别为导弹和目标在垂直于视线方向上的加速度分量。考虑到物理上受到的能量和响应速度的限制,导弹实际所能提供的最大过载是有限的,同样目标的机动过载也是有限的,因此存在常数AM＞0,AT＞0使得

记末制导开始时刻为0,不失一般性,假设目标机动满足如下条件。

假设1:存在常数A1＞0,A2＞0,使得

为便于设计,将弹体动态与自动驾驶仪所构成的过载跟踪回路用简化的一阶惯性环节来近似描述,其动态方程为

其中TB为时间常数,amc为制导律环节提供给自动驾驶仪的过载指令,Δf(t)为不确定性,代表过载回路的建模误差和所受到的外部干扰,假设其满足如下条件:

假设2:不确定性 Δf(t)是有界的,即存在常数Bf≥0,使得|Δf(t)|≤Bf,∀t≥0。

本文所研究的问题为:针对由式(1)-(4)所描述的制导控制系统,在不确定性存在的条件下设计制导律,同时假设弹目相对距离及其变化率、视线角、导弹横向过载可测量得到,对所设计的制导律进行实现。

2 变结构制导律设计

在末制导过程中导弹沿视线方向的加速度分量一般是不可控的。当弹目接近速度小于零、视线转率接近于零时,根据平行接近原理,导弹与目标在视线方向上的加速度分量对于导弹拦截目标没有影响[7],因此在制导律设计时可以不考虑导弹与目标在视线方向的加速度分量,即将式(1)改写为

为了应对目标的逃逸机动,按照增广比例导引的思想,在比例导引中增加目标机动加速度的补偿项,设计变结构制导律的切换函数为

其中常数N为导航比,满足N＞2。先不考虑过载跟踪回路中不确定性 Δf(t)的影响,令˙s=0,求解加速度指令,可得

这里的ace即为变结构控制中的等效控制。

基于上述等效控制,设计制导律如下

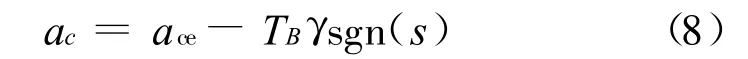
其中 γ＞Bf。ac为变结构制导律,由等效控制和切换控制组成。针对这一制导律有如下结论。

命题:制导律(7)、(8)可使制导系统(2)、(4)的状态在有限时间内达到切换面{s=0}并保持在切换面上,进入滑动模态运动。

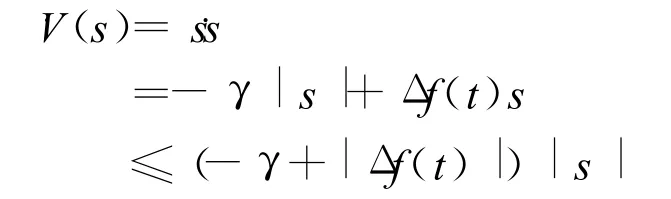
考虑假设2,可得

其中 λ=γ-Bf。由γ取值范围可知λ＞0。因此由(9)式可知,当s(t)≠0时,在变结构制导律(7)、(8)作用下系统状态向切换面趋近,而系统状态如果在切换面上,则(9)式可保证系统状态维持在切换面上,进行滑动模态运动。设s(0)≠0,对(9)式进行积分

令V(s(T))=0,则由上式可得

即制导系统的状态将在有限时间内到达切换平面{s=0}上。由(9)式可得 s˙s≤-λ|s|,这一条件保证了当系统状态到达切换平面后将保持在切换面上,即进入滑动模态运动。命题证毕。

在切换平面上,系统状态满足s=0,由(6)式可知,此时下述条件成立

将其代入(2)式,可得滑动模态方程如下:

即标准的目标无机动、弹体动态时间常数为零条件下的比例导引方程,由N ＞2、˙r＜0可得滑动模态的稳定性。由方程(12)、(13)可以看出,制导系统的状态进入滑动模态运动后,滑动模态不受目标机动特性、过载跟踪回路的动态特性等因素的影响,根据比例导引的最优性讨论[1,7],可知变结构制导律可以有效地克服目标机动和过载跟踪回路动态特性对制导精度的影响。

(4)式给出的是过载跟踪回路的一个简化模型,同实际系统相比,存在着不确定性。过载跟踪回路中的不确定性及外部干扰是由变结构制导律(8)式中的增益γ进行抑制的。由(10)式可以看出这一增益还影响着系统状态到达切换面的时间,增益越大,则系统状态达到切换面的时间越短,但引起的振颤也会变大,因此在设计中需要对不确定性的抑制作用、系统状态达到切换面的时间和振颤等因素进行综合考虑。

3 制导律的实现

假设弹目相对距离信息、视线角、导弹横向过载等可测量得到(由导弹的导引头、加速度计等给出),在方程(2)、(4)、(5)中,将与相对距离有关的信息视为已知时变参数,令

则(2)式可描述为

其中

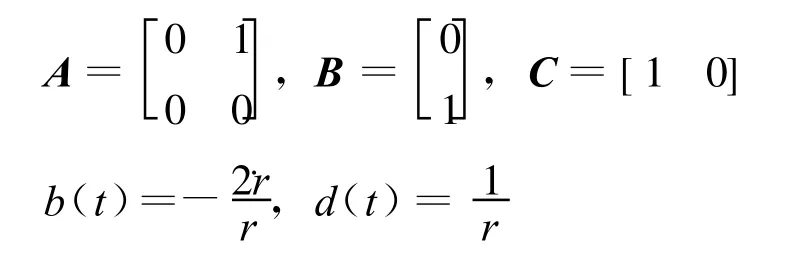
将时变项b(t)x2与系统的输入写在一起,则矩阵A为定常矩阵,系统(14)、(15)具有积分器的形式,建立高增益观测器可以方便地对˙q进行快速估计。从变结构制导律(7)、(8)式可以看出,在制导律实现时还需要目标机动加速度及其变化率a tq、˙a tq的信息。针对这些制导信息,这里在高增益观测器[8-9]的基础上,对观测器的变量进行二次扩展,分别用于对制导信息中atq和˙atq的快速估计。为此,针对系统(14)、(15),建立如下高增益观测器

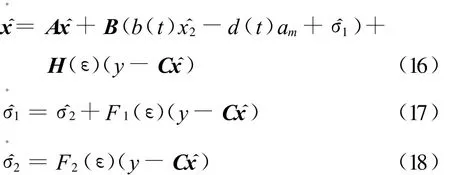
其中^x=[^x1^x2]T为观测器状态变量,用来估计视线转率,^σ1、^σ2为扩展观测器变量,用来估计目标机动加速度及其变化率。观测器增益为

参数 αi均为实数(i=1,2,3,4),使得

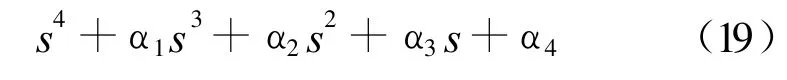
为Hurwitz多项式,ε＞0为小的设计参数。

下面分析观测器的收敛性。为此,定义观测误差向量为

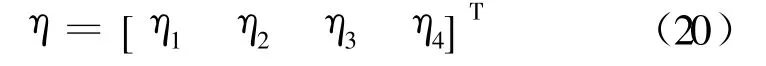
其中

则可得观测误差的动态方程如下

其中

针对误差系统(21),定义 W(η)=εηTPη,其中P＞0为如下Lyapunov方程的解

由于要求(19)式为Hurwitz的,因此针对任意给定的正定矩阵 Q,方程(22)存在唯一正定解 P。计算W(η)沿误差系统(21)对时间的导数,可得

将(21)式代入,可得

将方程(22)代入,可得

其中 λmin(Q)为矩阵 Q的最小特征值。在末制导过程中导引头存在最小作用距离r0,当r＜r0时,制导回路断开,制导过程结束,因此在制导过程满足弹目相对距离r≥r0,且制导过程会在有限时间内结束,设该时间为Tg。由上面讨论可知,对于 ∀t∈[0,Tg),b(t)、d(t)及其导数都是有界的,因此(21)式中的h(t)也是有界的。记

则由(23)式可得

显然存在ε*＞0,使得对于任意ε∈(0,ε*),如下条件均成立:

令

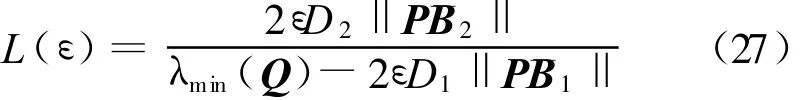
则由(25)式可知,当‖η‖＞L(ε)时有˙W(η)＜0成立,因此可得观测误差的实用收敛性,观测器最终的估计精度由(27)式给出。从(27)式可以看出估计精度随着ε的减小而提高。从观测误差的动态方程(21)式可以看出,ε的减小同样会提高观测器的收敛速度。

根据(20)式关于跟踪误差的定义,当ε足够小时忽略观测误差的影响,可以得到目标机动加速度及其变化率的估计式如下

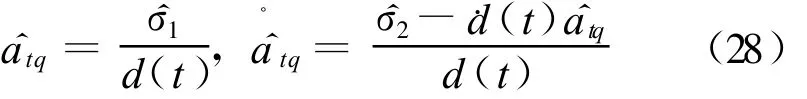
第2节所设计的变结构制导律的实现包括由(16)-(18)式给出的扩展高增益观测器、(28)式和如下各式

在高增益观测器中,随着ε的减小,观测器的增益变大,在观测误差中会产生短时间的尖峰现象[8,10],而这种尖锋现象会通过(29)-(31)式向制导回路传递,对制导回路的稳定性和性能产生影响。但是考虑到导弹过载的实际限制条件(由式(3)给出),在这个传递通道上实际上存在着饱和非线性环节,而饱和非线性环节正是抑制这种尖峰现象在系统中传递的常用手段,因此这里引入的高增益观测器不会对制导系统的稳定性和性能产生影响。为避免过大的制导指令直接传给过载跟踪系统,在制导律实现时可以在(29)式给出的制导指令后串联幅值为AM的饱和环节。

4 仿真验证

考虑拦截平面内的末制导过程,假设导弹可提供的最大横向加速度为aM=400 m/s2,导引头中断寻的制导的距离为r0=100 m。过载跟踪回路中弹体动态的时间常数取为TB=0.3 s。高增益观测器的设计参数设置如下

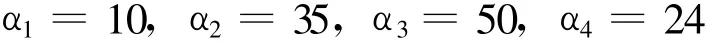
上述参数对应于(21)式中¯A的特征值为

参数ε选择为ε=0.01。变结构制导律中参数γ选择为 γ=15。

仿真中观测器状态的初值均置为0,目标机动加速度取为

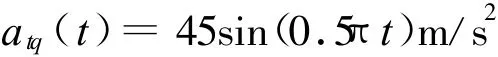
弹目相对运动的初值设置为

基于上述给定的参数对末制导过程进行了仿真,图2-图6分别给出了视线角、视线转率、目标机动加速度及其变化率、制导律给出的指令加速度和导弹的实际加速度的仿真结果。经仿真计算得到的脱靶量为0.06 m。

图2 视线角的估计Fig.2 Estimation of line-of-sight angle

从图2-图5给出的观测器估计的仿真结果中可以看出,除了在开始阶段存在短时间的尖峰现象外,所设计的观测器对于视线角、视线转率、目标机动加速度均具有很好的估计效果,而对目标机动加

图3 视线转率的估计Fig.3 Estimation of ling-of-sight rate

图4 目标机动加速度的估计Fig.4 Estimation of target's maneuvering acceleration

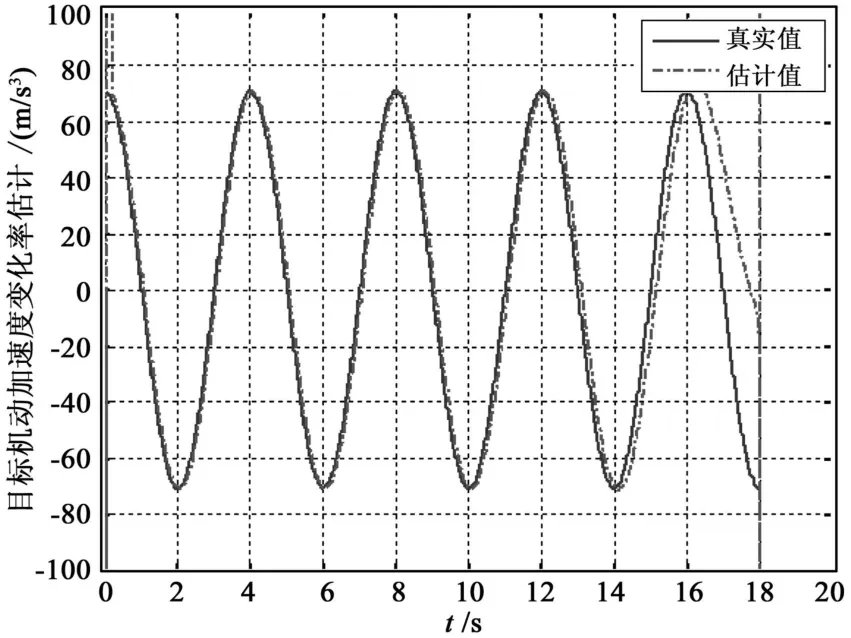
图5 目标机动加速度变化率的估计Fig.5 Estimation of the rate of target's maneuvering acceleration

速度的变化率的估计在制导末端误差稍大,这一点从(20)式中给出的观测误差定义中也可以看出来,前三个变量的估计由于小参数ε的作用使得误差很小,第四个变量的估计与观测误差是同数量级的,因此导致误差稍大,但是对制导精度影响并不大,这点从最终的脱靶量仿真结果可以看出。

图6 指令加速度与实际加速度Fig.6 Command acceleration and real acceleration

从图6给出的仿真曲线可以看出,大约在末制导开始后4秒左右制导律给出的加速度指令开始频繁地切换,表明系统状态开始进入了滑动模态运动。仿真给出的指令加速度过载在制导开始阶段存在短时间的饱和现象,体现了在指令过载通道中串联的饱和环节对观测器尖峰现象的抑制作用。另外,图中还可以看出导弹实际横向加速度滞后于指令加速度,这一滞后反映了(4)式描述的过载跟踪回路的动态,从图中可以看出这一滞后与仿真中所选取的弹体时间常数是一致的。

由于在r≤r0时制导系统给出的指令为0,导弹终止制导而进行惯性飞行,因此目标进行正弦机动的初始相位对脱靶量是有影响的。针对上述参数,改变目标机动的初始相位,选择目标机动加速度为

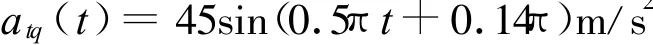
仿真所得到的曲线与前面的仿真结果类似,得到的脱靶量为0.19 m,说明了目标机动的初始相位对脱靶量的影响。

5 结 论

针对影响制导性能的两个主要因素,即目标机动和弹体的动态特性,对制导律的设计与实现问题进行了研究。采用变结构控制方法设计了制导律,在切换函数的设计中对目标机动加速度进行了补偿,在切换控制中考虑了弹体动态特性的影响。应用高增益观测器方法对制导信息进行快速估计,提出了对目标机动加速度的变化率进行估计的方法。对所提出的制导律设计和实现进行了仿真研究,仿真结果说明了方法的有效性。

为便于给出制导律及其实现的表达式以说明采用的设计思想,本文考虑了平面内弹目相对运动的制导问题。对比本文考虑的平面制导问题的数学模型和三维空间制导系统的数学模型[11],可以看出本文给出的制导律设计与实现方法可以直接推广到三维空间拦截问题的制导律设计。

[1] Zarchan P.Tactical and strategic missile guidance[M].AIAA Inc,Reston,VA,USA,3rd Ed,1997.

[2] 张宏,夏群力,祁载康,等.基于目标机动补偿的增强型比例导引性能分析[J].红外与激光工程,2007,36(Sup):82-87.[ZHANG Hong,XIA Qun-li,QI Zai-kang,et al.Augmented proportional navigation with maneuvering target compensation[J].Infrared and Engineering,2007,36(Supp):82-87.]

[3] 魏先利,夏群力,祁载康.姿态及过载自动驾驶仪比例导引对比研究[J].弹箭与制导学报,2003,23(4):5-8,12.[WEI Xian-li,XIA Qun-li,QIZai-kang.Comparing study of proportional navigation guidance law of attitude and acceleration autopilots[J].Journal of Projectiles,Rockets,Missiles and Guidance,2003,23(4):5-8,12.]

[4] Innocenti M,Thrkral A.Simultaneous reaction jet and aerodynamic control of missile systems[C].AIAA Aircraft Design,Systems and Operations Meeting Monterey,CA,USA,Aug.11-13,1993:347-354.

[5] Jeffrey L P,Christopher J R,Steven J.A comparison of turbulence models for a supersonic jet in transonic crossflow[C].Proceedings of the 39th AIAA Aerospace Sciences Meeting and Exhibit.Reno,NV,USA,Jan,8-11,2001:1-22.

[6] 侯明善.大弹体动态滞后末端区制导系统优化设计[J].宇航学报,2008,29(1):145-149.[HOU Ming-shan.Optimal guidance in end-game regions for a missile with large lag[J].Journal of Astronautics,2008,29(1):145-149.]

[7] 娄寿春.导弹制导技术[M].北京:宇航技术出版社,1989.[LOU Shou-chun.Missileguidance technology[M].Beijing:Aerospace Technology Press,1989.]

[8] Khalil H K.High-gain observers in nonlinear feedback control,in new directions in nonlinear observer design[M].Springer Berlin/Heidelberg,Germany,1999:249-268.

[9] Freidovich L B,Khalil H K.Performance recovery of feedback-linearization-based designs[J].IEEE Trans.Automat.Control,2008,53(10):2324-2334.

[10] Atassi A N,Khalil H K.A separation principlefor thestabilization of a class of nonlinear systems[J].IEEE Trans.Automat.Control,1999,44(9):1672-1687.

[11] 佘文学,周凤岐.三维非线性变结构寻的制导律[J].宇航学报,2004,25(6):681-685.[SHE Wen-xue,ZHOUFeng-qi.High precision 3-D nonlinear variable structureguidance law for homingmissile[J].Journal of Astronautics,2004,25(6):281-285.]