基于形状的行星际小推力转移轨道初始设计方法

尚海滨,崔平远,乔 栋

(北京理工大学深空探测技术研究所,北京100081)

0 引 言

在星际探测任务中,采用小推力发动机可有效提高探测器的有效载荷,增加探测任务科学回报[1]。星际小推力转移轨道的设计通常分为初始设计和精确设计两步,初始设计的目的是为精确设计提供可行的设计初值[2]。与脉冲转移轨道不同,小推力转移弧段不能用传统的圆锥曲线来刻画,许多脉冲轨道设计中的理论与方法不再适用,这给行星际小推力转移轨道的设计带来了困难,寻求一种快速有效的初始设计方法成为目前研究的热点[3]。

基于形状的星际小推力轨道设计理论是目前较为有效的一类方法。基于形状逼近思想,Petropoulos提出了一种基于正弦指数曲线逼近的设计方法[4-5],由于正弦指数曲线不能满足始末端速度边界条件,该方法只能用于设计发射及射入能量不为零的轨道。针对此,Wall又提出了一种基于六次逆多项式曲线逼近的设计方法[6],该函数曲线是通过对最优转移轨道数据拟合得到的,由于具有七个待定参数,能够同时满足始末端位置速度边界条件以及飞行时间约束,因此可对任务类型转移轨道进行设计。然而,由于没有考虑转移轨道的实际动力学约束要求,导致该方法经常出现遗漏可行轨道的情况。

本文针对以上问题,对逆多项式逼近轨道的动力学可行性进行了深入分析,推导了关键系数的可行范围;然后,基于改进的逆多项式逼近理论,建立了一种简单有效的行星际小推力转移轨道初始设计模型,同时,为了获得全局最优转移机会,采用了微分进化算法对搜索参数进行寻优计算。最后,以地球-火星和地球-金星小推力转移为例,对所提算法进行了仿真验证。

1 逆多项式逼近策略

在日心引力场中,采用极坐标系描述的探测器运动方程为:

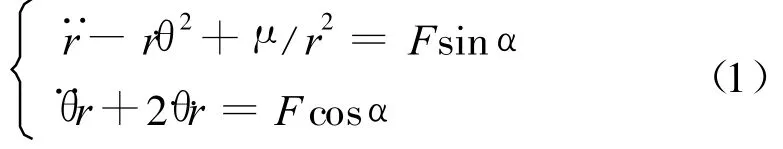
其中:r为探测器轨道的矢径大小,θ为在日心惯性系中的相角,μ为太阳的引力常数,F为推力加速度大小,α为推力方向角。

由于推力加速度项的存在,方程(1)不存在闭环解析解。为便于求解,Petropoulos和Wall先后提出两种函数来描述探测器的运动轨迹:

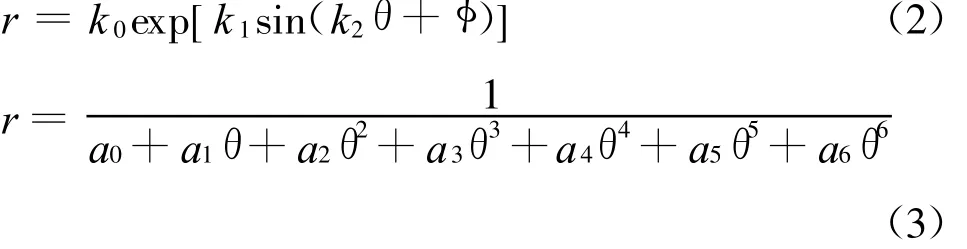
理论推导表明,方程(3)提出的逆多项式曲线可以用于包括交会轨道在内的任务类型的轨道转移问题,相比方程(2)具有更广的应用范围。另外,由于方程(3)是基于最优转移轨道数据拟合得到的函数,因此具有更优的轨道转移特性。Bradley基于方程(3),通过使探测器轨道分别满足始末端的位置速度边界条件,得到了解析的逆多项式曲线的参数a0～a2及a4～ a6。

进一步,假定转移过程中推力矢量始终沿飞行路径角方向或其反方向,即令 α=γ+mπ(m为0或1),可以得到相角 θ变化率为:

由文献[6]可知,在给定始末端边界条件的情况下,要获得解析的转移轨道,只存在a3一个未知量,该参数可根据时间约束条件通过迭代求解。然而,文献[6]所给方法在迭代过程中经常会出现˙θ在某一相角范围内有˙θ＜0,导致所求得的转移时间t出现虚值,无法得到满足条件的a3,从而可能丢失可行的转移轨道。

2 动力学可行性分析

对于可行的转移轨道,˙θ在转移过程中的变化趋势应该保持不变。如果始终有˙θ≥0,则对应顺行轨道;如果始终有˙θ＜0,则对应逆行轨道。本文针对顺行轨道展开讨论,根据式(4),由于 μr4＞0,若要使˙θ≥0,必须满足如下条件:

为便于描述,假设探测器初始相角 θ1=0,末端相角为0≤θ2≤2π,则探测器转过的相角为 θf=2nrevπ+θ2(nrev为探测器在转移过程中绕太阳转过的完整圈数)。分别令

则 a′4、a′5和 a′6分别可以表示为 :

其中:辅助变量 w′1、w′2和 w′3可以表示为

其中:r2为探测器轨道末端矢径大小,γ2为轨道末端飞行路径角。

根据式(5),f是相角θ和逆多项式系数a3的函数,可以改写成:

其中:g(θ)和 H(θ)可以分别表示为

可见,系数 a3的可行范围主要是由函数g(θ)的取值确定的。考察g(θ)发现,g(θ)具有如下性质:

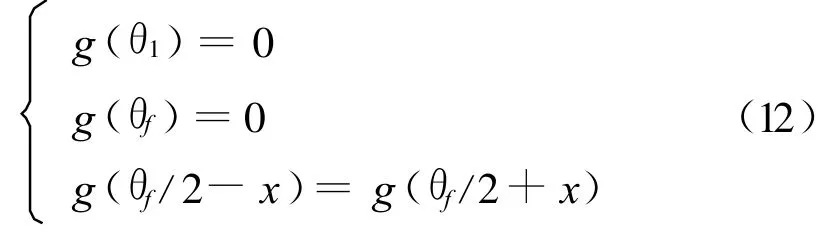
进一步分析可知函数g(θ)实根个数n随转移相角θf的变化特点为:

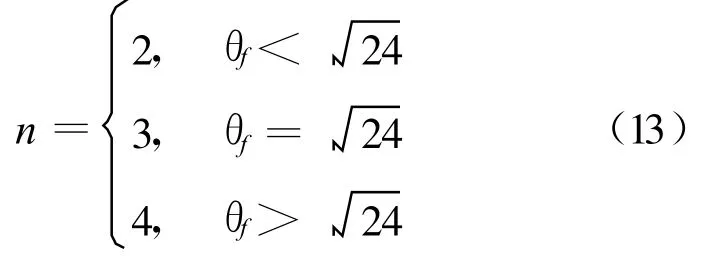
根据以上讨论,针对不同的转移相角,为了保证逆多项式函数(3)描述的轨道满足动力学要求,系数a3实际的可行范围可选定为:

图1 函数 g(θ)与θf的关系Fig.1 Relation between g(θ)and θf

其中:θ′为g(θ)在区间[0,θf]的实根,xmin和 xmax分别为

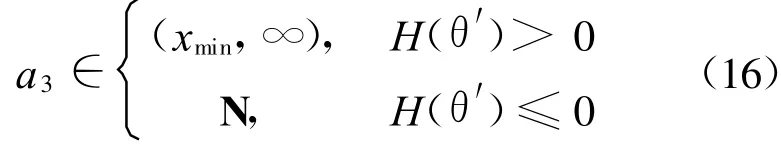
其中:x min可以表示为

其中:xmin可以表示为

根据确定的可行范围,图2给出了逆多项式曲线描述轨道的飞行时间随a3的变化曲线。

由图2可以看出,转移时间 ΔT随系数a3具有良好的单调递减关系。因此,对于给定的发射时间和到达时间,采用逆多项式逼近轨道时只存在无解和单解两种情况,为保证计算的高效性,避免搜索过程中的冗余计算,可首先通过式(20)判断是否有解:

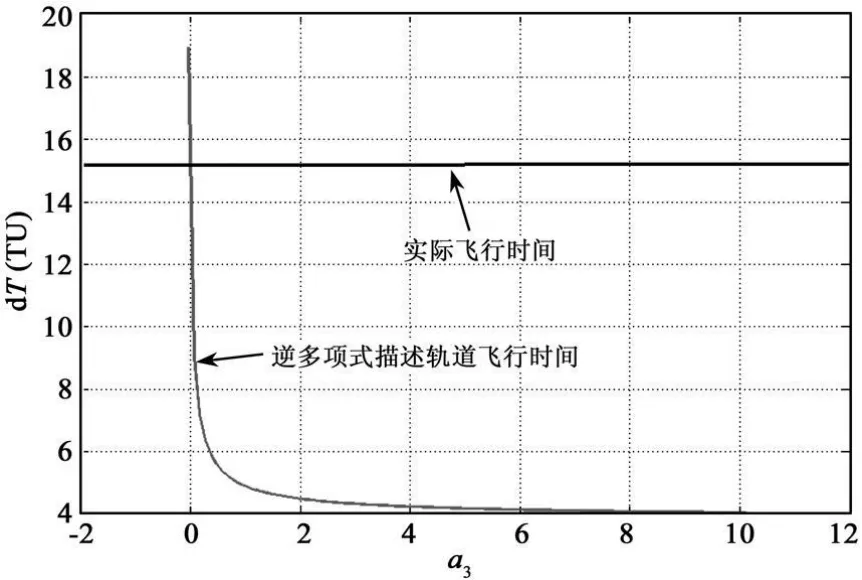
图2 飞行时间随a3的变化曲线Fig.2 Relation betweenΔT and a3

其中:amin3和amax3分别为系数a3的取值上下限,δ为避免ΔT奇异的常值参数,这里取为δ=10-4。

根据确定的可行范围,如果E＞0,则不存在可行轨道,如果 E≤0,则存在可行轨道,采用Brent算法可以简单的寻找到满足时间飞行时间的系数 a3,并且在迭代过程中不会出现˙θ＜0的情况。

3 轨道设计方法

在上述理论研究基础上,本文发展了一种基于逆多项式逼近的行星际轨道初始化设计方法。

3.1 轨道初始设计模型

基于逆多项式逼近理论,燃料最省星际小推力转移轨道设计问题可以描述如下:寻求最优的发射时间 t1、到达目标星体时间t2和转移圈数 nrev,使性能指标(21)达到最小。

这里,寻优参数可以表示为:

F(θ)为转移过程中的加速度,可以表示为:

此外,由于逆多项式理论是在加速度大小可调且无界假设下推导的。为了满足实际的推进器模型,转移过程中加速度大小必须满足如下约束条件:

其中:Fmax为推进器能够提供的最大加速度。

方程(24)描述的约束可看作是寻优问题的路径约束,为无限维的连续约束,为便于计算,可简化为如下一维形式:

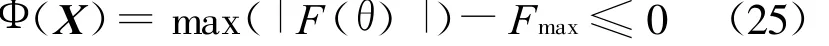
综上所述,基于逆多项式逼近理论,星际小推力转移轨道设计问题可以转化为一个带有整数变量nrev的混合非线性规划问题。

3.2 微分进化算法

本文采用微分进化(DE)算法对归结的混合非线性规划问题进行求解。微分进化是由Storn和Price提出的一种新颖的基于达尔文进化理论的随机搜索算法[7]。与遗传算法相比,微分进化是基于双精度实数编码,并且可以选择采用多种不同变异和选择策略,因此,具有更强的自适应能力,DE算法具体步骤参考文献[7]。

值得注意的是,由于微分进化没有约束处理机制,为此,这里采用模拟退火罚函数策略将混合非线性规划问题转化为无约束优化问题,构造新的性能指标为:

其中:T为退火因子,随着迭代进行由初始温度 T0变化到凝结温度 Tf,其递推公式如下:

采用微分进化求解小推力转移轨道问题的另一个关键问题就是迭代的终止条件,如果微分进化已经寻找到最优解或者已经对当前解不能有所改善,则都应该对优化程序进行终止。微分进化算法作为一种随机非确定算法,每一次运行结果并不相同,因此,必须针对以上两种情况给出合理的终止条件。本文中作者采用如下终止策略:

其中:ε为提前定义的收敛参数,本文中选取ε=10-5,在每一步迭代过程中,优化程序都将记录所有群体中的最优性能指标,当迭代次数G＞15时,优化程序根据式(26)计算性能指标的改善情况,如果满足式(28),则终止优化程序,否则继续迭代。

4 数值仿真与分析

为了充分验证作者对逆多项式理论改进以及所提转移轨道初始设计方法的有效性,这里将给出两个仿真算例。算例1将以固定时间地球-火星的转移为例,验证作者所提改进拟多项式理论的正确性,算例2将以非固定时间地球-水星的转移为例,验证所提轨道初始设计方法的有效性。

4.1 固定时间地球火星交会任务

在算例1中,假定探测器2015年1月1日从地球发射,飞行500天后与火星成功交会,探测器转移过程中绕太阳圈数nrev=1。针对以上问题,采用逆多项式方法求解的结果如表1所示。

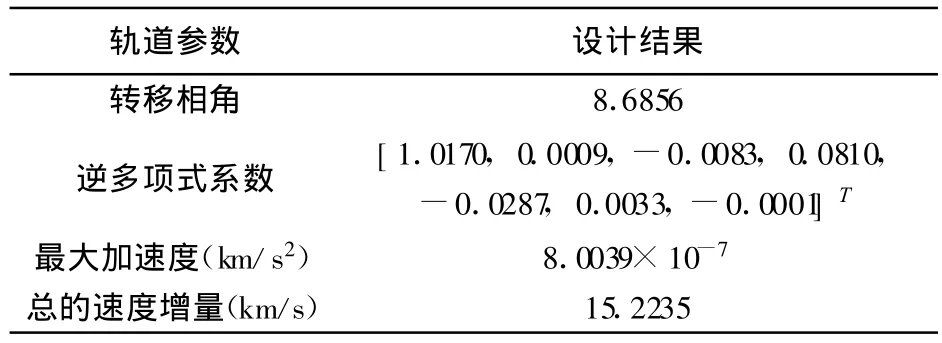
表1 地球-火星转移轨道设计结果Table 1 Design result of Earth-Mars transfer trajectory

针对这一问题,采用文献[6]所给方法进行求解时,无法得到可行的解。这是因为,由于文献[6]中没有给出搜索参数的可行范围,只简单的令其初值为零进行计算,导致搜索过程中参数a3跳出其可行范围,得到的飞行时间为虚值,不满足要求。由此可见,采用改进后的拟多项式逼近理论,可以有效避免传统算法的失效情况,提高逆多项式逼近理论的鲁棒性。图3给出了采用改进逆多项式逼近理论求得的转移轨道示意图。

图3 地球-火星的转移轨道Fig.3 Earth-Mars transfer trajectory

4.2 非固定时间地球金星交会任务

在算例2中,将以非固定时间地球-金星的燃料最省交会任务为例对所给的轨道初始设计方法进行验证。金星探测任务的约束条件如表2所示。微分进化算法参数设置如表3所示。

针对该问题,微分进化算法迭代81步达到了收敛,即满足式(27)给出的终止条件。图4给出了地球-金星转移轨道的性能指标随发射时间和到达时间的分布情况。

表2 地球-金星探测任务约束Table2 Mission constraints of Earth-Venus transfer

表3 微分进化算法参数设置Table3 Parameters set of DE algorithm

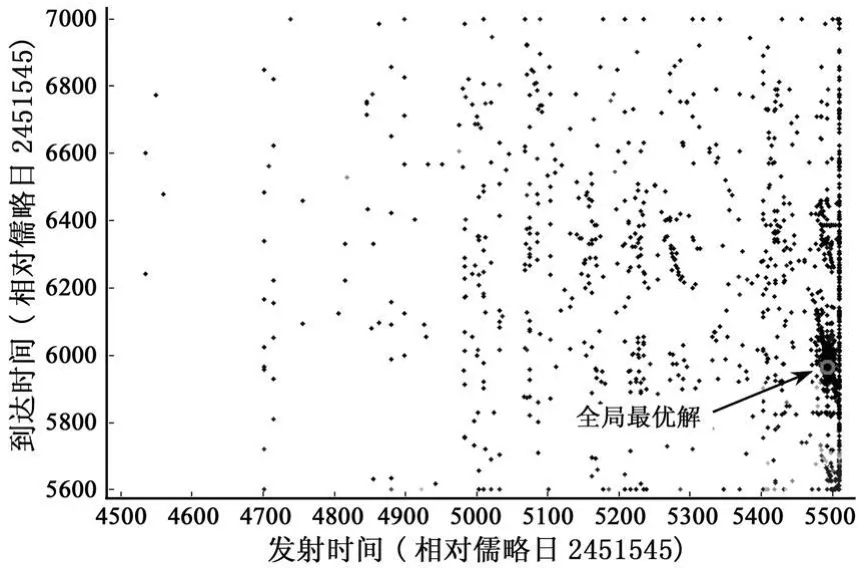
图4 地球-金星转移轨道解空间分布Fig.4 Solution space for Earth-Venus transfer

为验证设计结果的有效性,作者针对该问题,采用高斯伪光谱配点法进行了精确优化[8]。优化过程中,探测任务的约束条件同表2,探测器采用平面运动方程,假设推力大小和方向都可调,性能指标取为式(21)。高斯伪光谱配点算法的离散点数取为50,则优化问题有302个寻优参数,250个约束条件。两种求解方式的计算结果如表4所示。

表4 计算结果比较Table 4 Comparison between two algorithms

由表4可以看出:(1)采用作者所提的基于微分进化的初始设计方法,设计结果与高斯伪光谱方法的结果较为接近,其中从地球发射时间与最优解仅相差6天,飞行时间相差8.733天,所需要的总的速度脉冲相差约1.24%,同时,初始设计方法求得轨道的最大推力约束为0.25N,完全满足任务约束,这充分表明作者所提的设计方法是有效的,可以获得满足任务约束的次优转移轨道;(2)从另一个角度,既然初始设计方法的设计结果与高斯伪光谱方法得到的最优解差别很小,也表明了初始设计方法获得的次优解可以为精确的转移轨道设计提供可行有效的设计初值。由此可以看出,作者所给的行星际小推力转移轨道初始设计方法是行之有效的,采用其获得的初值猜测可以大大降低行星际小推力转移轨道的设计难度。为了充分比较作者所提算法与高斯伪光谱所获的最优解,图5和图6分别给出了两种算法获得的转移轨道示意图和推力大小时间历程。

图5 地球-金星转移轨道示意图Fig.5 Earth-Venus transfer trajectory

由图5和图6可以看出,两种算法获得的转移轨道和推力大小时间历程尽管存在一定差别,但总体趋势是一致的,这进一步验证了作者所给设计方法的正确性和有效性。造成两种算法所获轨道差别的主要原因是:在逆多项式逼近算法中,假定推力方向始终沿速度方向或其反方向,而在高斯伪光谱方法中,认为其推力方向是自由可调的。

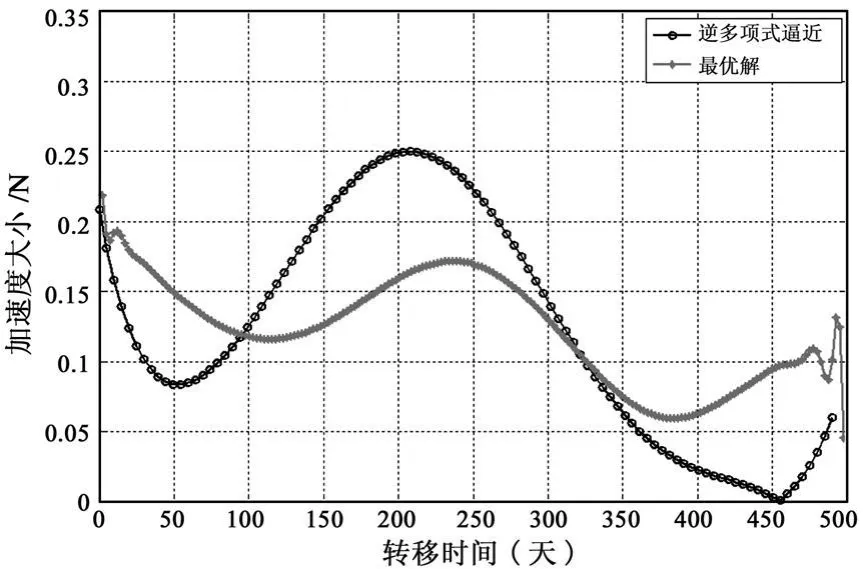
图6 推力大小时间历程Fig.6 Time history of thrust magnitude

5 结 论

针对行星际小推力转移轨道初始设计问题,提出了一种基于改进逆多项式逼近的设计方法。该方法具有以下三个优点:(1)推导了关键系数的动力学可行范围,相比传统拟多项逼近算法具有更高的鲁棒性;(2)所提设计方法的模型简单,设计参数少;(3)采用结合微分进化与模拟退火的寻优算法,可以快速有效获得逆多项式逼近下的全局最优解。作者所提初始设计方法可为精确设计提供行之有效的初值,从而有效提高行星际小推力转移轨道的设计效率,降低其设计难度。本文的研究可以为行星际小推力探测任务的设计与规划提供有价值的参考。

[1] Bertrand R,Bernussou J,Geffroy S.Electric transfer optimization for mars sample return mission[J].Acta Astronautica,2001,48(5-12):651-660.

[2] Strange N J,Longuski JM.Graphical method for gravity-assist trajectory design[J].Journal of Spacecraft and Rockets,2002,39(1):9-16.

[3] Pascale D P,Vasile M.Preliminary design of low-thrust multiplegravity-assist trajectories[J].Journal of Spacecraft and Rockets,2006,43(5):1065-1076.

[4] Petropoulos A E,Longuski JM.Shape-based analytic representations of low-Thrust trajectories for gravity-assist applications[C].AAS/AIAA Astrodynamics Specialist Conference,16-19August 1999:1-19.

[5] Petropoulos A E,Longuski JM.Shape-based algorithm for automated design of low-thrust,gravity-assist trajectories[J].Journal of Spacecraft and Rockets,2004,41(5):87-796.

[6] Wall B J,Conway B A.Shape-based approach to low-thrust rendezvous trajectory design[J].Journal of Guidance,Control,and Dynamics,2009,32(1):95-101.

[7] Storn R,Price K.Differential evolution:Asimple and efficient adaptive schemefor global optimization over continuous spaces[R].Technical Report TR-95-012,Berkeley,USA,1995.

[8] Benson D.A gauss pseudospectral transcription for optimal control[D].Department of Aeronautics and Astronautics,MIT,2004.