一种新的脉冲星累积脉冲轮廓辨识算法

苏 哲,王 勇,许录平,罗 楠

(西安电子科技大学电子工程学院,西安710071)

0 引 言

X射线脉冲星导航(XPNAV:X-ray Pulsar-based Navigation)是一种新的天文自主导航技术,可为近地轨道、深空和星际空间飞行的航天器提供精确的位置、速度、姿态和时间等导航信息。利用观测信号辨识脉冲星是XPNAV的重要环节[1]。根据辨识结果从星载导航数据库中提取该脉冲星的辐射方向,可推出航天器的姿态;已知航天器姿态定向观测某颗脉冲星时,也需要根据辨识结果来验证姿态的正确性和准确度[2];根据脉冲星类型从导航数据库中提取其发射频率,与实测脉冲频率比较,测定多普勒频移量,可计算航天器在脉冲星视线上的运动速率;根据脉冲星类型提取导航数据库中的标准轮廓和星历等参数,测量脉冲到达时间,可解算出航天器在三维空间中的位置[3]。因此,在有限的观测时间内,快速、准确的辨识脉冲星对于航天器定姿、测速和定位都具有重要意义。迄今为止发现的脉冲星中,没有哪两颗具有完全相同的形成过程和辐射机理,所以可通过周期和累积脉冲轮廓唯一确定一颗脉冲星。但是,在轨航天器观测的脉冲星信号十分微弱,且受到多普勒效应和噪声的影响,测量所得周期值存在误差[4],同时,许多适于XPNAV的毫秒脉冲星的周期非常接近,故采用周期辨识难以取得良好的辨识效果。累积脉冲轮廓被认为是脉冲星极冠区的辐射窗口,这种由物理性质所决定的信号特征极其稳定。因此,XPNAV系统中可通过比较累积脉冲轮廓和导航数据库中的标准轮廓辨识脉冲星编号。

通过累积脉冲轮廓辨识脉冲星的基础是特征向量的提取。由于叠加起始时刻不同,累积脉冲轮廓和标准轮廓间存在相位差,这要求特征向量具有平移不变性。同时,在XPNAV系统中,由于多普勒效应、相位间隔的不同和脉冲周期测量的不准确性,累积脉冲轮廓相对于标准轮廓还存在尺度伸缩。综上所述,在XPNAV系统中通过累积脉冲轮廓辨识脉冲星,提取累积脉冲轮廓中具有平移和尺度伸缩不变性的特征信息,并抑制噪声,是解决问题的关键。

现有的射电脉冲星累积脉冲轮廓辨识算法主要有一维选择线谱算法[5]。该算法在选择双谱辨识算法[6]的基础上,改进了特征向量的降维方法。这两种辨识算法均利用双谱的平移不变性提取特征信息,并抑制高斯噪声,辨识效果相差不大。由于双谱不具有尺度伸缩不变性,这两种算法均无法有效辨识具有尺度伸缩效应的累积脉冲轮廓,不适于XPNAV系统。

针对XPNAV系统中累积脉冲轮廓的辨识问题,本文在双谱的基础上,引入Mellin变换,提出了一种基于选择Bispectra-Mellin(BM)谱的累积脉冲轮廓辨识算法。该算法通过BM变换提取累积脉冲轮廓中的平移和尺度伸缩不变特征信息,并滤除噪声,然后利用简化的Fisher可分离度对BM幅度谱降维,提取特征向量,用于相关辨识。该算法能有效抑制累积脉冲轮廓的平移、尺度伸缩和噪声对辨识的影响,运算量小,适用于XPNAV系统。

1 XPNAV系统中累积脉冲轮廓的特点分析

RXTE(Rossi X-ray Timing Explorer)是美国NASA探索者系列卫星中具有高时间分辨率(1μs),大有效面积(6250 cm2)和宽能谱范围(2-200keV)的X射线探测器,具有对突发现象迅速反应并实施探测的能力,适于对X射线脉冲星进行观测研究。本文从美国高能天文数据中心(HEASARC:High Energy Astrophysics Science Archive Research Center)获取RXTE的脉冲星观测数据进行研究。数据的提取和初步处理采用HEASARC提供的专用工具包FTOOLS。

以脉冲星B0531+21为例,滤除RXTE的无效观测数据后,进行时间转换,周期叠加,得到该脉冲星的标准轮廓(累积时间略大于7小时,相位间隔设为2.8125度),如图1所示。其脉冲宽度比(半高宽度与周期的比值)为43.12%。

图1 脉冲星B0531+21的标准轮廓,相位间隔为2.8125度Fig.1 Thestandard profile of pulsar B0531+21,the phasebin is 2.8125 degree

模拟XPNAV系统中的情况,假设未知观测信号的脉冲星类型,利用FTOOLS工具包中的Powspec工具估计其自转频率,并设自转频率的1、2阶导数均为零。截取一段10秒种的观测数据,进行光子到达时间的转换后,将相位间隔设为2.8125度,进行周期叠加。由于RXTE的轨道数据更新时间为60秒,所以时间转换无法消除10秒内卫星运动引起的多普勒效应。所得累积脉冲轮廓如图2(a)所示。计算其脉冲宽度比为43.58%。利用标准轮廓计算其信噪比为9.43dB。对比图1和2(a)可看出,航天器高速运动引起的多普勒效应和对信号叠加时采用的周期不准确,导致累积脉冲轮廓略微展宽,相对于标准轮廓的尺度伸缩幅度为0.989。

图2 脉冲星B0531+21累积脉冲轮廓,累积时间10秒,相位间隔分别为2.8125度(a)和7.2度(b)Fig.2 Theintegrated pulse profile of pulsar B0531+21,theintegrated time is 10 seconds,and thephase bin is 2.8125 degree(a)and 7.2 degree(b)respectively

将相位间隔设为7.2度,其他条件不变,进行周期叠加,所得累积脉冲轮廓如图2(b)所示。其信噪比为11.21dB,相对于标准轮廓的尺度伸缩幅度为2.53。对比图2(a)和2(b),在相同的累积时间下,2(b)具有较长的相位间隔,单个相位间隔内的累积时间较长,其信噪比高于2(a)。因此,适度延长相位间隔虽然会导致累积脉冲轮廓产生尺度伸缩,但却能大幅度提高其信噪比。换句话说,如果能找到一种可屏蔽尺度伸缩的方法,就能够极大地缩短辨识所需累积脉冲轮廓的叠加时间,从而缩短整个XPNAV系统导航参数的输出时间间隔。

Taylor所建立的射电脉冲星累积脉冲轮廓模型[7]中,将累积脉冲轮廓看作是标准轮廓时延和加噪后的结果。但是,图2所示累积脉冲轮廓除受到上述因素影响外,也产生了尺度伸缩,伸缩幅度分别为0.98和2.53。为准确描述累积脉冲轮廓相对于标准轮廓的尺度伸缩,引入尺度因子,将其表达式改为:

上式中,a为直流偏差,b为幅度因子,f(t)为标准轮廓,g(t)为噪声,服从Poisson分布,d为时间延迟,s为尺度因子。

由(1)式可知,通过比较累积脉冲轮廓p(t)和导航数据库中的标准轮廓f(t)来辨识脉冲星,辨识算法必须能够屏蔽时间延迟(d)和尺度(s)上的差异,提取具有平移和伸缩不变性的特征信息,并抑制噪声g(t)。

2 基于选择BM谱的脉冲星累积脉冲轮廓辨识算法

2.1 Bispectra-Mellin变换及其平移和尺度伸缩不变性

实信号x(t)同其伸缩量x(st)的Mellin变换为:

可见,信号x(t)尺度的变化仅仅导致其Mellin变换的相位发生变化,而对幅值没有影响。本文对两维信号x(t1,t2)的Mellin变换做出如下定义:

尺度伸缩后的信号x(s1 t1,s2 t2)的Mellin变换为:

可见,(4)式所定义的两维Mellin变换的幅值同样具有伸缩不变性,可用于提取信号中的尺度伸缩不变特征量。

借鉴一维Mellin变换的实现方法——DMT算法[8],本文给出一种两维Mellin变换的实现方法。假设x(t1,t2)在很小的积分区域{(t1,t1+Δt),(t2,t2+Δt)}内为常量,则可将(4)式展开为:

为提取平移和尺度伸缩不变特征量,并抑制噪声的影响,本文将两维Mellin变换和双谱相结合,给出实信号x(t)的Bispectra-Mellin变换的定义:

其中,max(·)为取极大值运算符,用于对双谱幅度进行归一化,消除幅度因子 b对辨识的影响。B(ω1,ω2)是信号 x(t)的双谱。

文献[9]指出,当每个相位间隔中的光子数均大于20时,Poisson噪声g(t)近似服从零均值Gaussian分布。理论上,Gaussian过程的双谱为零。因此,假设p(t)中直流分量 a已经滤除,且累积时间足够长使得每个相位间隔中光子数均大于20,易知信号f(t)和p(t)的双谱间有如下关系:

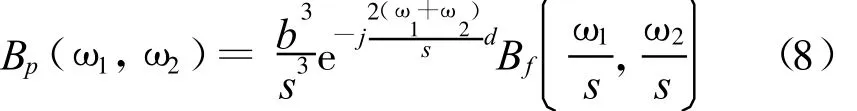
结合(7)式,可得f(t)和p(t)的BM谱间关系为:

可知,BM幅度谱具有平移和尺度伸缩不变性,且继承了双谱抑制噪声的能力,适用于在XPNAV系统中提取脉冲星累积脉冲轮廓的特征信息。

2.2 BM幅度谱的降维

由于BM幅度谱维数较高,不利于辨识,需对其进行将维处理。降维的过程本质上是从高维的BM幅度谱中选择最能代表不同类型脉冲星间差异的点,组成特征向量。现有辨识算法中,降维的方法主要有Fisher可分离度方法[6]和一维选择线谱方法[5]。在实验中发现,一维选择线谱方法的运算量极大,星载计算机运算能力有限,难以利用该算法实时地辨识脉冲星信号。因此,本文仍采用Fisher可分离度方法对BM幅度谱降维,并针对脉冲星的特点对Fisher可分离度进行了适当简化,使之更适于XPNAV系统。

脉冲星标准轮廓是脉冲星极冠区的辐射窗口,在软X射线频段标准轮廓具有唯一性。因此,在提取特征向量时,每类脉冲星信号仅需一个训练样本——由长时间观测数据叠加所得标准轮廓。此时,仅需寻找能使不同类别间差异最大的若干点组成特征向量,即可取得良好的辨识效果。

假定 {M(i)(ρ1,ρ2)}i=1,2,…,I是训练样本集合的BM变换幅度谱,其中上标 i表示不同编号的脉冲星,I表示训练样本集合中脉冲星的种类数目。该训练样本集合在(ρ1,ρ2)点的可分离度定义为:

根据上式,计算BM谱域内所有点的 m(ρ1,ρ2),选择具有最大 m(ρ1,ρ2)值的 N个点组成特征向量,即可有效辨识该训练样本内的脉冲星。

实验中发现,N的取值非常重要,N太小,特征向量不足以涵盖该训练样本集合中所有脉冲星标准轮廓的特征信息,导致辨识效果不佳;N太大,特征向量包含了不同类标准轮廓间的共有信息,不仅不能提高辨识效果,还会增加运算负担。

为确定N的取值,定义一种衡量辨识效果的性能指标——可辨识度。累积脉冲轮廓的可辨识度r定义为:

其中,corc为脉冲星累积脉冲轮廓和其标准轮廓特征向量的相关系数,corm为累积脉冲轮廓和训练样本中其它类型脉冲星标准轮廓的特征向量相关系数的最大值。易知,r＞1时,根据该累积脉冲轮廓可得出正确的辨识结果,且 r越大,辨识效果越好,抗干扰能力越强;r≤1时,无法得到正确的辨识结果。

实验中,对于选定的训练样本,首先令 N=2,计算脉冲星的可辨识度;增加N的取值,可辨识度也不断提高;当N大于N0时,继续增加N的值时,可辨识度不再有明显提高,有时还会略微减小。此时,对于该训练样本,可取N=N 0。

3 实验与结果分析

实验数据由RXTE观测得到,取自HEASARC数据库,数据格式为FITS(Flexible Image Transport System)。实验工作在Matlab7.04环境下完成。

3.1 累积脉冲轮廓的BM变换

分别计算图1所示标准轮廓和图2(b)所示累积脉冲轮廓的双谱和BM幅度谱,如图3、4所示。在计算双谱变换时,为抑制噪声,在双谱域加入Rao-Gabr平滑窗[10],窗口长度设为5倍于采样周期。在计算两维Mellin变换时,根据双谱的对称性,仅取双谱域右上角1/4区域的点参与计算,可在降低运算量的同时不丢失特征信息。

对比图3(a)和4(a)可以看出,标准轮廓和累积脉冲轮廓(尺度因子2.53,信噪比11.21)的双谱具有相似性,但尺度不同,说明双谱变换不具有伸缩不变性。对比图3(b)和4(b)可以看出,BM幅度谱图形相似,且矫正了双谱尺度上的差异,说明BM变换具有平移和尺度伸缩不变性。

图3 脉冲星B0531+21标准轮廓的双谱幅度谱(a)和BM幅度谱(b)的等高线图Fig.3 The contour line of bispectra(a)and BM spectra(b)amplitude of the standard profile of pulsar B0531+21

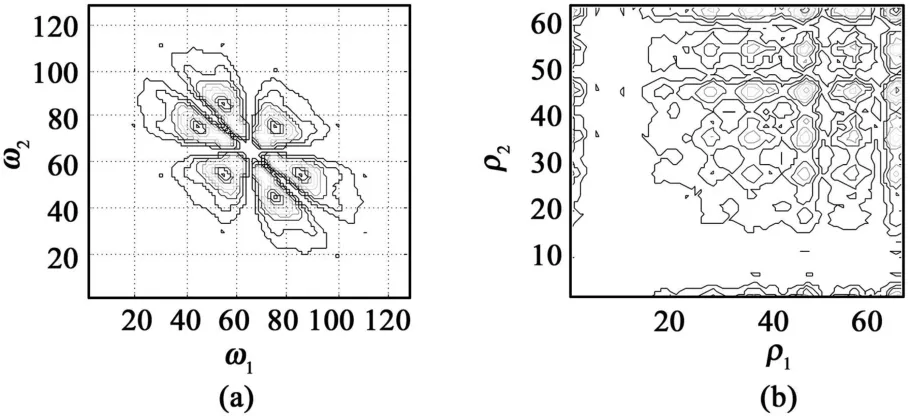
图4 脉冲星B0531+21累积脉冲轮廓的双谱幅度谱(a)和BM幅度谱(b)的等高线图Fig.4 The contour line of bispectra(a)and BM spectra(b)amplitude of the integrated pulse profile of pulsar B0531+21

3.2 辨识实验

选择双谱算法和一维选择线谱算法均是利用双谱的平移不变性提取特征信息。通过图3(a)和4(a)可知,无论采用什么样的降维方法,均很难通过双谱域上的特征向量辨识不同尺度的累积脉冲轮廓。下面将进一步通过比较选择双谱算法和本文算法的辨识效果说明该问题。

从文献[11]列出的适于导航的脉冲星(具有较高品质因子)中选择12颗已被RXTE观测过的脉冲星 :B1929+10、B1055-52、B1046-58、B1323-62、B0531+21 、B1713-40 、B1719-37 、B1742-30 、B1749-28、B1821-24、J1730-2304 和 J1617-5055,按照先后顺序,其编号分别为1～12。将相位间隔均设为2.8125度,长时间累积得到它们的标准轮廓,作为训练样本集合。

分别计算训练样本集合中各标准轮廓的BM幅度谱。然后,利用(10)式计算BM谱域内每个点的可分离度。对于该训练样本,取N=10。提取具有最大可分离度的10个点作为标准轮廓的特征向量。待辨识信号仍选用B0531+21的累积脉冲轮廓,累积时间10秒,相位间隔7.2度,相对于标准轮廓的尺度因子2.53,每个相位间隔中的光子数均大于300,噪声服从高斯分布。计算其BM幅度谱,并从中提取特征向量。分别计算该特征向量与训练样本集合中所有标准轮廓特征向量的相关系数,结果如图5中实线所示。其中,横坐标表示脉冲星编号。图5中虚线为通过选择双谱算法提取脉冲星标准轮廓和累积脉冲轮廓的特征向量,进行相关运算的结果。

图5 脉冲星B0531+21累积脉冲轮廓的特征向量与训练样本集合中标准轮廓特征向量的相关系数Fig.5 The feature vectors correlation coefficients of theintegrated pulseprofileof B0531+21 and standard profiles in training set

可以看出,当尺度因子 s≠1时,BM幅度谱所提取的累积脉冲轮廓的特征向量和其标准轮廓的特征向量具有较高的相关性,可用于辨识脉冲星类型;反观选择双谱算法,由于双谱不具有尺度伸缩不变性,相同类型脉冲星的累积脉冲轮廓和标准轮廓的特征向量的相关性较低,难以用于辨识。

3.3 相位间隔长度对辨识效果的影响

为讨论相位间隔长度与辨识效果的关系,分别计算具有不同相位间隔的累积脉冲轮廓的可辨识度。训练样本集合仍采用前一节中列举的12颗脉冲星的标准轮廓。对B0531+21的同一段观测数据(10秒钟)进行周期叠加,设置不同的相位间隔,可得不同尺度因子和信噪比的累积脉冲轮廓,分别计算它们的可辨识度,如表1所示。

可以看出,选择双谱算法仅当尺度因子近似为1时,可辨识度略大于1;而本文算法对于不同的尺度因子,均可有效辨识。而且随尺度的增加,可辨识度总体上有提高的趋势。这与增加相位间隔长度使累积脉冲轮廓的信噪比增加相吻合。但是,当相位间隔长度过大时(大于等于9),由于累积脉冲轮廓无法提供足够多的可供辨识的信息,可辨识度小于1。当相位间隔为4.8度时,可辨识度最高,此时累积脉冲轮廓不仅能提供足够多的辨识信息而且信噪比较高。

表1 不同相位间隔的累积脉冲轮廓的可辨识度Table 1 The recognition rateof the accumulated pulse profileswith different phase bin sizes

3.4 运算量分析

下面从运算量的角度考察本文算法。实验用计算机基本配置为Intel双核2.2GHz CPU,2GDDR2内存。表2对比了选择双谱算法和本文算法所耗时间。

表2 选择双谱和本文算法耗时对比Table2 The comparison of consuming time between selected bispectra algorithm and the proposed algorithm

在标准轮廓特征向量的提取阶段,需分别计算训练样本在BM谱域上每个点的可分离度,然后从中选择具有最大可分离度的若干点作为特征向量。该阶段运算量较大,但为前期准备阶段,并不影响算法的实时性,因此可选择经长时间累积、具有高信噪比、一个周期内有较多相位间隔的标准轮廓作为训练样本集合。对累积脉冲轮廓的辨识阶段,仅需计算累积脉冲轮廓BM变换的若干点,组成特征向量,并依次与已经存储于计算机内存中的标准轮廓特征向量进行相关匹配,运算量较小。本文算法与选择双谱算法相比,需另外计算若干点的两维Mellin变换,故其辨识阶段的运算量略大于选择双谱算法,但毫秒级的辨识时间同脉冲星信号的累积时间(本实验中为10 s)相比,几乎可忽略不计。

4 结 论

在有限的观测时间内,快速、准确的辨识脉冲星类型对于利用X射线脉冲星定姿、测速和定位具有重要意义。本文研究了XPNAV系统中累积脉冲轮廓的特点,针对XPNAV系统提出了一种基于选择BM谱的脉冲星累积脉冲轮廓辨识算法。理论分析和实验结果表明:(1)BM幅度谱具有平移和尺度伸缩不变性,且能抑制噪声;(2)本文算法可有效辨识具有平移和尺度伸缩效应的累积脉冲轮廓,辨识效果优于现有辨识算法;(3)利用相同的观测数据,通过合理选择相位间隔的长度(4.8度),本文算法能够达到最佳可辨识度;(4)本文算法运算量小,适用于XPNAV系统。

[1] SHEIKH S I.The use of variable celestial X-ray sources for spacecraft navigation[D].Maryland:Maryland University,2005.

[2] SHEIKE SI,PINES D J.Spacecraft navigation using X-ray pulsars[J].Journal of Guidancecontrol and dynamics,2006,29(1):49-63.

[3] 帅平,陈绍龙,吴一帆,等.X射线脉冲星导航原理[J].宇航学报,2007,28(6):1538-1543.[SHUAI Ping,CHENG Shaolong,WU Yi-fan,et al.Navigation principles using X-ray pulsars[J].Journal of Astronautics,2007,28(6):1538-1543.]

[4] 苏哲,许录平,王光耀,等.基于离散方波变换的脉冲星微弱信号周期性检测[J].宇航学报,2009,30(6):2243-2248.[SUZhe,XULu-ping,WANGGuang-yao,et al.Pulsar weak signal periodicity detection based on discrete square wave transform[J].Journal of Astronautics,2009,30(6):2243-2248.]

[5] XIEZheng-hua,XU Lu-ping,NIGuang-ren,et al.A new feature vector using selected line spectra for pulsar signal bispectrum characteristic analysis and recognition[J].Chinese Journal of Astronomy and Astrophysics,2007,7(4):565-571.

[6] ZHANG Xian-da,YUShi,BAOZheng.A new feature vector using selected bispectra for signal classification with application in radar target recognition[J].IEEE Trans.on Signal Processing,2001,49(9):1875-1885.

[7] Taylor JH.Pulsar timing and relativistic gravity[J].Class.Quantum Grav,1993,10:S167-S174.

[8] Zwicke P E,Kiss I.A new implementation of the mellin transform and its application to radar classification of ships[J].IEEE Trans.on Pattern Analysis and Machine Intelligence,1983,5(2):191-198.

[9] Hanson J,Sheikh S,Graven P,et al.Noise analysisfor X-ray navigation systems[C].2008 IEEE/ION Position,Location and Navigation Symposium,Monterey,USA:IEEE,2008:704-713.

[10] Nikias C L,Petropulu A P.Higher-order spectra analysis[M].New Jersey:PTRPrentice-Hall,1993.

[11] Josep Sala,Andreu Urruela,Xavier Villares.Feasibility study for a spacecraft navigation system relying on pulsar timing information final report[R].Technical University of Catalonia Final Report for ARIADNA project 03/4202,2004.