图像置乱技术综述

谭永杰 ,张文娟 ,崔海花

(1.周口师范学院计算机科学系,河南周口466001;2.周口科技职业学院,河南周口466000)

图像置乱作为一种信息隐藏技术,虽然起步不早,但由于各方面的财政支持,近年来该技术的发展速度很快,这与它在实际应用中所发挥的巨大作用是分不开的。随着多媒体技术、信息存储技术的飞速发展,以及网络带宽限制的放松,越来越多的数字图像得以在网络上传输,并逐步成为人们获取信息的主要手段。网络上传输的数字图像有些涉及到个人隐私或公司利益;有些甚至是军事机密,牵涉到国家的安全,是至关重要的。所以,对传输的数字图像进行可靠的加密处理,越来越引起众多学者的关注。并逐步产生了图像置乱技术,提出了很多种图像置乱算法。纵观这些算法,从大的方面可以分为两种:基于位置空间的置乱和基于色彩空间的置乱,有些则是将这两种方法结合以求得更好的置乱效果。本文按照所依据的置乱原理分别介绍这两种置乱方法中的一些经典算法,并深入分析其置乱原理。

1 图像置乱的概念与分类

1.1 图像置乱的概念

根据资料,图像置乱的定义可归纳为以下两种[1]:

定义1 给出图像A=[a(i,j)]nXm,变换矩阵T=[t(i,j)]nXm是1,2,…,n X m的一种排列,用T作置乱变换,得到图像B。其变换方法如下:

将A与T按行列作一一对应,将A中对应位置1的像素灰度值(或RGB分量值)移到对应位置2,对应位置2的像素灰度值移到对应位置3,以此类推。最后将对应n X m位置的像素灰度值移到对应位置1,就得到了按T置乱后的图像B。称图像A经置乱变换T变换到了图像B。记为B=TA。

定义2 给定一幅n X m大小的灰度图像A= [a(i,j)]nXm,假设变换T是{(x,y):1≤x≤n,1≤y≤m,且 x,y均为整数}到自身的一一映射,即

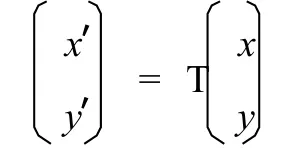
将图像A中位置(x,y)处的元素变换到位置(x′, y′)处,得到图像B,则称变换 T是图像A的置乱变换。仍记为B=TA。

从数学本质上看,上面两个定义没有本质的区别,只是在不同的场合,有的用起来较方便。

1.2 图像置乱的分类

到目前为止,关于图像置乱的算法已经有好多种,从大的方面可分为基于图像位置空间、基于图像色彩空间和基于图像频域空间的置乱;从具体的算法上也有许多成熟的算法被应用到图像置乱中,如基于 A rnold变换[2-4]、幻方变换[5]、Hilbert曲线[6]、队列变换方法[7]等。这些都是基于图像位置空间的经典置乱方法,而继黄石则提出了基于灰度变换的置乱方法后,也陆续有学者尝试着在灰度空间进行置乱,并提出了一些好的置乱方法,如 Gray码[8]、S盒[9]、混沌映射[10]等方法。其置乱思想来源于数字图像处理中的灰度直方图变换,针对图像像素值进行置乱,该方法是基于图像色彩空间的算法。本文主要描述这两种算法中有代表性的方法。

2 位置空间的图像置乱方法

2.1 基于Arnold变换的图像置乱

A rnold变换是A rnold在遍历理论研究中提出的一种变换,俗称猫脸变换,原意为cat mapping。设想在平面单位正方形内绘制一个猫脸图像,通过如下变换

这个猫脸图像将由清晰变模糊,这就是A rnold变换[4]。

式(1)中mod 2表示模2运算。具体到数字图像置乱方面时,x,y表示原图像像素点的位置,x′, y′表示置乱后像素点的位置,mod 2须换成mod N,N是图像矩阵的阶数,对其取模以保证置乱后的像素点的位置不超出图像矩阵下标界限。故式(1)可改写为

一幅图像在经过式(2)后,其位置进行了一对一的换位,从而得到另一幅不相关的图,达到图像加密的目的。

式(1)是标准的cat映射,即系统参数a=1,b=1,c=1,d=2,而丁玮等证明了对于如下2 X 2矩阵[7]

当其元素满足ad-bc=1时,它对平面坐标的变换可作为一类置乱变换。也就是说,当系统参数取值不同,但只要其满足ad-bc=1,得到的置乱图像也会不同,这就加大了图像加密的灵活性。

总之,A rnold变换简单、易实现且具有周期性,即当迭代次数达到某一值时,置乱成原始图像。文献[6]给出了不同阶数 N下数字图像的A rnold变换周期,如表1所示。

观察表1知,A rnold变换的周期性与图像大小有关,但不成正比。

下面以256级的灰度图像lena为实验对象,在Matlab R2007b的环境下,进行仿真实验。经过1次参数为{1,1,7,8}的A rnold置乱变换后得到的置乱图像如图1。

2.2 基于幻方变换的图像置乱

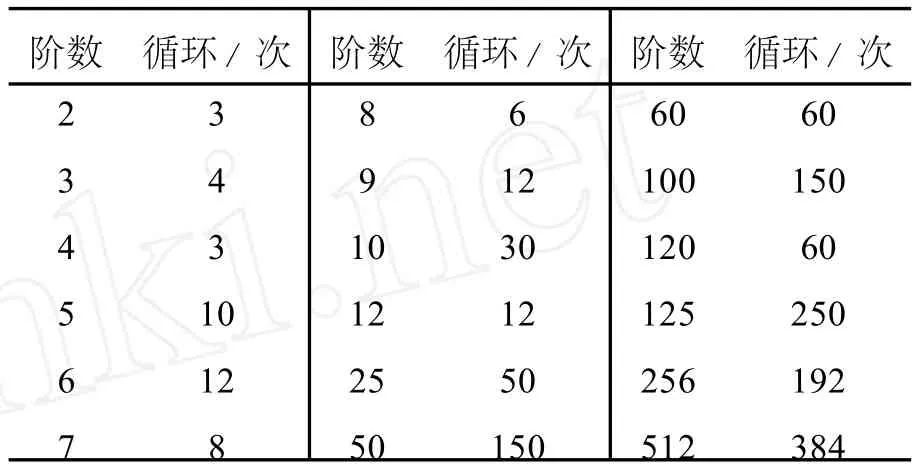
表1 不同阶数 N下数字图像的A rnold变换周期

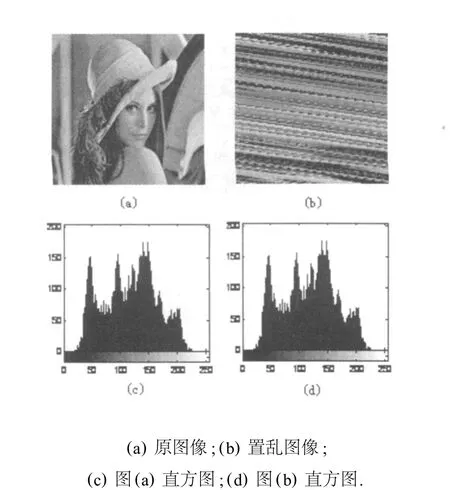
图1 A rnold变换置乱图像及其直方图

幻方(M agic)是非常古老的数学问题。一个 N阶幻方是由整数1,2,3,…,N2按下述方式组成的N X N方阵。该方阵每行、每列、每条对角线上的整数和都等于同一个数 S,这个数叫幻方和[8]。经过古今中外众多数学家的多年潜心研究,已取得丰富的成果。当前,幻方已从被认为仅仅是“奇怪的现象”而逐渐开发了它的应用。事实上,幻方与群论、组合分析、试验设计等分支有许多关联。幻方的潜在价值有待人们去探索和发现。幻方的定义及数学表达式为[11]:以1,2,3,…,N2个自然数为元素构成的N阶方阵

若A中的元素满足

则称A为N阶幻方矩阵,简称 N阶幻方,这里 N为任意整数。

将幻方理论运用到图像置乱中,其置乱方法的流程图见图2。

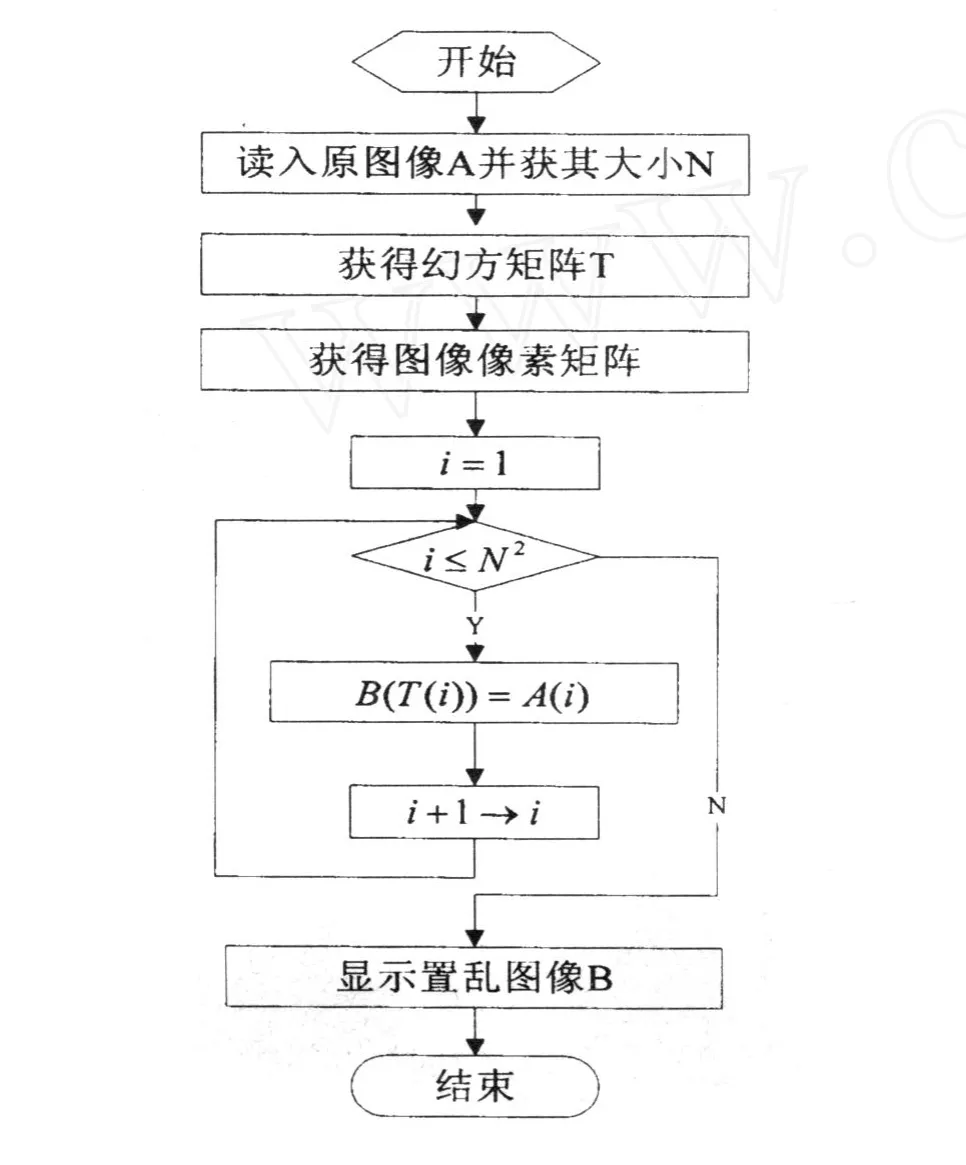
图2 幻方置乱流程图

分析了幻方的原理及其在图像置乱中的应用后,进行了验证性实验,对图1(a)进行置乱,结果见图3。

以上两种均为在位置空间的置乱变换,除此之外,类似的算法还有很多。如针对 A rnold变换、Hilbert曲线变换、Fibonacci变换[11]等置乱算法存在取模运算,在置乱时较为费时,且逆变换不易求得等不足。

3 基于色彩空间的图像置乱方法

与基于位置空间的图像置乱方法相比,在色彩空间对图像置乱得到的图像直方图得到改变,分布均衡,也更加安全。

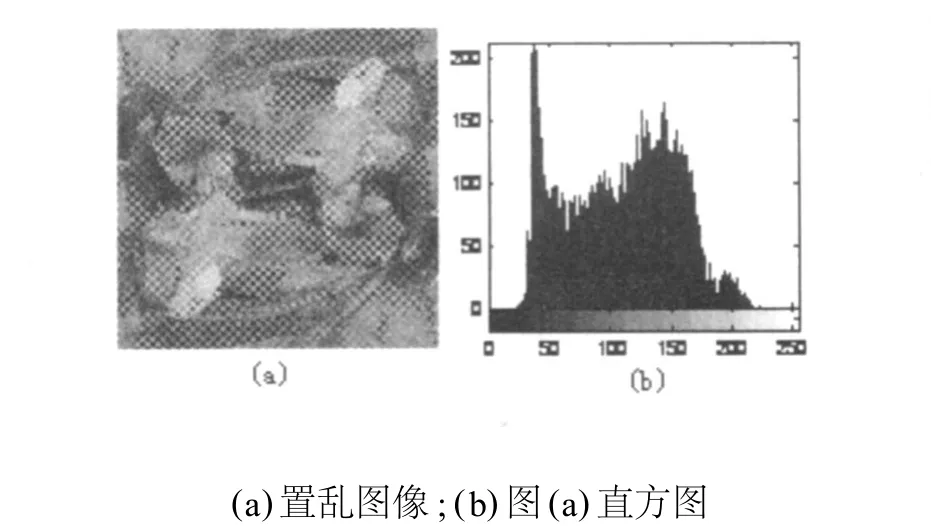
图3 基于幻方的置乱效果图及其直方图

3.1 基于混沌序列的图像置乱

英国数学家M athew s首先提出以Logistic映射作为序列密钥生成器,将混沌系统用于加密。Logistic映射是一类被广泛研究的动力系统,定义为[12]

其中当3.569 945 6<μ≤4时,Logistic映射呈现混沌状态,xn∈(0,1)。

Logistic映射具有确定性,而且具有形式简单、对初值敏感等特点,其序列的遍历统计特性等同于零均值白噪声,具有良好的随机性、相关性和复杂性[13]。利用Logistic映射对初始条件的敏感性可获得数量很大的混沌序列,解决了任意长随机比特序列的生成、传输、存储等无法逾越的难题,可用于数据量大的数字图像置乱方面。在对混沌理论进行分析之后,进行了以下的验证性实验,仍选取图1(a)为待置乱图像,实验结果见图4。

观察图4(b)与图1(c)知,用该方法置乱后直方图发生改变,置乱图像的纹理颗粒更加细腻,但不足之处是仍可依稀看到原图像的轮廓,如再结合位置空间的置乱对其进行预处理,可达到较好的置乱效果。与前面几种基于位置空间的置乱方法相比,从HVS角度来说,效果更优。

3.2 基于Gray码的图像置乱

定义3[8]对于任意非负整数 u,其二进制码记为 u=(upup-1…u1u0)2,令

i=1,2,…,p-1,则得到一个二进制表示的整数变换 g(u)=(gpgp-1…g1g0)2,式(5)称为 Gray变换,g(u)称为u的Gray码。其中运算“⊕”为模2加法。

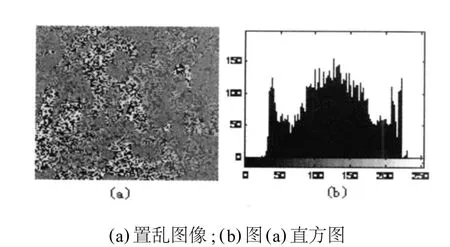
图4 基于混沌映射的置乱效果图及其直方图对比

下面给出u=0,1,2,…,15相对应的Gray码,如表2所示。

为了对Gray码进行推广和计算基于 Gray码的数字图像置乱变换的周期,下面引入广义 Gray码的概念[8]。

定义4 对于非负整数u,其q进制码记为u= (upup-1…u1u0)q,定义如下变换

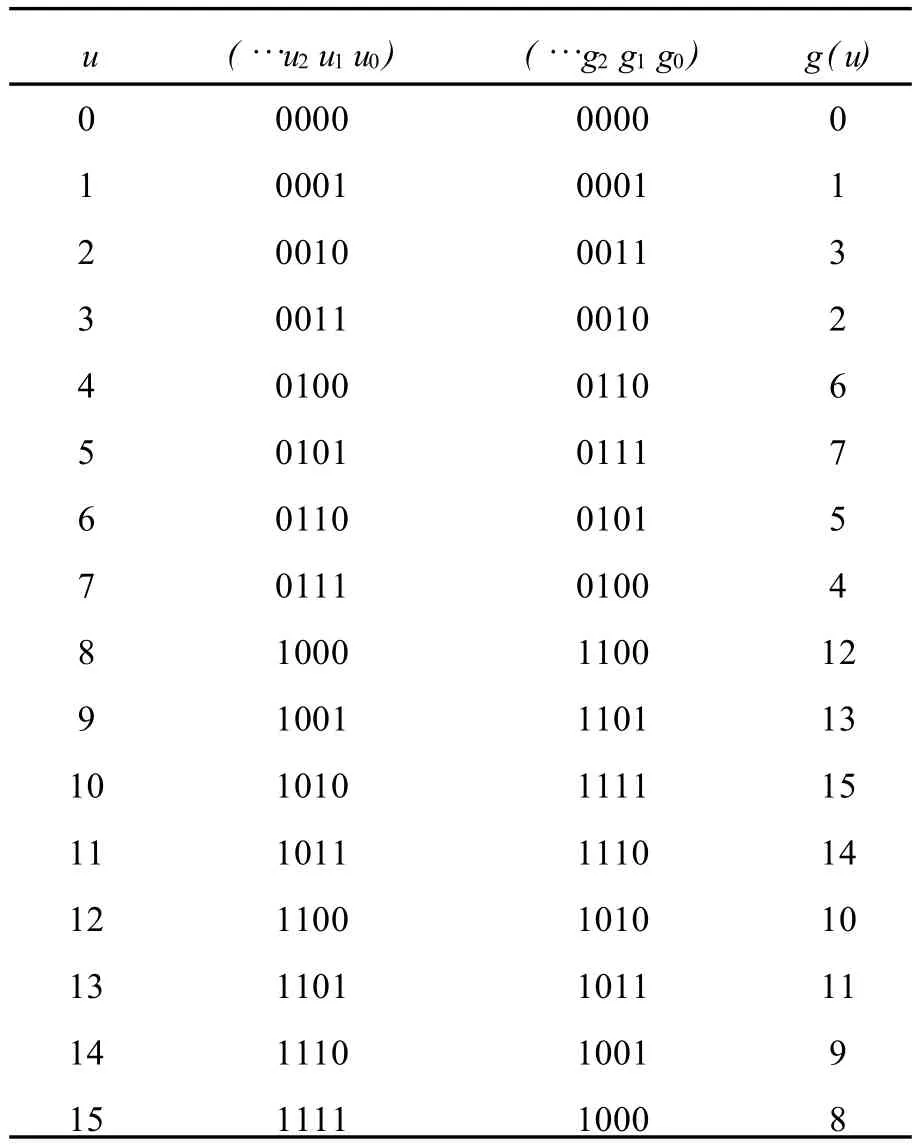
表2 u=0,1,…,15时Gray码对应表

其中,q≥2为正整数,aij为整数,i,j=0,1,…,p。当系数矩阵的行列式|(aij)|与q互素时,以上变换称为 u的广义 Gray 变换,g(u)= (gpgp-1…g1g0)q称为u的广义 Gray码。

令q=2,变换矩阵为

则式(7)为一般的 Gray变换,g(u)即为一般的Gray码。

如果式(6)中的变换矩阵仍然为以上的A,则式(4)称为 q进制 Gray变换,g(u)即为 q进制Gray码。

将三进制Gray码变换用于图像置乱方面是非常灵活的,可在位置上将一幅图像按一定的顺序对像素编号,从而利用三进制 Gray码变换重新排序置乱图像,当然也可保持位置不变,对图像的灰度值用三进制表示,再利用三进制Gray码变换,从而置乱图像。

为了得到更好的置乱效果,有些学者将基于位置空间的图像置乱方法和基于色彩的图像置乱方法相结合,即先在位置或色彩空间初步置乱图像,在得到初步置乱图像的基础上,再在色彩或位置空间进行进一步的置乱变换。显然,在经过多次置乱后,图像的置乱效果会更优,置乱周期也更长,安全性也相应的更高。

4 小结

本文深入分析了几种现有置乱方法的原理,并对其中部分置乱变换进行了仿真,通过分析实验结果得知:

1 )基于位置空间的图像置乱利用某种变换将一幅图像各像素的秩序打乱,但像素的总数及灰度值不变,可反映一幅图像的亮度信息直方图不变,这就使得该类方法存在无法改进的缺陷,如用穷举法重排置乱图像即可恢复原图像,安全性不高。

2 )在色彩空间对图像进行置乱,通过数据变换或编码技术等改变了图像的灰度值,置乱后图像直方图发生改变,与位置空间的置乱相比安全性增强。

3 )在研究这两类置乱算法的基础上,也有学者将两者结合起来用于图像置乱,也取得了较好的置乱效果。

综上,在图像的色彩空间置乱图像较之基于位置空间的图像置乱的方法,效果更优,安全性也更高,故下一步的工作重点是探索基于色彩空间的图像置乱新方法。

[1]朱桂斌.数字图像信息隐藏的理论与算法研究[D].重庆大学,2004:34-35.

[2]田云凯,贾传荧,王庆武.基于A rnold变换的图像置乱及其恢复[J].大连海事大学学报,2006,32(4):107-109.

[3]张俊萍,谭月辉.A rnold变换的置乱恢复研究[J].军械工程学院学报,2006,18(4):52-54.

[4]丁玮,闫伟齐.基于A rnold变换的数字图像置乱技术[J].计算机辅助设计与图形学学报,2001,13(4):338-341.

[5]王秀丽,宁正元.基于奇幻方的数字图像加密算法[J].闽江学院学报,2006,27(2):57-59.

[6]林雪辉,蔡利栋.基于 Hilbert曲线的数学图像置乱方法研究[J].中国体视学与图像分析,2004,9(4):224-227.

[7]李敏,费耀平.基于队列变换的数字图像置乱算法[J].计算机工程,2002,31(1):148-149,152.

[8]邹建成,李国富,齐东旭.广义 Gray码及其在数字图像置乱中的应用[J].高校应用数学学报:A辑,2002,17 (3):363-370.

[9]眭新光,罗慧.基于S盒的数字图像置乱技术[J].中国图像图形学报,2004,9(10):1223-1227.

[10]刘向东,焉德军.基于排序变换的混沌图像置乱算法[J].中国图像图形学报,2005,10(5):656-660.

[11]李国富.正交拉丁变换的周期性及其在数字图像置乱中的应用[M]//全国第三届信息隐藏学术研讨会论文集.西安:西安电子科技大学出版社,2001:1-7.

[12]Creusere C D,M itra S K.Efficient image scrambling using polyphase filter banks[M]//Proceedings of International Conference On Image Processing.USA: Austin,Texas,1994:81-85.

[13]方子毅,童卫青.基于混沌映射的图像置乱算法[J].图形图像,2007(10):51-53.