货币冲击、房地产收益波动与最优货币政策选择

陈鹄飞,陈鸿飞,郑 琦

(1.上海财经大学 金融学院,上海 200433；2.广发证券股份有限公司,广东 广州 510600；3.上海财经大学 会计学院,上海200433)

一、引 言

2008年肇始于美国房地产市场泡沫的金融危机涤荡全球。为了抵御危机,维护经济金融稳定,各国央行短时期内通过大力注入市场流动性以刺激经济增长。在宽松的货币政策下,中国房地产市场也于2007年至2009年间经历了先降后升的快速上扬行情,这对央行货币政策的调控带来了严峻的考验。回首央行近年来历次加息的房地产调控政策(2004年10月28日,2005年7月21日,2006年4月27日),我们发现这些政策非但没有立即拉低房价,反而在市场上出现了当期上涨的异象。房地产市场能否走出边调控边上涨的怪圈？货币冲击究竟对房地产投资存在怎样的传导机制？央行又是否应将房地产价格的波动纳入货币政策目标操作体系,以通过政策的锚定效应来合理引导需求预期,从而实现长期稳定的房价金融支持机制。要解答这些问题,就必须先测度出真实的货币政策冲击,并基于这种真实的货币冲击,明确计量出房地产市场预期的投资收益的波动演变路径,从而为央行实施关注资产价格波动的政策操作目标,形成合理的房地产价格调控机制,确保金融、经济的稳定和持续发展提供理论基础。

二、文献回顾

(一)国外相关研究

1.货币冲击的研究。Christiano等(1996)将VAR模型中分离出来的正交新息作为货币冲击的代理变量。但正如Rigobon和Sack(2003,2004)所指出的,由于货币政策本身存在内生性,这种冲击测算不可避免地存在内生偏误。为准确测算货币冲击,许多文献基于日内高频交易数据采用事件研究法进行分析(Ehrmaann和Fratzscher,2004)。但由于无法完全确定已发生事件的时间窗口长度,因此仍很难完全区分预期和非预期的影响。

2.房地产投资收益波动研究。Dolde和Tirtiroglu(1997)利用GARCH模型研究了房地产价格的波动,发现美国旧金山的房地产市场存在波动时变性。Wong等(2006)研究了美国和中国香港的房地产市场,证实房地产投资收益具有波动时变性。Guirguis等(2007)的研究则发现西班牙的房地产投资收益具有波动聚集性。

3.资产价格波动和最优货币政策选择。Bullard和Mitra(2002,2007)等认为货币政策不应该关注资产价格的波动,因为若货币政策对资产价格变动做出反应很可能会产生政策的不可确定性。与此相反,Kontonikas和Motagnoli(2006)则认为中央银行应该将资产价格错配纳入到扩展的利率规则之中,以对资产价格过度波动做出积极的反应。Bask(2009)的研究表明,当经济中的代理人采用最小二乘的预期方式时政策具有可确定性,中央银行应该将资产价格的错配纳入货币政策目标体系。

(二)国内相关研究

由于缺乏远期利率,目前国内主要采用VAR和SVAR的方法,将分离出来的正交新息作为货币冲击的代理变量,或者直接采用存、贷款基准利率和法定存款准备金率的变动测度货币冲击。因未能剔除市场预期,因而计量结果可能存在一定的偏误。在房地产投资收益波动的研究上,学者多采用截面数据分析,如盛松成(2003)、盛松成和刘彬(2007)通过国际比较研究了房地产价格的变动因素及货币政策的调控作用；梁云芳、高铁梅(2007)基于误差修正形式的面板数据模型研究了实际利率对房价波动的短期影响。这些研究都较少考虑房地产投资收益的波动聚集性和时变性等特征,且大多未能剔除市场预期的影响。在资产价格波动与货币政策规则的研究上,赵进文、高辉(2009)认为货币政策应将资产价格波动纳入前瞻性利率规则之中。但既有的研究较少考虑市场预期的影响,也鲜有从参与人的行为定价模式出发,研究资产价格波动与最优货币政策的选择问题,本文将以此为视角展开分析。本文的结构安排为:第三部分利用中国数据测度货币政策冲击,并估计我国房地产市场投资收益的波动方程；第四部分基于波动长记忆和参与人后向预期的行为定价动态模型,研究资产价格波动下的最优货币政策选择；最后是结论和建议。

三、货币冲击与房地产收益波动

(一)货币冲击的识别和测度

货币冲击的识别困难主要在于货币政策并非完全外生,中央银行会依据金融市场的变更和公众的需求来制订和调整货币政策。国内众多学者的研究均表明货币量在现代金融体系中是内生变量,我国的货币政策操作具有较强的内生性(万解秋、徐涛,2001)。由于迄今为止我国还没有开展远期利率协议,因此不能直接参照国外研究采用远期利率的变更来测算货币冲击。为解决这个问题,目前国内主要采用VAR和SVAR的正交新息进行研究。然而这种方法存在一个无法回避的问题,即从SVAR分离出来的货币冲击很可能不是完全外生的,政策操作的内生性导致这种冲击测算存在着内生偏误(Rigobon和Sack,2004)。基于货币政策的内生性,我们将利用泰勒规则的利率缺口,在剔除市场预期因素之后,准确测度中国市场的货币政策冲击。自从泰勒(Taylor,1993)用利率规则拟合了美联储的货币政策以来,这一规则实际上成了美联储、欧洲中央银行和英格兰银行操作货币政策的理论依据(Issing等,2001)。在我国,谢平、罗雄(2002)的研究表明泰勒规则能够为中国货币政策提供一个参照尺度。卞志村(2006)采用GMM方法估计了中国规则反应系数,结果表明通货缺口和产出缺口的反应系数分别为 0.4151和0.4958,产出缺口的反应系数与传统的泰勒规则非常一致。

盛松成、吴培新(2008)的研究表明,1998年中国人民银行宣布取消信贷规模限额直接控制后,宏观货币政策调控实体经济由直接方式向间接方式转变。同年中国住房制度改革启动,商品房体系完全按照市场经济规律由市场供求关系调节。参照卞志村(2006)估计值,我们选取季度数据,采用校准(calibrated)的货币规则公式:i*i=i*+πt+0.4151(πt-π*)+0.4958~y t,测算出中国的利率规则值i*t。样本区间为1998年1季度至2009年3季度,主要数据源于wind金融数据库。参照谢平、罗雄(2002)的研究,长期均衡真实利率i*取值为3%,目标通货膨胀率π*为4%。由于消费者价格指数CPI全面地反映了物价水平的变动,我们选用CPI衡量通货膨胀率,通过对《中国人民银行统计季报》公布的月度CPI数据移动平均得到季度CPI,通货膨胀率πt=(季度CPI-1)×100%。依照赵进文、高辉(2009)的研究,对季度GDP剔除通货膨胀算出真实GDP的对数值,再采用HP滤波计算产出缺口~y。这样就可以用实际的银行间7天同业拆借利率的季度移动平均值与规则利率的缺口it-来度量货币政策冲击。参照已有的研究(Konrad,2009),基于有效/弱有效性市场假说可知,市场无法依据历史信息预测剔除预期之后的货币冲击it-i*t。滞后4阶的货币冲击方程为:

货币冲击外生性检验的沃德检验(Wald test)值为0.76,相应的p值为0.5552。这表明原假设 H0:β1=β2=β3=β4=0不应被拒绝,利用利率缺口it-i*t度量的货币冲击具有外生性,从而避免识别货币冲击时可能存在的内生偏误。

(二)房地产投资收益的波动路径

在测度出真实的货币冲击之后,要计量货币政策对房地产市场的调控效果,还必须测算出房地产投资回报的波动演变方程。选取中经网房地产销售价格指数进行研究,由于中经网房地产销售价格指数是月度数据,我们通过移动平均得到季度数据,取对数差分得到投资回报dlogHOUPt(同比/环比价格指数对对数差分的影响差异不大)。样本区间为1998年1季度至2009年3季度,主要数据源于wind金融数据库。

1.描述性统计及GARCH-M模型设定分析。在建立波动方程之前,我们先对dlogHOUPt进行描述性统计。具体结果如表1所示。

表1 房地产市场投资收益描述性统计

表1中偏度值为负,表明季度回报具有左拖尾现象；峰度值为6.4073,凸起程度显著异于正态分布。Jarque-Bera统计值为22.7918,在1%的水平上显著异于正态分布。季度回报序列存在尖峰后尾的特征,体现出金融数据特有的分布特点。因此我们检验收益序列是否存在波动聚集性。对序列滞后一阶的自回归残差项进行拉格朗日乘子检验,统计值在1%的水平上显著,故表明收益序列存在波动聚集性,应考虑用ARCH模型进行估计。在构建ARCH模型之前,需要先对时间序列进行平稳性检验,以避免伪回归。依照赤池(Akaike,1971)的最小信息准则确定的滞后阶数为2,扩展的DF检验结果表明季度回报序列是平稳序列,可以直接建模估计。鉴于尖峰后尾和波动积聚的数据特征,依据CAPM 或ICAPM理论,风险资产的收益应当与其承担的风险成正比,风险越大预期的收益就越高,因此均值方程应包括条件方差。最小信息准则确定2阶滞后条件,由此在均值方程中加入收益序列的2阶自回归项。由于均值方程存在2阶自回归项,因而方差方程亦可能会存在跨期的条件波动聚集性,即GARCH效应,因此考虑用GARCH模型刻画这种跨期的波动聚集性。基于Engle等(1987)以及Bollerslev等(1992)对金融数据通常采用GARCH(1,1)过程建模的研究,建立利用条件方差表示预期风险的GARCH均值模型。

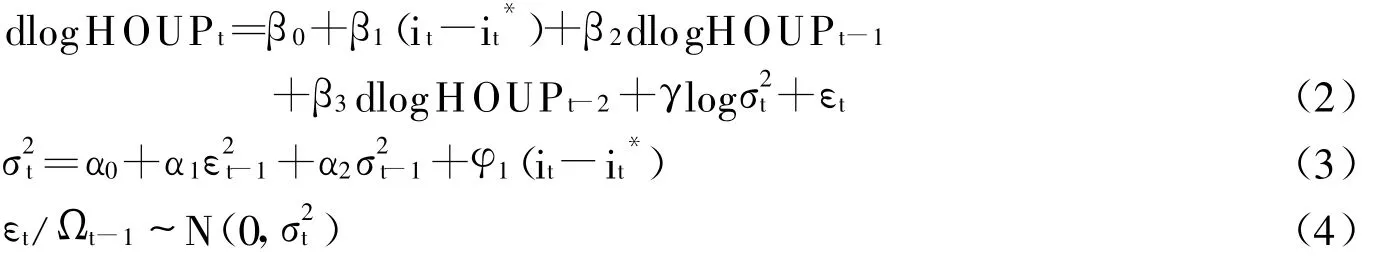
其中,dlogHOUPt为房地产销售价格指数的季度回报,依据平稳性检验时确定的滞后阶数,在均值方程中分别以dlogHOUPt-1和dlogHOUPt-2为相应的滞后一期和二期的回报序列；it-it*为货币冲击,以度量货币政策调控效果,序列的ADF检验表明其为平稳序列；价格指数季度回报的波动率以条件方差表示,用于刻画CAPM或ICAPM所预期的收益与波动的权衡关系。在波动方程中用滞后一期的残差平方项-1描述波动积聚的ARCH效应,刻画波动率的短记忆性；自回归方差项反映GARCH效应,与残差平方项一起度量波动率的长记忆效应。β0,β1,β2,β3,γ为待估参数。波动的持续性由α1+α2决定,误差项εt服从均值为0、条件方差为的分布。

2.房地产投资收益波动的GARCH(1,1)-M模型。基于描述性统计和设定分析,建立GARCH(1,1)-M度量房地产投资收益波动的演变路径。

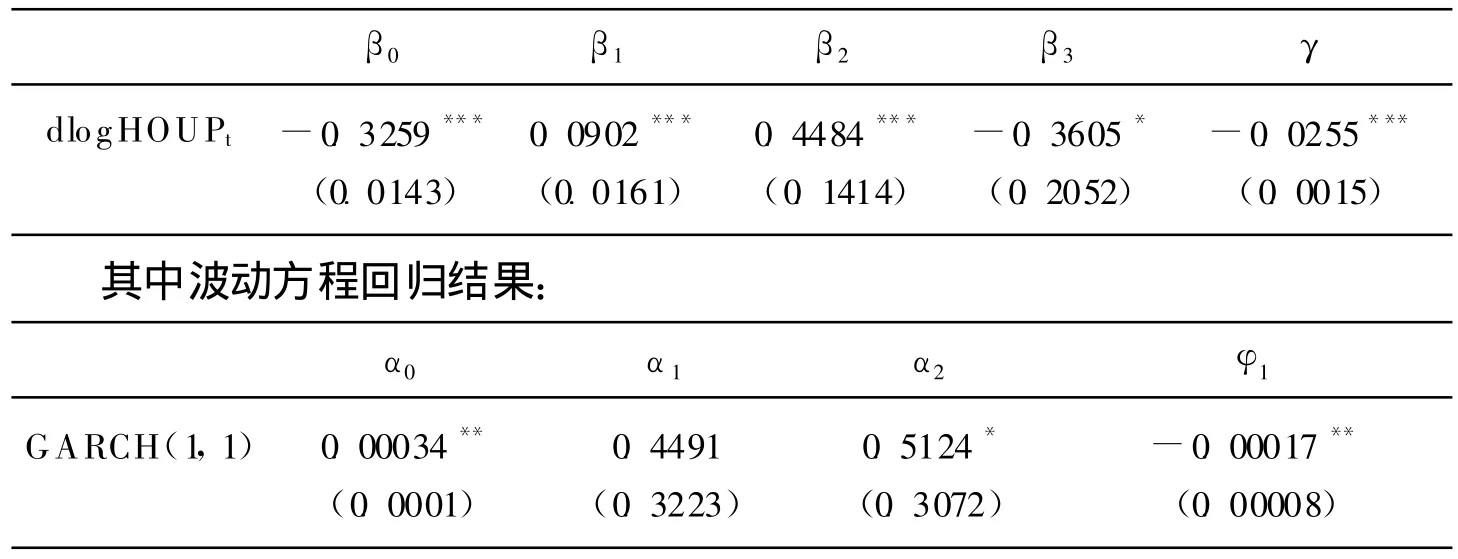
表2 房地产投资收益波动的GARCH(1,1)-M经验分析结果

先对GARCH(1,1)-M模型进行稳定性分析。依据Bollersler等(1986)的研究,GARCH族模型应满足非负性、无条件方差平稳性和GARCH平稳性条件。由表2可知,波动方程的回归系数全部为正,满足非负条件。回归的无条件方差V(εt)＞0,且波动的持续性α1+α2=0.961531＜1,满足GARCH平稳性。回归中各主要系数都显著异于0,整体拟合较好。为识别GARCHM是否捕捉波动的积聚性,经检验残差后发现残差呈不规则变动(见图1)。

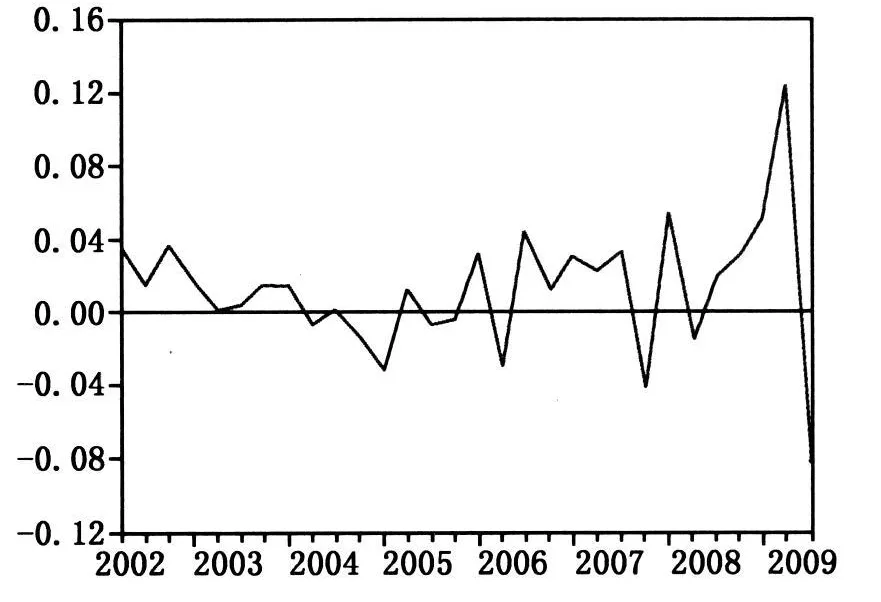
图1 残差拟合

对回归方程滞后4阶的残差序列进行ARCH-LM 检验,无论是F统计量还是残差平方自回归的可决系数给出的统计量,都表明残差不再有 ARCH 效 应,说 明GARCH(1,1)-M成功地刻画了房地产市场投资收益的波动演变路径。

(三)货币冲击与房地产市场投资收益波动的关系

首先,从表2均值方程中我们发现:货币冲击的回归系数β1至少在1%的水平上显著为正,而在波动方程中货币冲击的回归系数φ1则至少在5%的水平上显著为负。这表明实行提高利率的紧缩性政策,在同期反而会减少房地产投资收益的波动、带来投资收益的上涨。①其原因何在？我们认为还需进一步研究波动方程的回归结果,以厘清房地产市场独特的收益与风险之间的关系。

其次,从表2的波动方程我们发现:在我国的房地产投资市场上存在投资异象,投资收益与波动项的回归系数γ至少在1%的水平上显著为负。这似乎与模型设定不符,因为我们正是考虑到跨期资本资产定价(ICAPM)才采用GARCH-M建模的。而依据CAPM和Merton(1973)跨期资本资产定价模型,预期的投资回报应该与市场的风险波动正相关,高风险应该获得高的平均回报作为溢价补偿(正γ)。但是实际上均值方程的波动项回归系数(负γ)表明,在中国房地产市场上不存在投资收益与风险的跨期权衡。那么房地产投资收益的波动率又存在怎样的跨期关系呢？如果波动存在跨期时变关系,那么这种时变关系只是短期现象还是具有长记忆性呢？为此,采用两个沃德检验以研究波动项的跨期关系(见表3)。

表3 波动率跨期关系的Wald检验

波动率跨期关系检验的原假设H0:α1=α2=0,表示不存在跨期关系。由表3可见,F值和卡方值都至少在1%的水平上显著拒绝原假设,即波动存在跨期时变关系。接下来检验这种时变波动是否具有长记忆性。H0:γ=α2=0,表示没有收益与风险的跨期权衡,且波动不具有长记忆特征。F值和卡方值也都表明至少在1%的水平上显著拒绝原假设,又α1+α2=0.961531≈1,说明收益波动存在持续的长记忆性,即我国房地产市场不存在风险与收益的跨期权衡且波动具有长记忆性,这种独特的风险与收益的计量关系直接催生了市场的投资异象,其外在表现就是媒体所报道的房价边调边涨的怪圈。那么这种投资异象存在怎样的理论和现实基础呢？

最后,我们结合学界已有的研究和中国房地产业的现实特征对这一异象予以阐释。Abel(1988)以及Gennotte和Marsh(1993)的资产组合配置观为理解房地产市场的投资异象提供了合理的解释。基于全部资产组合配置的考虑,投资者可能愿意放弃部分资产的投资溢价补偿,尤其是在通胀预期压力持续加大的情况下,由于缺乏合理的投资渠道和相应的通胀指数国债来对冲投资的通货膨胀风险,因此,投资者出于整体资产配置的考虑,投资不动产时愿意放弃获取补偿溢价,从而形成收益与风险的负相关。Bekaert和Wu(2000)、Bae等(2007)等则从杠杆效应(financial leverage)的角度就投资异象予以了解释。他们认为金融投资大都采用信贷驱动的高杠杆操作模式,由于市场投资回报的增加,相对降低了投资杠杆比率,因而愿意放弃高的补偿溢价。在当前既定的产业结构下,服务于稳定增长的大局,中央银行的货币、信贷政策总是在短期救急和长期发展之间不断进行平衡。类似于“格林斯潘卖权”,政策效应极大地提高了投资的杠杆率,财富效应刺激了投资性需求的不断高涨,从而进一步推升了房价。只要加息不足以刺破金融泡沫,信贷投资的杠杆效应足以补偿风险溢价,就会出现投资异象,导致房价边调边涨。另外,由于缺乏明确的资产价格锚定预期,市场基于以往房价上涨趋势采用后向定价的惯性投资策略,从波动的持续性来看,α1+α2高达0.961531,说明市场对于货币政策调控新息的反应极为有限,市场投机氛围浓郁。

四、最优货币政策选择

鉴于房地产行业的财富效应和投资拉动作用,综合市场参与者的后向预期和波动长记忆性特征,建立行为资产定价的动态模型,研究最优货币政策的选择,为中央银行实施关注房地产价格波动的政策提供理论依据。

(一)动态模型的构建

肖争艳、陈彦斌(2004)的研究表明,决定我国实际通货膨胀率变动的主要因素是滞后一期的实际通货膨胀率。基于他们的研究结果以及房地产业的财富效应,借鉴Bask(2009)等人的研究,构建标准的动态模型:

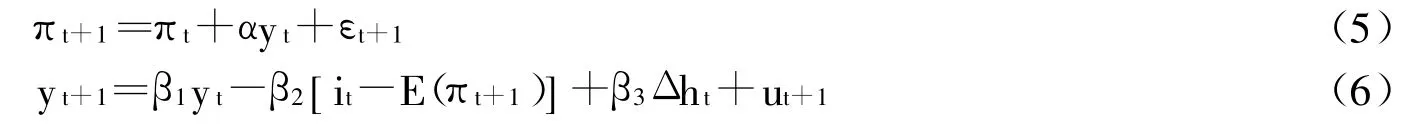
其中,yt依通常设定,代表对数线性化后与产出“稳态”的偏离值,πt为通货膨胀率(确切地说,应是与目标通胀的偏离值),it为名义利率,ht代表取对数值形式后的实际地产价格(如房地产销售价格指数),假定随机波动序列εt+1、ut+1满足独立同分布。与肖争艳、陈彦斌(2004)的研究相一致,我们设定标准的后向定价的新凯恩斯菲利普斯方程(5),用以刻画实际通货膨胀率的变动主要是由滞后一期的实际通货膨胀率的变动所决定。考虑我国房地产业的财富效应,在标准的需求方程中加入β3Δht,其中β3反映房价变动所带来的财富效应值,当β3=0时(6)式即为传统的动态IS方程。基于市场参与者的后向预期特点和波动长记忆性特征,建立房地产价格的行为资产定价方程。参照Kontonikas和Montagnoli(2006)研究,认为基本面投资者预期的价格由以下的股息定价模型决定-Et[pt+1]=ζEt[y t+1]-η[it-Et(πt+1)]。其中代表基本面决定的房地产名义价格指数,p为物价水平,预期折现股息流与未来的产出缺口正相关,与紧缩性货币政策负相关。基本房价指数为:

由于存在波动长记忆性,我们假定趋势交易者依如下定价方式来预期房地产价格=θΔht-1,其中θ代表波动记忆性,波动的记忆性越强则过去房价的发展对当期房价的影响越大,即:Δht=+(1-w),其中w代表趋势投机者的比重,故房地产市场行为资产定价方程为:

投机者越多(w变大),波动的记忆性越长(θ变大),房价就越非理性变动,调控作用也就越弱。通过先将(8)式代入(6)式,再将(5)式回代,并基于t期取期望值得,得到集约表达形式

(二)最优货币政策的选择

假定中央银行为实现社会福利最优,采用跨期二次型目标损失函数:

其中,λ≥0为中央银行的产出缺口权重,跨期折现因子0＜τ＜1,在第t期央行自主决定利率,而由φt可知,此时可以得到如下的值函数:

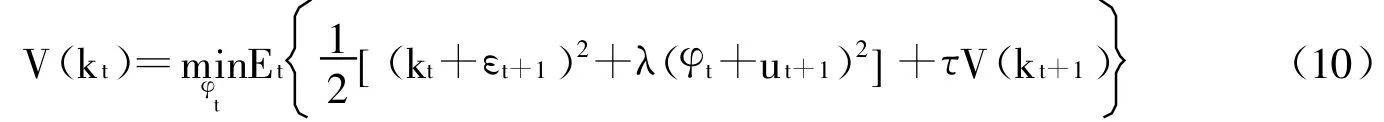
依据包络定理和一阶优化条件,我们求得控制变量的如下闭型解:

即货币政策取决于一国的通货膨胀、经济增长和房地产价格波动状况。②

命题:当房地产业具有巨大的财富效应,或当其市场参与者具有持续的波动长记忆性时,货币当局应关注房地产资产价格波动,以发挥政策的锚定效应。

证明:由动态模型的设定可知,房地产业的投资拉动作用和财富效应主要由动态IS方程β3度量,市场参与者的波动长记忆性则由资产定价方程中的θ刻画。将最优解对β3和θ求偏导数,由于经济中的外生参数都为正数,得:

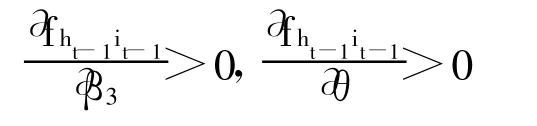
即货币当局应该明确关注房地产价格的波动,发挥货币政策的价格锚定效应。事实上,反观以往决策层的调控措施,由于缺乏政策的连续性和稳定性,自从2004年以来的国八条、国六条陆续出台,房价没有随着调控下降,反而是不断上涨。同时,央行并没有将房地产价格变动明确纳入调控目标,在房价不断上涨的背景下,居民资产价格预期缺乏锚定效应,投资者依据以往信息实行后向定价,整个市场对于货币调控的反应极为有限。因此,基于当前房地产的产业特点和经济增长模式,央行明确实施关注资产价格波动的操作目标,充分发挥货币政策的资产价格预期锚定效应,对合理引导需求预期、有效地分层次调控市场需求以及实现长期稳定的房价形成机制具有重要意义。

五、结论和建议

在利用利率缺口测度货币冲击后,本文基于GARCH(1,1)-M模型度量了我国房地产市场投资收益波动的演变路径,解析了房地产市场存在的投资异象和波动长记忆性特征。并基于房地产业的财富效应和市场投资者的后向定价特征,构建了包含行为资产定价的动态模型,研究了资产价格波动下的最优货币政策选择,明确货币当局应该实施关注资产价格波动的目标操作体系,以发挥货币政策的价格预期锚定效应,合理引导需求预期,有效分层次调控市场需求。当然,为使房地产市场向健康、良性的方向发展,还必须适当采取综合调控手段,调控政策要在方向、重点和力度上相互协调配合,在作用期限上统筹安排。既要有短期立竿见影的政策,又要有中长期的政策储备。如果仅仅依赖中长期政策,就会“远水解不了近渴”；如果只有短期政策,就难以改变人们预期。既要向同一个方向和重点上使劲,又要防止政策叠加效应导致政策力度过大。通过区分不同政策的不同着力期限,做到统筹安排。最终通过政策之间的协调配合、统筹安排,合理引导需求预期,有效地分层次调控市场需求,以实现长期稳定的房价形成机制。

注释:

①考虑政策时滞影响,均值方程加入滞后1期的货币冲击仍然为正,滞后2期后发现虽同期冲击为负,但回归系数不显著,GARCH族稳定性无法满足,表明房地产市场可能存在波动长记忆性。

②只要经济处于合理的状况,即fπ＞1,fy＞0,此时最优货币政策就具有可操作性,证明备索。

[1]盛松成.货币政策能否调控房地产价格[J].银行家2003,(9):30-33.

[2]盛松成,刘斌.经济发展对房价长期走势的决定因素——基于中国及国际的比较分析[J].财贸经济,2007,(8):109-114.

[3]赵进文,高辉.资产价格波动对中国货币政策的影响——基于1994年到2006年季度数据的实证分析[J].中国社会科学,2009,(2):98-114.

[4]卞志村.泰勒规则的实证问题及在中国的检验[J].金融研究,2006,(8):56-69.

[5]盛松成,吴培新.中国货币政策的二元传导机制——“两中介目标,两调控对象”模式研究[J],经济研究,2008,(10):37-51.

[6]Bask B,Mikael.Monetary policy,stock price misalignments and macroeconomic instability[R].Working Paper,2009.

[7]Bullard J,Mitra K.Determinacy,learnability,and monetary policy inertia[J].Journal of Money,Credit and Banking,2007,39:1177-1212.

[8]Ehrmann M,Fratzscher M.Global financial transmission of monetary policy shocks[R].Working Paper,2006.

[9]Guirguis H,Gianniko S,Garcia G.Price and volatility spillovers between large and small cities:A study of the spanish market[J].Journal of Real Estate Portfolio Management,2007,13:311-316.

[10]Konrad,Ernst.The impact of monetary policy surprises on asset return volatility:The case of germany[J].Finance Market Portfolio Management,2009,23:111-135.