DFT频谱分析系统的FPGA设计与实现

陈至坤，李 胜，陈 韬，王福斌，孙晓磊

(1.河北理工大学计算机与自动控制学院，河北 唐山063009;2.天津市德力电子仪器有限公司，天津300113;3.东北大学机械工程与自动化学院，辽宁 沈阳110004;4.天津大学电信学院，天津300072)

0 引言

有限长序列离散傅里叶变换(discrete Fourier transform，DFT)和快速傅里叶变换(FFT)是数字信号频谱分析的基本算法。一般来说，FFT算法由于利用了DFT的一些固有特性，减少了DFT运算量，是计算信号频谱的常用方法，但是在某些实际应用场合，应用DFT完成系统设计与FFT相比更有优势［1］。数字信号处理系统过去常采用高速的ASIC器件来实现。然而，随着半导体器件技术的发展，这些专用器件已经逐渐由现场可编程(逻辑)门阵列(field programmable gate arrays，FPGA)代替。FPGA具有高速度、高集成度和高可靠性，而且具有用户可编程特性，能降低设计风险。基于FPGA的DFT频谱分析系统，

可以用硬件实现软件算法，大大提高了运算速度，解决了DFT运算量大、消耗时间长、实时性不好等实际应用的问题。另外，在用FPGA计算频谱时，速度已不是频谱计算的瓶颈，更重要的是资源的合理应用［2］。本文将详细介绍DFT频谱分析算法的FPGA设计与实现。

1 DFT频谱分析系统总体设计

DFT频谱分析算法的数学公式为

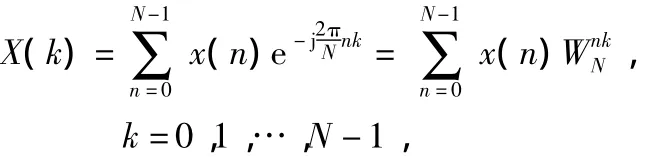
式中 x(n)为时域信号，X(k)为频域信号。根据DFT算法的数学公式，DFT频谱分析系统总体设计如图1所示。系统以二分频高速A/D的转换频率为时钟。经过高速A/D转换后的数字化实信号，先由双端口RAM采集。然后，在时钟的控制作用下，依次进行数据加窗、数字下变频、累加、平方、求和、开方运算，最终将处理结果存储。图1所示所有的工作全部在FPGA中完成。同时，整个频谱分析系统需要外部MCU(单片机或DSP)发送重置、开始、停止等控制命令字并对处理完成的数据进一步传输和显示。

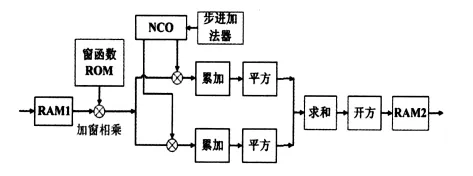
图1 系统总体框图Fig 1 Overall block diagram of the system

2 主要功能模块的设计

2.1 信号采集存储模块

数字信号采集存储模块的设计，既要求能准确采集所需点数的数据，同时也要为后续数据处理做准备。双口RAM具有两套完全独立的数据线、地址线和读写控制线，并允许2个独立的系统同时对该存储器进行随机性的访问。使用双端口RAM提高了RAM的吞吐率，不会造成大数据量情况下数据堵塞的现象，适用于实时的数据缓存。设计中采用了双端口RAM作为信号采集存储模块。图2所示为双端口RAM的逻辑结构图。

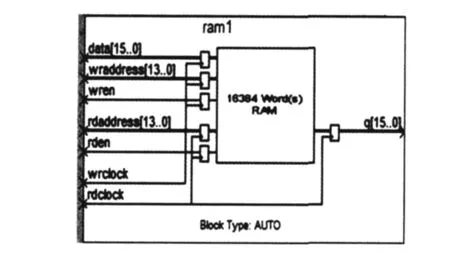
图2 双端口RAM逻辑结构Fig 2 Logic structure of dual-port RAM

在图2中，data为A/D输入数据;wraddress为14位宽写入端的地址，可以寻址16384个单元，满足每一次操作存储采样数据的要求;wren为写入端的写使能信号;inclock为写入端的时钟，因为设计采用是时序电路，所以，电路中的任何动作都要在时钟的驱动下进行。q，rdaddress，rden，outclock分别为双口RAM读出端数据线，地址线，读使能以及该端的时钟。数据的写入时钟是A/D的转换时钟166.4 MHz，后续系统的读取时钟为83.2 MHz。读取时钟远比写入的速度慢，保证了数据的准确性和稳定性。

2.2 窗函数选择与存储模块

由于矩形窗对信号进行截取会造成“频谱泄漏”，所以，需要改用其他窗函数对信号进行截取。常用的窗函数有汉宁窗、海明窗、布莱克曼窗、布莱克曼—哈里斯窗等，通过对几个窗函数参数的比较，设计中选用布莱克曼窗作为窗函数。由于各个窗函数的频谱是不同的，所以，同样的RBW在不同的窗函数下对应的处理数据点数也是不同的。一个N点正弦采样信号

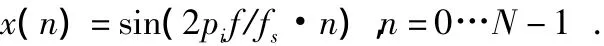
其DTFT模的波形在分贝图上看，3dB处宽度对应着的模拟的频率就应该为RBW。有限长度正弦数字信号加上布莱克曼窗后的取分贝的频谱图如图3所示，从图中可以看出:3 dB带宽对应的角频率差为1.65×2π/N，对应的模拟频率为1.65 fs/N，所以，需要采样数据点数N=1.65fs/RBW。

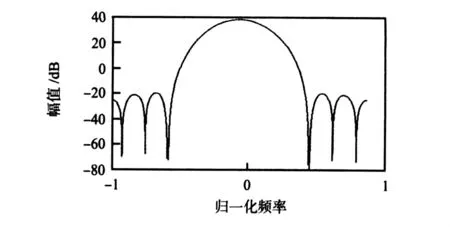
图3 有限长正弦数字信号加布莱克曼窗后取分贝的频谱图Fig 3 Spectrum of finite sinusoidal digital signal multiply Blackman window

通过Matlab软件，生成所需点数窗的值，存入FPGA创建的ROM模块之中，按照时钟的时序将ROM中存储的窗函数值依次与A/D转换后的数据相乘，从而实现数据加窗的操作过程。因为窗函数具有对称性，所以，在设计中只需要存入对称的一半窗函数的值即可，这样可以减少存储器资源，节约硬件成本。

2.3 NCO IP Core模块

为了缩短开发设计周期，减少设计风险和资金投入，同时提高性能和可靠性，本设计采用Altera公司NCO模块IP核实现数字下变频［3］。

IP核(intellectual property core)是FPGA厂商和第三方预先设计好各种通用单元并根据各种FPGA芯片的结构对布局和布线进行优化，从而构成具有自主知识产权的功能模块。IP核具有重用性，适用于不同的系统。IP模块可分为硬件(Hard IP)模块、软件(Soft IP)模块和固件(Firm IP)模块 3 种［4］。

在本设计中数控振荡器(numerically controlled oscillator，NCO)用来产生频率可变的正余弦样本。NCO V 7.2是Altera公司2007年发布的 NCO IP core，支持该公司的Cyclone，Stratix等系列FPGA器件。该NCOIPcore提供Small ROM，Large Rom，CORDIC，Multiplier-Based 4种结构的 NCO设计。本设计采用CORDIC算法实现。采用CORDIC算法实时计算正余弦样本，避免了采用Small ROM，Large Rom查找表结构耗费大量ROM资源和使用Multiplier-Based乘法器结构需要DSP模块，对FPGA的要求高的缺点［5］。

在QuartusII 7.2中，选择 tools-＞Mega Wizard Plug-In Manager，然后，选择 DSP-＞Signal Generation-＞NCO V 7.2创建NCO模块。NCO模块逻辑结构如图4所示。

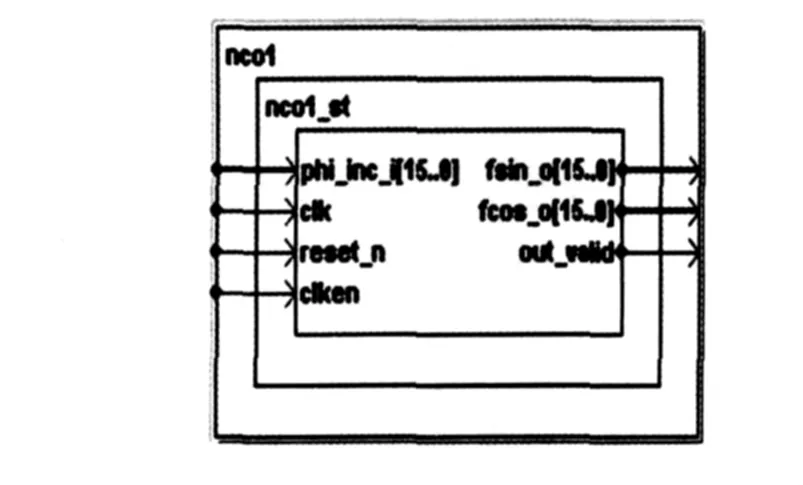
图4 NCO模块逻辑结构图Fig 4 Logic structure diagram of NCO module

NCO模块共有4个输入量，分别为时钟信号，时钟使能，相位增量和复位。在对时钟信号，时钟使能，相位增量设置完初值后，当复位信号由低置为高后，NCO产生相应的正弦和余弦输出。

3 NCO模块对系统的精度影响分析

NCO能否准确地产生所需频率正交的正弦和余弦样本，将会影响频谱分析系统的精度。

影响数字下变频性能的主要因素有2个:一是表示数字本振、输入信号以及混频乘法运算的样本数值的有限字长所引起的误差;二是数字本振相位的分辨率不够而引起数字本振样本数值的近似取值。也就是说，如果数字混频器和数字本振的数据位数不够宽，就存在着尾数截断的情况，数字本振相位的样本值存在近似的情况，则根据截断和近似的程度，会或多或少地影响NCO的性能［7］。

设计中每计算一个频域点值，就需要相应频率的正余弦样本，因为相邻频域点值的频率差值是固定的，所以，生成的正余弦样本值的频率差值也是固定的，设计中在NCO模块输入前加入一个加法器，加法器的2个加数分别称起始值和步长值，初值由第1个频点值确定，步长值由相邻频点的频率差值确定。步长值和初值数值的确定参照NCO IP core说明文档中具体公式。图5所示为NCO模块前的加法器模块。

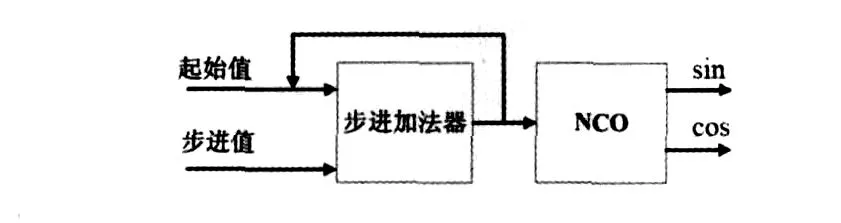
图5 NCO模块输入部分结构图Fig 5 Input part structure diagram of NCO module

实验中发现，当NCO输入精度为16位，有步进值加入时，输出正余弦样本的频率并没有发生变化，仍然保持未加步进时的值。当NCO输入精度为32位，有步进值加入时，输出正余弦样本能够比较准确地输出相应的频率。因此，正余弦样本能否正确的产生取决于NCO模块输入的数字本振相位的分辨率精度。NCO模块输入数字本振相位的分辨率精度不够的时候，输入值有较小变化的时候，输出不变，从而造成输出正余弦样本不准确。图6所示为NCO在16位精度输入在200 kHz的span下的频谱图，从图中可以看到频谱图有明显的“阶梯状”。图7所示为NCO在32位精度输入在200kHz下的频谱图。在32位精度输入下信号频谱更加精细。

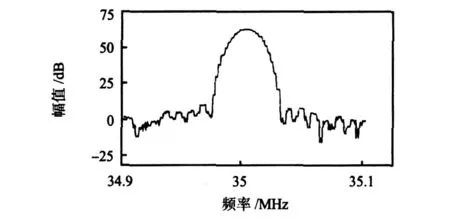
图6 16位精度输入200 k Hz span频谱分析结果图Fig 6 Spectrum analysis result diagram of 16-bit precision input with 200 kHz span

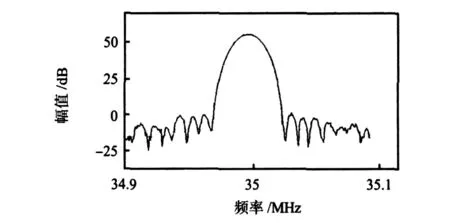
图7 32位精度输入200 k Hz span频谱分析结果图Fig 7 Spectrum analysis result diagram of 32-bit precision input with 200 kHz span

4 DFT频谱分析系统的实现与性能分析

本设计采用Altera公司的Cyclone III系列的EP3C25E144C8芯片，在QuartusII 7.2版本开发平台上实现。Cyclone III是Altera公司2007年生产的系列器件，采用了交叉I/O环，宽列低成本包装，支持低成本闪存。CycloneIII器件是低功耗的65 nm的FPGA，未使用的I/O块被置为低电平。Cyclone III增加了系统的集成度，密度高达119088个逻辑单元，存储器高达3.8 Mbits，其内部有4个锁相环，提供了强大的时钟控制，可综合器件时钟、外部时钟和I/O接口，可以支持高达400 Mbps的外部高速存储器。

在具体的实现过程中，为了加快DFT频谱分析系统的速度，采用了两条相同的DFT处理结构，并行处理，并将处理结果依次存储。从而使整个DFT处理的时间减半。实验验证过程中，在5～65MHz范围内输入35MHz单一信号，将处理完成的数据输入到DSP处理芯片中，结合Visual DSP++调试工具，得到图8所示的仿真结果。验证过程中还分别对不同中心频率，不同的span下的情况下进行了仿真，仿真结果验证了DFT频谱分析系统的正确性。

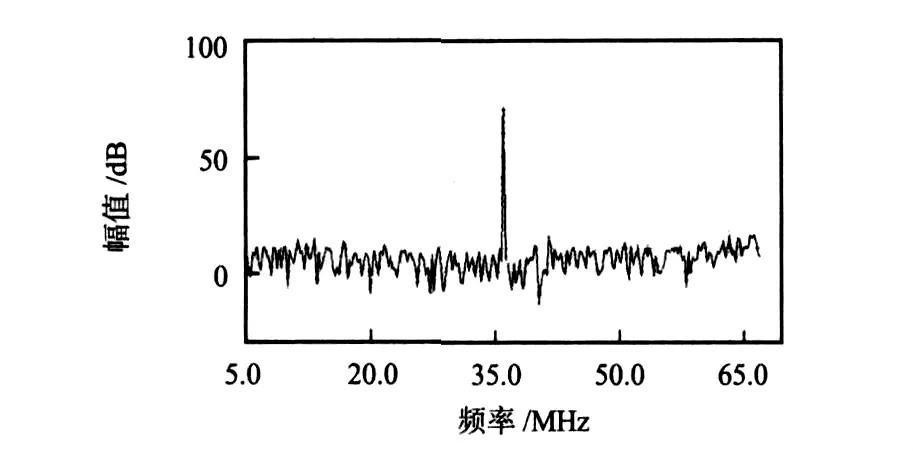
图8 32位精度输入60MHz span下35MHz信号频谱分析结果图Fig 8 35 MHz signal spectrum analysis result diagram of 32-bit precision input with 60 MHz span

表1所示为系统采样16 384数据点值，采用二路并行处理下的FPGA的资源消耗，系统工作频率为83.2MHz，每场数据处理时间为22 ms。

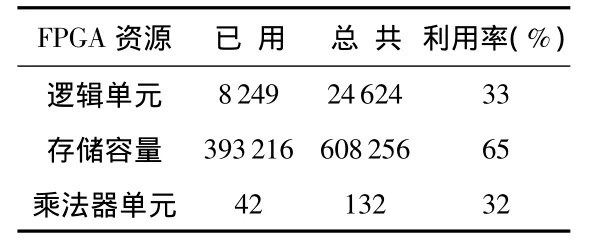
表1 并行处理结构下频谱分析系统资源消耗量Tab 1 Resource consumption of the system

在相同的条件下，采用Altera公司的FFT IP core V 7.2设计的FFT频谱分析系统，占用的存储单元容量为1060160。远远超过了选用FPGA芯片的存储容量，造成成本的增加。

5 结束语

本文设计与实现了一种适合FPGA实现的DFT频谱分析系统，本系统全部由VHDL语言实现。实验结果表明:该设计采用NCOIPcore实时计算需要的正余弦样本，能够比较合理地利用FPGA资源。对于本系统需要处理16 384采样点数据的要求，采用DFT频谱分析算法虽然比FFT算法消耗时间长，但可以节省大量的芯片资源，同时由于FPGA器件处理速度的快速性，整个系统22 ms处理一场数据满足应用要求。此外，该系统还具有功耗低、接口简单、系统外部只需要一些简单的控制信号便于移植到其他系统中去的优点，具有很强的应用价值。

［1］邱宽民，赵胜凯.DFT与FFT在实际应用时的性能比较［J］.北方交通大学学报，2000(10):60－62.

［2］陈永东.一种基于FPGA的DFT算法实现的研究［J］，遥测遥控，2005(7):53－69.

［3］刘祖深.频谱分析仪全数字中频设计研究与实现［J］，电子测量与仪器学报，2009(2):39－49.

［4］窦秀梅，赵振纲.基于IP核的FPGA FFT算法模块的设计与实现［J］.无线电工程，2008(8):29－31.

［5］陈绍宽，李 明.NCO的研究及其FPGA实现［J］.仪表技术，2006(5):30－32.

［6］NCOMega Core Function User Guide［EB/OL］.［2007—10—01］.http://www.altera.com.

［7］何水艳.浅析数字下变频中的NCO［J］.高等函授学报:自然科学版，2004(2):53－56.