基于自适应波形匹配延拓的局部均值分解端点效应处理方法

张 亢 程军圣 杨 宇

湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

0 引言

局部均值分解(local mean decomposition,LMD)是由Smith[1]提出的一种新的非线性和非平稳信号分析方法。由于LMD是依据信号本身的信息进行自适应分解的,产生的PF分量具有真实的物理意义,由此得到的时频分布能够清晰准确地反映出信号能量在空间各尺度上的分布规律,因此LMD是一种极具发展潜力的非平稳信号分析方法,现在它已在脑电信号分析中得到了应用[1],并且取得了不错的效果。

虽然LMD非常适合于处理非平稳信号,但作为一种新出现的信号分析方法,此方法本身还有一些需要改进的地方,其中端点效应就是必须解决的问题之一。如同经验模式分解(empirical mode decomposition,EMD)[2-3]一样,LMD方法中也有一个类似的依据信号局部极值点信息不断进行“筛分”信号的过程,在“筛”的过程中,需要不断地平滑由信号局部极值点构成的局部均值函数线与包络估计函数线,但由于信号两端的值可能既不是局部极大值也不是局部极小值,这样便会造成平滑过程中局部均值函数线与包络估计函数线在数据两端出现发散现象,并且这种发散的结果会逐渐向内“污染”整个数据序列而使所得的分解结果严重失真。

对于EMD方法的端点效应问题,目前已提出了许多改进方法,都取得了一定的效果,但也存在一些局限性,如极值点延拓法[4]只考虑了信号端点附近几个极值点的信息,而没有顾及信号内部的规律,因此对较复杂的非平稳信号,效果不太理想;边界波形匹配预测法[5]考虑了信号的内部规律与趋势,但缺乏自适应性,对于边缘处波形发生了突变的信号效果比较差;神经网络[6]、ARMA模型[7]等预测类延拓方法,其改进效果很大程度上依赖于预测工具本身参数的设置,同时运算时间也较长,缺乏实用性。

本文根据许多改进EMD端点效应方法的经验与不足,在详细分析了LMD端点效应产生的原因的基础上,提出了自适应波形匹配延拓方法,以解决LMD的端点效应。

1 局部均值分解方法

LMD的整体思路就是依据信号的局部时间尺度特征,将信号从高频到低频自适应地逐级分解出来,分解后的每个分量都是平稳且具有物理意义的。对于任意信号x(t),其分解过程如下[1]。

(1)找出原始信号所有的局部极值点ni,求出所有相邻的局部极值点的平均值:

将所有相邻的平均值点mi用直线连接起来,然后用滑动平均法进行平滑处理,得到局部均值函数m11(t)。

(2)求出包络估计值:

将所有相邻两个包络估计值ai用直线连接,然后采用滑动平均方法进行平滑处理,得到包络估计函数a11(t)。

(3)将局部均值函数m11(t)从原始信号x(t)中分离出来,得到

(4)用h11(t)除以包络估计函数a11(t)以对h11(t)进行解调,得到

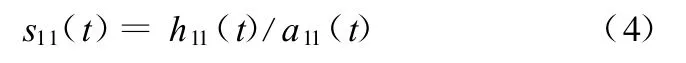
对s11(t)重复上述步骤便能得到s11(t)的包络估计函数 a12(t),假如a12(t)不等于1,说明s11(t)不是一个纯调频信号,需要重复上述迭代过程n次,直至s1n(t)为一个纯调频信号,也即s1n(t)的包络估计函数a1(n+1)(t)=1。在实际应用中,可以设定一个变动量 Δ,当满足1—Δ≤a1n(t)≤1+Δ时,迭代终止。

(5)把迭代过程中产生的所有包络估计函数相乘便可以得到包络信号(瞬时幅值函数):

(6)将包络信号a1(t)和纯调频信号s1n(t)相乘便可以得到原始信号的第一个PF分量

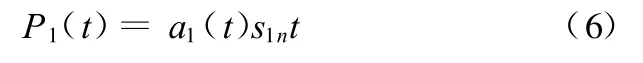
它包含了原始信号中最高的频率成分,是一个单分量的调幅—调频信号,其瞬时幅值就是包络信号a1(t),其瞬时频率 f1(t)则可由纯调频信号s1n(t)求出,即

(7)将第一个PF分量P1(t)从原始信号x(t)中分离出来,得到一个新的信号u1(t),将u1(t)作为原始数据重复以上步骤,循环k次,直到uk为一个单调函数为止:

原始信号 x(t)能够被所有的 PF分量和 uk重构,即

(8)将所有PF分量的瞬时频率与瞬时幅值按照时间—频率—幅值的三维分布重新组合,便能得到原信号基于 LMD分解的完整的时频分布。

2 LM D分解的端点效应分析

从上述LMD分解的步骤中可以看出,之所以会产生端点效应,关键是由于求取局部均值函数和包络估计函数时需要用到信号序列局部极值点的信息,其中局部均值函数是通过不断地平滑由相邻极值点的平均值构成的直线段而获得的,包络估计函数是通过不断地平滑由相邻极值点差的绝对值的一半构成的直线段而获得的,然而数据的两端点值不一定是信号的极值点,因此这样得到的局部均值曲线与包络估计曲线在数据的两端是不合理的。考察信号x(t):

其局部均值线段和包络估计线段如图1所示,而真实的局部均值线段和包络估计线段如图2所示,可以看出在数据两端其值都出现了失真,将其平滑后得到的局部均值曲线和包络估计曲线与真实的曲线比较,如图3所示,其两端的数据同样出现了失真。

由于局部均值曲线与包络估计曲线失真,便会造成分解后得到的PF分量的两端出现虚假成分,并且随着分解过程的进行,局部极值点的不断减少、稀疏,这些虚假成分会逐渐向内“污染”整个数据,最终造成分解结果的失真,即“端点效应”,数据越短,其危害性越大。为了减小(不可能完全消除)上述LMD的端点效应,本文针对其产生的原因,从信号的自然趋势与相似性着手,提出一种自适应波形匹配延拓法来改善LMD的端点效应现象。

3 自适应波形匹配延拓法

为了解决 LMD分解的端点效应问题,我们对原信号两端进行延拓,将失真尽可能地隔离在待分析信号的外部。然而这种延拓不能是盲目的延拓,而是要使延拓出的波形尽可能地符合原信号自然的变化趋势,这样才能最大限度的维护原始信号的变化趋势并实现延拓波形与原信号的光滑过渡,从而更加有效地抑制端点效应。基于以上,我们提出了自适应波形匹配延拓法,即从原始信号内部找出最符合信号趋势的波形对信号进行延拓,最大限度地维护信号的内在趋势,而对内在规律较弱,边界数据变化异常的信号可以只考虑信号边缘的极值点信息,具体通过设定一阈值来实现,这样可使该方法具有自适应性。

信号的延拓包括左右两端,下面以左端的延拓为例来说明该方法。设原始信号为 x(t),m′i、n′i(i=1,2,3,…)分别为信号x(t)的极大值和极小值,分别对应时间为和,设x(t)的左端点数据为x(1),以 x(1)—m′1—n′1三点构成一个三角波形,并将其称为特征波形,然后沿着信号 x(t)搜索与特征波形最为匹配的三角波形x(i)—m′i—n′i,定义为匹配波形,将匹配波形前的(右延拓为匹配波形后的)数据作为x(t)的延拓波形,这样便会符合信号的自然趋势。具体步骤如下。

(1)寻找出除特征波形外所有三角波形的起始点值x(i),其对应的时间点为

求出的tx(i)可能不正好在采样点上,这时可用插值法(具体插值法可由自己选定)求出其确切值。

(2)计算所有三角波形与特征波形的匹配误差,误差公式为

(3)找出最小的匹配误差值mine(i),并设定一阈值α,如果mine(i)＜α,则将mine(i)对应的三角波形作为匹配波形,将匹配波形前的数据延拓到原始信号的前面,如果mine(i)≥α,跳转至下一步。阈值的大小可根据实际情况来调整,α越小说明原信号具有越强的规律性,反之说明原信号内在规律越弱,或边界数据有较大的异常。

(4)直接设置信号端点处的极值,即分别求出最靠近信号端的相邻的N个极大值点的平均值和M个极小值点的平均值,将其分别作为信号x(t)的极大值和极小值,具体N和M的大小可根据信号在边界处的跳变情况而定。

(5)按同样的方法延拓右端的信号,设完全延拓后的信号为 x′(t)。

(6)将延拓后的信号 x′(t)做 LMD分解,对分解得到的PF分量按原信号x(t)对应的时刻进行截取,这样便能获得改善了端点效应的分解结果。

(7)将x′(t)做LMD分解后得到的瞬时幅值和瞬时频率,以原信号x(t)所对应的时刻按频率—时间—幅值分布进行组合,得到最后完整的时频图。

上述对信号进行延拓的方法,不但充分考虑了信号的内在规律与趋势,使延拓部分与原信号能光滑过渡,减小了分解结果在端点处的振荡,同时对内部规律较弱或边界数据异常的信号,也能进行较好的处理,较之通常的端点处理算法有更强的自适应性。

4 仿真信号分析

为了验证该方法的可行性,取由3个正弦波叠加的信号进行分析,该信号表达式为

信号的时域波形如图4所示,可以看出其内部规律较强,所以信号延拓时阈值α可以定得较小,本文设置α=0.1。

对采用本文方法延拓后的信号进行LMD分解,结果如图5所示,对信号x(t)直接进行LMD分解,结果如图6所示。对比可以看出,没有进行端点处理的分解结果在数据两端出现了明显的摆动,而采用本文方法延拓后得到的分解结果几乎完全消除了端点效应的影响,分解结果非常理想。

图7所示是信号x(t)的EMD分解结果,与LMD的分解结果比较,其端点效应更加严重,低频时数据发散严重,并且最低频的5Hz分量不能分解出来,产生了模态混淆现象。图8所示是信号x(t)采用本文方法延拓后进行EMD分解的结果,可以看出其端点效应得到了较大的改善,说明该方法也能较好地改善EMD的端点效应,但是5Hz分量仍然无法分解出来,存在模态混淆现象。综合比较,LMD方法在端点效应和模态混淆方面要优于EMD。

进一步将信号延拓前和延拓后进行LMD分解得到的瞬时幅值与瞬时频率分别进行组合,获得按频率—时间—幅值分布的时频分布,分别如图9、图10所示,可以看出延拓前的时频分布在端点处出现了明显的振荡现象,端点处能量发生了泄漏;而延拓后的时频分布清晰准确地反映了原信号的各个频率成分,端点处的振荡几乎消失。

在H HT变换中,除了在EMD分解过程中会产生端点效应外,对每个内禀模态函数(IMF)分量求Hilbert变换得到瞬时幅值和瞬时频率时也会产生端点效应,所以为求得Hilbert谱至少需要进行两次端点效应处理;而从上面 LMD的理论分析中知道,求得最终的时频分布只要对原信号进行一次延拓,因此理论上LMD在端点效应方面要优于HHT变换。图11所示是信号 x(t)的Hilbert谱,可以看出其相对没经过延拓的 LMD时频分布(图9)端点效应更严重,5Hz分量已完全失真,结果与理论符合。图12所示是信号x(t)采用本文方法经过两次延拓后得到的Hilbert谱,端点效应得到了较大改善,但相比于LMD方法,分解结果仍存在模态混淆现象。

5 齿轮故障振动信号分析

对于工程实际中的信号,本文方法同样能取得较好的效果。在齿轮故障试验台上采集了一段齿轮裂纹故障振动加速度信号,齿轮齿数为37,转速为420r/min,采样频率为2048Hz。图13是该信号的时域波形图,图14是该信号的频谱图,其频率成分比较复杂,无法从中清晰地提取出故障特征,因此要做进一步的分析。

采用LMD方法对该段信号进行分解,首先为了避免分解时端点效应的影响,在分解前先采用自适应波形匹配延拓法对信号进行延拓,延拓后的波形 x′(t)如图15所示,可以看出延拓部分与原信号连接光滑且波形符合原信号的自然趋势。对延拓后的信号进行LMD分解,并取与原信号对应的时间坐标,分解后得到4个PF分量和1个余量,如图16所示,可以看出,各个PF分量两端没有出现任何的发散现象,且前两个分量具有一定的故障性冲击特征。进一步对第一个PF分量P1(t)的瞬时幅值做频谱分析,结果如图17所示,从图17中可以看出在齿轮旋转频率f1=7Hz处存在明显的谱线,这说明齿轮存在局部故障,与实际情况相符。

6 结束语

针对LMD的端点效应问题,本文详细分析了其产生的原因,并提出了一种自适应波形匹配延拓法来解决。该方法依据信号内部本身的趋势与规律以及信号边界处的波形特征,利用原信号内部的子波形对信号进行延拓,使延拓后的数据保持了原信号的趋势与规律,有效地抑制了LMD分解的端点效应;同时此方法是自适应的,对于内部规律较弱、边界数据异常的信号,便只考虑信号边缘的信息,根据边缘处若干个极值点的均值来估计端点处的极值,这保证了信号在端点处的变化趋势不会发生太大的变化。从对仿真信号以及实际齿轮故障振动信号的分析结果来看,该方法能有效抑制LMD分解的端点效应。

[1]Smith J S.The Local M ean Decomposition and Its Application to EEG Perception Data[J].Journal of the Royal Society Interface,2005,2(5):443-454.

[2]Huang N E,Shen Z,Long S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non—stationary Time Series Analysis[J].Proc.R.Soc.Lond.A,1998,454:903-995.

[3]Huang N E,Shen Z,Long S R.A New View of Nonlinear Water Waves:the Hilbert Spectrum[J].Annu.Rev.Fluid M ech.,1999,31:417-457.

[4]黄大吉,赵进平,苏纪兰.希尔伯特—黄变换的端点延拓[J].海洋学报,2003,25(1):1-11.

[5]盖强,马孝江,张海勇,等.一种消除局域波法中边界效应的新方法[J].大连理工大学学报,2002,42(1):115-117.

[6]邓拥军,王伟,钱成春,等.EMD方法及 Hilbert变换中边界问题的处理[J].科学通报,2001,46(3):257-263.

[7]张郁山,梁建文,胡聿贤.应用自回归模型处理EM D方法中的边界问题[J].自然科学进展,2003,13(10):1054-1059.