微压印过程中抗蚀剂流动分析

温聚英 魏正英 熊孝东 杜 军 卢秉恒

西安交通大学机械制造系统工程国家重点实验室,西安,710049

0 引言

微压印过程就是将预先制备好的带有微结构图型的模具压入低黏度抗蚀剂薄膜,抗蚀剂在压力作用下填入模具图型的凹槽中,抗蚀剂减薄并固化,从而实现印模图型转移的过程。微压印的最终成形质量主要取决于压印中抗蚀剂的微流动和其在软模具中的填充效果,为了提高压印精度,必须对抗蚀剂在软模具中的流动机理进行研究[1]。

一些研究人员通过模拟与实验相结合的方法对微压印后抗蚀剂的填充形状进行了研究,Rowland等[2-3]对热压印过程中微米尺度抗蚀剂形貌特征进行了分析,总结出了出现单双峰模式转换的工艺条件。Heyderman等[4]、Juang等[5]对热压印过程采用流变学和有限元仿真方法,研究等温和非等温压印条件下抗蚀剂出现单双峰填充形貌的条件,并得出一个简单的二维抗蚀剂填充时间公式。Lin等[6]采用黏弹性模型分析了热压印过程中的压力分布,并进一步探讨了压印力对抗蚀剂冷却收缩的影响。Young等[7]采用黏性模型对聚苯乙烯薄膜进行了纳米尺度的热压印仿真研究,分析当位移量与压印温度不同时,抗蚀剂薄膜的变形和压力分布。贺永等[8]利用有限元方法研究了热压印过程中模具结构对抗蚀剂抗蚀剂流动形貌的影响,提出模具拓扑结构优化策略。徐敏等[9]对微压印工艺过程中的传热过程进行了传热模型数值仿真。刘红忠等[10]根据微压印过程中的力学变化特征,进一步细分压印过程,对不同复杂结构的图型压印过程进行分析研究,在理论上建立压印过程中,不同下压力下,留膜厚度随着下压速度、加速度及下压时间的变化关系。但是目前研究都集中于热压印过程中高抗蚀剂的填充状态,进行有限元仿真时忽略滑移边界条件及表面张力对抗蚀剂填充的影响,对常温微压印过程中低黏度抗蚀剂流动状况分析国内外未见报道。本文采用有限元方法系统分析了微米尺度下的不同工艺条件和模具结构,考虑滑移边界条件和表面张力对低黏度抗蚀剂流动形貌的影响,并进行压印实验,从而为提高微压印精度提供理论指导。

1 常温微压印过程中抗蚀剂流动有限元分析

1.1 抗蚀剂流动有限元模型建立

1.1.1 几何模型建立

根据微压印工艺过程,建立适合常温微压印过程的几何模型,图1为抗蚀剂成形三维模型图。在微图型模板中,z方向的特征长度远远大于图型截面的特征长度,故可将其简化为二维应力应变问题,简化的二维网格几何模型及其边界条件设定如图2所示。图1中,横截面宽度方向为x轴,沟槽深度方向为y轴,h0为抗蚀剂薄膜初始厚度,hc为压印模具表面特征图型深度,hr为抗蚀剂留膜厚度,Si为第i个特征图型的宽度,Wi为第i个沟槽的宽度,S为压印模具横向宽度。有限元几何模型主要由软模具(硅橡胶材料)、抗蚀剂(低黏度抗蚀剂)及基底(硅片)三部分组成。硅片作为基底固定不动,软模具相对于硅片垂直向下运动。

微尺度下,抗蚀剂与硅片基底之间界面B1具有滑移现象。在压印实际过程中,抗蚀剂填充沟槽是处于开放状态的,将抗蚀剂薄膜两侧边界B2设为对称边界,抗蚀剂填充沟槽的过程是开放而非封闭的模型。自由界面B3是抗蚀剂薄膜上表面,即抗蚀剂与空气接触界面,受表面张力的作用。随着模具下压运动,抗蚀剂与软模具内壁面B4接触,抗蚀剂与软模具表面有润湿作用,具有一定的接触角。

微图型模板的占空比α是抗蚀剂填充状态出现单双峰及压印精度的重要参数,定义其为沟槽宽度之和与微图型模板总宽度的比值;模具深厚比β为沟槽深度与抗蚀剂初始厚度的比值;宽厚比γ为沟槽宽度与抗蚀剂初始厚度的比值;深宽比δ为沟槽深度与沟槽宽度的比值,即

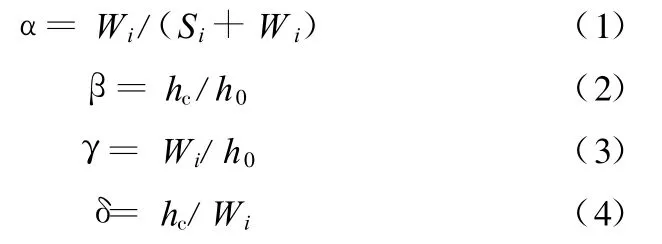
为了研究抗蚀剂填充效果,本文拟采用填充度评价抗蚀剂微压印精度。填充度ε为抗蚀剂填充面积At与沟槽填充面积Aw的比值,即

1.1.2 抗蚀剂数值模拟过程条件的设定

在压印光刻技术中,大部分特征尺寸已经达到微纳米级,在如此小尺寸下,液体表面张力的影响已经不可忽略,即当特征尺寸较大时,体积力起主导作用;当特征尺寸很小时,表面力起主导作用。固体表面能的作用在微尺度下作用突出。液体相对于固体表面的润湿性会严重影响微流体的流动特性。微压印过程中抗蚀剂流动模型的条件总结设定如下:①模具垂直于硅片运动,速度为2μ m/s;②自由表面张力系数为0.68,考虑表面张力和惯性力的影响;③考虑抗蚀剂与硅橡胶的接触角,即硅橡胶与抗蚀剂的黏附特性及表面浸润性,考虑抗蚀剂与模具结构的滑移边界条件;④对自由表面利用Lagrange和adaptive remeshing方法进行网格重构。

自由表面与模具接触需要通过接触检查运算法则进行检验。惩罚因子与滑移系数为10—9,渗透因子为0.2,网格偏差为0.3,时间步长为0.01,收敛精度为0.001,选用隐格欧拉方法进行迭代。

1.2 抗蚀剂流动的影响因素分析

常温微压印过程中,影响抗蚀剂流动填充成形的因素很多,如壁面滑移、抗蚀剂的表面张力、抗蚀剂材料、压印速度及模板结构等,这些因素直接影响着微压印的精度。

1.2.1 壁面滑移对抗蚀剂流动的影响

微压印过程中,由于图型模板结构的特征尺寸微小,故抗蚀剂充模流动时的阻力大为增大,需用较大的模板压力来克服各种阻力。这使得抗蚀剂在通道壁面处所受的剪切应力明显增大,强烈的解缠作用使得大分子之间的相互吸引力减弱,靠近壁面的分子和本体一起移动,导致抗蚀剂在壁面处发生壁面滑移。随着剪切应力的增大,壁面滑移对抗蚀剂流动的影响增大。

当模具下压0.6μ m时,完全滑移与无滑移边界条件下的抗蚀剂对模具壁面的压力如图3所示。

由图3可知,无滑移边界条件的压力梯度小于存在滑移边界条件时的压力梯度。随着特征尺度的减小,壁面滑移现象对抗蚀剂流动影响增大,在仿真时必须予以考虑。

1.2.2 表面张力对抗蚀剂填充的影响

研究表明,由于表面张力是液体的一个重要参数,特别是在微尺度下,表面张力起到了主导性的作用,图4反映了表面张力对抗蚀剂填充的影响。

图4表明,在相同的下压条件和填充时间下,在无表面张力的时候,抗蚀剂更容易填充到软模具的凹槽中,且填充的效率更高,这对于深宽比较大的软模具影响明显,故实际的压印过程中,应考虑表面张力带来的影响。

1.2.3 模板下压速度对填充度的影响

常温微压印过程中,模具下压速度是直接影响抗蚀剂填充时间及填充速度的重要参数。本节选用占空比α=0.875的矩形槽结构模板,在模板下 压 速 度 分 别 为 0.5μ m/s、1μ m/s、2μ m/s、10μ m/s,其他条件相同时,比较不同下压速度对抗蚀剂填充度的影响,如表1所示。

表1 不同下压速度时抗蚀剂填充度比较

由表1可知,模具速度降低可使抗蚀剂填充度提高。模具速度低时,没有单双峰现象出现;模具速度越高,单双峰现象愈明显,如没有足够的保压时间,矩形槽结构边缘就无法填充满。这是由于速度较低时,沟槽约束空间内的空气有足够的时间逃逸出去,抗蚀剂能够较好的填充沟槽棱角。因此,在保证填充效率的同时,应使尽量降低速度,使抗蚀剂可以较好地填充槽结构,从而获得更高的压印精度。

1.2.4 占空比对抗蚀剂填充形貌的影响

(1)非对称模板结构下抗蚀剂的填充形貌。当抗蚀剂厚度、模具总宽度、模具运动速度都相同时,随着模具沟槽宽度的减小,抗蚀剂填充形貌的变化如图5所示。

由图5可看出:随着占空比的减小,抗蚀剂填充形貌逐渐由双峰向单峰转变。当填充形貌呈双峰时,较大特征图型宽度下方的抗蚀剂的流动速度较高。模具下压时刻相同,占空比越小,高度差越大。随着压印时间的增加,两个峰值高度差也越来越大,距模具壁面较近的峰先到达槽顶部。

(2)对称模板结构下抗蚀剂的填充形貌。选择占空比为0.375的对称模板结构,抗蚀剂初始厚度为 12.5μ m,模板以2μ m/s速度向下运动时,不同时刻抗蚀剂的填充形貌如图6所示。

由图6可知,随着模具下压运动,抗蚀剂自由液面越来越陡峭,双峰逐渐向沟槽中心移动;当抗蚀剂接近沟槽顶端时,双峰慢慢重合消失,少量的抗蚀剂往沟槽边缘填充运动;较窄沟槽中抗蚀剂单峰突起趋势越来越明显。当占空比较小时,抗蚀剂受挤压的部分变大,受迫流向压力较小区域的抗蚀剂增多,垂直流动收缩到模穴中央形成单峰流动形貌;占空比较大时,由于表面张力和惯性力的影响,受迫流动对中部的贡献较小,使得抗蚀剂在压入模具产生膨胀凸起,垂直流动主要沿着沟槽侧壁运动,出现双峰。如果压印的时间不够,单双峰没有压平,会使压印的压印精度较差,成形存在缺陷。

1.3 抗蚀剂流动填充效果分析

本文采用填充度、填充高度及填充时间评价抗蚀剂填充效果。抗蚀剂初始厚度和模板结构对抗蚀剂填充效果影响很大。本节主要从占空比、宽厚比等因素的角度分析抗蚀剂的流动规律。

1.3.1 宽厚比对单双峰转换的影响

模板结构占空比一定的情况下,分析抗蚀剂初始厚度对抗蚀剂填充的影响。定义宽厚比γ为横坐标,即横轴;抗蚀剂峰值距离最近沟槽壁面的距离Wx与槽宽Wi的比值ψ为纵坐标,即纵轴。抗蚀剂单双峰模式与宽厚比关系曲线如图7所示。

选择占空比为0.625,两槽宽W1、W2分别为2.5、25,抗蚀剂厚度 h0 分别为 10、12.5、15 、20、30、50。压力与留膜厚度关系曲线如图8所示。

峰值距离沟槽壁面越近,双峰现象越明显。由图7可知,宽厚比小于1时,抗蚀剂形貌出现单峰。随着宽厚比的增大,抗蚀剂形貌由双峰转换为单峰。宽厚比决定着抗蚀剂水平和垂直变形运动。由于抗蚀剂受到底面边界约束的影响,随着宽厚比的增大,流动需要克服的阻力增大,导致流动不够充分,无法影响到较远的区域,使得靠近模具沟槽的壁面迅速隆起,双峰现象明显。随着抗蚀剂初始厚度减小,边界效应越来越明显,模具压力越来越大,这样才能保证抗蚀剂填充精度。但另一方面,从工艺的角度来说,宽厚比不能一直无限制地减小,也就是说,抗蚀剂的初始厚度无限制地增加不利于工艺优化,从留膜厚度和模具压力的关系曲线来说,当留膜厚度大于 3.5 μ m 的时候,模具压力变化不大。因此,在保证有足够的抗蚀剂填充到凹槽中的同时,可留有3.5μ m的残余膜厚,从而使得宽厚比更为合理。

1.3.2 占空比和深厚比对抗蚀剂填充效率的影响分析

选择深厚比 β分别为 0.20、0.66、1.00,改变模具的占空比,抗蚀剂到达宽槽顶端的填充时间比较如图9所示。

由图9可知,随着占空比的增大,所需的填充时间越长;对比图中的三组曲线,相同占空比的情况下,深厚比为1时的填充时间较长。在实际的工艺中,在不影响填充效率的前提下,可以选择较小的深厚比,即通过增加初始膜厚来提高压印的填充效率。

1.3.3 抗蚀剂流动对变形的影响

实际压印过程中,由于软模具材料为硅橡胶,故抗蚀剂填充沟槽过程中抗蚀剂流动对软模具也是有影响的。在此选择占空比α为0.5和0.75的模具,其他工艺条件相同的情况下,分析软模具的变形与抗蚀剂填充度的关系,如图10所示。

由图10可知,随着抗蚀剂填充度的增大,软模具变形增大。模具x方向变形量明显比y方向变形量大,约达到y方向变形量的三倍。当抗蚀剂填充度达到90%时,模具变形率开始增大,成直线上升。因此抗蚀剂填充沟槽过程中,软模具受力较小,其变形也小,可以忽略填充过程中抗蚀剂与软模具的相互作用力。但当抗蚀剂填充沟槽状态为过填充时,模具受到抗蚀剂作用力较大,所受应力大。可用石英玻璃衬底和增大抗蚀剂初始厚度来减小软模具的变形,减小其对抗蚀剂压印精度的影响。

2 实验验证

选择两种不同特征结构的模具进行实验,图型特征宽度和高度相同,沟槽宽度不同。模具图型特征结构如图11所示。两种模占空比分别为0.67和0.30,对不同的模具选择不同的匀胶参数,占空比较大的甩胶薄膜厚度较厚。具体的匀胶实验参数如表2、表3所示。

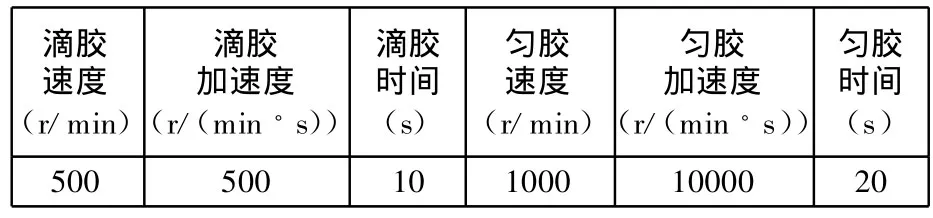
表2 模具a匀胶工艺参数

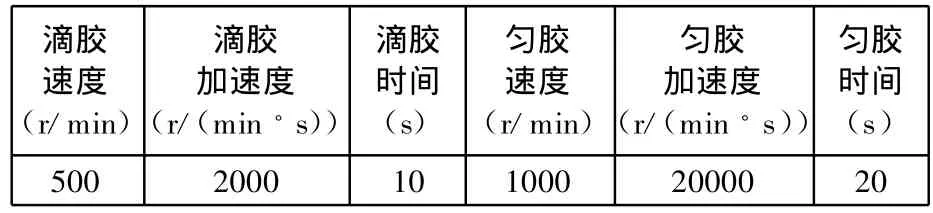
表3 模具b匀胶工艺参数

在压印的过程中,软模具以2μ m/s的速度下压,当在压力表上显示的压力发生较大的跳动时,结束下压,并进行紫外曝光固化,固化时间为600s,取下模具,结束压印。

选用三维扫描共聚焦显微镜及台阶仪测量模具下压不同位移时压印后的抗蚀剂形貌。使用模具a和模具b进行压印实验,抗蚀剂填充形貌实验结果如图12和图13所示。

从图12和图13中可看出,采用共聚焦显微镜和台阶仪测量的抗蚀剂沟槽底部不平整,这是由于本实验所采用的硅橡胶模具是外协制作母版翻制而成的。母版是由激光刻蚀加工而成,激光加工的槽低不平整,因此翻制出来的硅橡胶软模具特征图型也是不平整的。采用此模具进行压印实验,固化后的抗蚀剂沟槽底部也是不平整的,图型结构与母版是相同的。同时由图12a可知,在沟槽顶端与底部之间出现了低于沟槽低端的尖峰,这个尖峰可能是由于软模具与抗蚀剂相互作用,抗蚀剂在微尺度下表面张力和剪切力相对占主要地位,使得抗蚀剂在模具挤压和剪切作用力非常大的区域,抗蚀剂未能及时填充此区域而产生的。

由图12和图13可知,在距离沟槽边缘,抗蚀剂分别出现了单双峰。选择模具a进行压印实验,甩胶厚度较厚时,较窄沟槽内出现单峰,窄宽沟槽内出现双峰(图12)。即宽厚比小于1时,出现单峰,宽厚比大于1时出现双峰。对于模具b,甩胶厚度较薄时,较窄沟槽内出现单峰,窄宽沟槽内出现双峰(图13)。

3 结论

(1)在考虑壁面滑移、抗蚀剂的表面张力的情况下,研究模板微图型占空比、宽厚比对抗蚀剂填充形貌的影响规律及单双峰模式出现的转换曲线。抗蚀剂填充出现的双峰现象不利于压印精度的提高和稳定性,应尽量避免出现双峰现象。

(2)微图型模板结构是影响抗蚀剂填充状态的重要因素,宽厚比综合决定抗蚀剂水平、垂直运动变形及峰值位置。宽厚比小于1时,抗蚀剂填充形貌出现单峰。深厚比一定,随着占空比的增大,填充时间越长。在不影响填充效率的前提下,可以选择较小的深厚比,即通过增大初始膜厚来提高压印的填充效率。

[1]Scheer H C,Schulz H.A Contribution to the Flow Behaviour of Thin Polymer Films during Hot Embossing Lithography[J].Microelectronic Engineering,2001,56:311-332.

[2]Rowland H D,King W P.Polymer Deformation and Filling Modes during Microembossing[J].Journal of Micromechanics and Microengineering,2004,14:1625-1632.

[3]Rowland H D,Sun A C,Schunk P R,et al.Impact of Polymer Film Thickness and Cavity Size on Polymer Flow duringEmbossing:toward Process Design Rules for Nanoimprint Lithography[J].Journal of Micromechanics and Microengineering,2005,15:2414-2425.

[4]Heyderman L J,Schift H,David C,et al.Flow Behaviour of Thin Polymer Films Used for Hot Embossing Lithography[J].Microelectronic Engineering,2000,54:229-245.

[5]Juang Y J,Lee L J,Koelling K W,Rhelolgieal Analysis of Polyvinyl Butyal Near the Glass Rnasition Temperature[J].Ploymer Engineering and Seienee,2001,41:275-289.

[6]Lin C R,Chen R H,Hung C.The Charaeterization and Finite—elementAnalysis of a Polymer under Hot Pressing[J].Advanced M anufaeturing Technology,2002,20:230-235.

[7]Young W B.Analysis of the Nanoimprint Lithography with a Viscous Model[J].Microelectronic Engineering,2005,77:405-411.

[8]贺永,傅建中,陈子辰.聚合物微流控芯片热压成型的建模研究[J].浙江大学学报(工学版),2005,39(12):1911-1914.

[9]徐敏,罗怡,王晓东,等.聚合物微结构热压成形温度有限元分析[J].传感技术学报,2006,19(5):2015-2017.

[10]刘红忠,丁玉成,李涤尘,等.微细加工中的快速压印研究[J].机械工程学报,2006,19(5):114-117.