冗余驱动盾构机推进系统机液耦合模型及载荷特性分析

丁 晟 余海东 王 皓

上海交通大学机械系统与振动国家重点实验室,上海,200240

0 引言

盾构机是集机械、电气、液压、测量、控制等多学科技术于一体且专用于地下隧道工程开挖的技术密集型重大工程装备。为了满足巨大的工作载荷,盾构机通常采用冗余驱动的方式进行掘进,但这同时会造成驱动力分配不平衡,在复杂多变的地质情况下,容易发生堵停事故[1]。

近年来随着盾构机技术的不断发展,国内外学者在其推进系统研究方面取得了一定成果。在机械系统方面,Sugimoto等[2]建立了考虑摩擦与动平衡的全盾体动力学模型并验证了其有效性,Komiya等[3]建立了主要考虑刀盘对外载响应的有限元模型,Marshall等[4]研究了推进缸结构对运动和力的影响。这些研究主要集中在机械结构,没有考虑液压控制部分。在液压系统方面,施虎等[5-6]分别建立了压力控制和速度控制模型,分析了各参数对于压力和速度特性的影响。他们的研究没有考虑机械系统的载荷传递特性,且系统稳态假设在导致堵停事故的极端工况外载下并不适用。

本文以直径为6280mm的某型土压平衡盾构机推进系统为研究对象,分别建立考虑冗余驱动机械系统动力学模型和单组液压系统的液压模型,在此基础上建立冗余驱动盾构机推进系统机液耦合模型;给出外载与液压调速阀开度值之间的关系,利用MATLAB/Simulink模块对变载荷下含速度—外载反馈和不含反馈条件下冗余驱动各组推进缸载荷特性进行分析,揭示盾构机堵停现象产生机理,为其控制策略提供依据。

1 盾构机推进系统机液耦合模型

1.1 几何模型及载荷

盾构机盾体部分的主体结构如图1所示,它由16个液压缸进行推进,刀盘在切削过程中,受到岩土施加的载荷,由盾体的前部传递到各个推进缸上,各个推进缸前端与盾体固接,后部通过球铰连接后作用在管片上,为了便于控制,一般将16个液压缸分为4组,由于重力的作用和掘进过程中泥土主要分布在下半部分的原因,液压的控制分组并不对称,下部的液压缸数目一般比上部多,左右液压缸的数目和位置一般对称,如图2所示。

建立三维直角坐标系oxyz,如图3所示,原点o位于刀盘切削平面的中心,z轴正方向为掘进方向,y轴正方向为重力方向的反方向,x轴正方向为水平向右。

设4个分组区域内单个液压缸的载荷分别为F1、F2、F3、F4,同组的液压缸共用一个控制系统,回路状态及输出载荷保持相同。根据各个液压缸的几何位置得到4个区域内等效推进力为5F1、4F2、4F3 和 3F4,等效弯矩为 M1 、M2、M3 和 M4,如图3所示。盾体与刀盘之间通过一个三排止推轴承连接,设刀盘受到的推进方向阻力为Fz,刀盘平面内的弯矩为Mx和My。

1.2 冗余驱动机械系统模型

根据上述载荷分布,不考虑构件弹性变形和姿态偏转,即只考虑掘进方向上的一个自由度,在oxyz中建立力学平衡方程:

式中,z¨为盾构机掘进方向的加速度,由液压系统得出;r为推进缸中心点在xy平面内与盾构中心点的距离;m为被推进部分总质量;Fz为掘进方向的阻力;Mx、My分别为x轴、y轴方向盾构机所受的弯矩。

式(1)可以写成矩阵形式:AX=B,其中系数矩阵A包含了机构的几何信息,X为包含驱动力的未知向量,B为惯性力向量。未知量个数为4,方程个数为3,因此解不唯一。

令A+为A的Penrose pseudo广义逆,则X=A+B为矩阵方程的最小范数解。其物理意义是完全满足运动协调条件的同时使驱动力的平方和最小。然而对于实际的盾构机推进系统,由于没有协调机构,完全靠控制系统来减小误差,无法达到精确的运动协调,无法完全满足运动协调条件,因此由最小范数解求得的驱动力与实际情况不符。

盾构机控制系统往往不直接调节推进缸行程,而是通过控制驱动力的方式来控制运动误差。各组推进缸通过一定的控制算法不断改变驱动力以靠近控制目标值,以此来减小运动误差。

引入c(t)=[c1(t)c2(t)c3(t)c4(t)]T为各组推进缸驱动力的控制目标值,将问题转化为求驱动力与控制目标力之差的最小范数min‖X—c(t)‖,则目标优化函数为

构造拉格朗日函数:

令

联立式(1)、式(3)解得

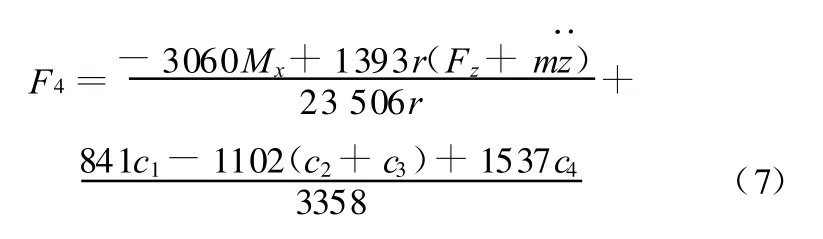
1.3 液压系统模型

盾构机推进系统的液压回路一般由比例调速阀和比例溢流阀分别进行速度与压力控制[5],在此对单缸液压系统进行建模,液压回路元件主要考虑调速阀,溢流阀只考虑流回油缸的体积流量qVc,系统结构如图4所示。

由调速阀机构原理图(图5)可知,调速阀由减压阀与节流阀串联而成,减压阀能保持节流阀两端压差不变,从而使通过节流阀的流量不受负载变化的影响。减压阀参数中的阀口开度δ决定了流经减压阀的流量。由于实际物理结构的限制,δ只能在一定范围内变化。令其变化的最大值为δmax,可根据阀的型号从机械设计手册中查得。

液压系统工作时,将减压阀阀口开度值分为两个区域(δ＜δmax和δ=δmax,δ、δmax分别为减压阀阀口开度、最大开度)来讨论,这两种阀口开度值会导致液压回路出现两种不同状态,须分别对其建立压力与流量关系方程:

(1)当δ＜δmax时,推进缸匀速推进,即v=v0。在控制系统的作用下,驱动力由外载决定。因此,对于液压缸,有

式中,p1为液压缸无杆腔压力;A1为液压缸无杆腔的面积;Fr为液压缸活塞所受外载。

对于节流阀,有

式中,qV为液压回路体积流量;Cd1为节流阀阀口流量系数;d1为节流阀滑阀直径;h1为节流阀阀口开度;ρ为液压油密度;p2为减压阀出口压力。

对于减压阀,有

式中,Cd2为减压阀阀口流量系数;d2为减压阀滑阀直径;p3为液压泵出口压力。

联立式(8)～式(10),可得回路流量qV和减压阀阀口开度δ。

(2)当δ=δmax时,推进缸输出最大驱动力减速推进。δ随回路载荷的增大而增大,达到最大值后保持恒定,此时δ=δmax,代入式(8)～式(10)得到流量方程:

式中,qVmax为液压回路最大流量;As为节流阀端口面积;Amax为阀口开度达到最大时的减压阀端口面积。

此时p3保持恒定,而 p1还在增大。由式(11)易得回路流量会减小,从而导致推进速度的减小。液压缸的推进速度与流量的关系如下:

1.4 机—液耦合系统模型

前面对于推进系统机械结构进行建模,得到了外载从刀盘到各组推进缸的传递情况,建立了单个液压缸的液压模型,得到了载荷在液压回路内部的传递情况。由于同组内的各个液压缸共用一个液压回路,故单缸模型与单组模型等同。

将冗余驱动机械系统模型与4组液压回路模型通过数值算法联结成一个整体,可得到整个机—液耦合推进系统模型。

联立式(4)～式(11)得到4组液压回路的减压阀阀口开度与外载关系如下:

设h为仿真步长,Fh为总驱动力(Fh=5F1+4(F2+F3)+3F4),F(j)h为第j仿真步的总驱动力,则相应的数值算法步骤如下:

(2)Fz、Mx、My为外载输入,并令z¨=0,将其代入式(4)～式(7)解得满足平衡条件的驱动力。令式(5)中的Fr=Fi,求得各组液压缸活塞杆压力和无杆腔压力。将代入式(9)、式(10)算出液压系统的流量,将代入式(13)得到,转入步骤(1)。

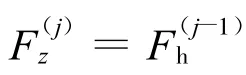
式中,K1、K2分别为推力系数、转速系数;W为总推力;πR2P为土箱压力;W0为摩擦阻力;n为刀盘转速。

式(13)是一个分段函数,表明了各组液压回路状态与外载之间的分段关系,而各组液压回路状态决定了整个推进系统的状态。

因此,基于式(13)提出以δi为核心的系统状态判定方法:当某组δi达到极值δmax时,认为系统总驱动力Fh不能满足外载的需要,系统发生堵停。可用步骤(3)得到的推进速度v(j)关于时间的曲线来验证判定方法是否准确,并用速度变化的快慢来描述堵停的严重程度。

2 数值仿真模型

2.1 模型

根据上述系统模型及算法,在 MAT LAB/Simulink模块中进行数值建模与仿真,如图6所示。选取固定步长为0.02s,Bogacki—Shampine求解器,仿真时间为10s。

设定参数如下:预设掘进速度v0=1mm/s,液压缸无杆腔的面积A1=49 100mm2,节流阀端口面积As=34.6mm2,阀口流量系数Cd1=Cd2=0.7,节流阀滑阀直径d1=10mm,减压阀滑阀直径d2=5mm,液压油密度ρ=900kg/m3,节流阀阀口开度h1=1mm,减压阀阀口最大开度δmax=0.7mm,推进缸中心点在 xy平面内与盾构中心点的距离r=2792mm。

2.2 载荷

由于岩土力学特性和失效方式差异,盾构机在异质岩土掘进时,刀盘上推进阻力和弯矩会随着刀盘的旋转发生变化,使得冗余驱动推进系统各组液压缸需要进行调整以获得最优的掘进效率。文献[8]得到盾构机在异质岩土掘进工况下的刀盘推进阻力和弯矩,本文基于该结论,进一步假设由于某种原因导致推进阻力上升,我们给出刀盘所受弯矩和推进阻力,分别如图 7、图8所示。

3 载荷特性分析

仿真可得各组液压回路的驱动力、推进速度、流量、压力等特性曲线,选取其中某些结果进行分析。

如图9所示,约在8.4s时,δ3达到最大值δmax,根据上述判定方法判定系统进入堵停状态。在图10中得到验证,从8.4s开始,第三组推进缸推进速度迅速减小,盾构机发生堵停现象。

推进速度减小后,由于反馈的作用导致外载减小,由图11可见,F1、F2、F43组驱动力反而略有减小。相应地在图9中,只有其中一组的阀口开度δ达到最大值,此后其余各组的δ反而减小。

因此,在总驱动力不能平衡外载阻力而出现减速推进时,若干分组推进缸的驱动力尚有一定裕度。此时,可以调节控制目标ci(t),使驱动力重新分配,使系统恢复正常工作状态。

由于土层条件的不同,速度对外载的反馈程度存在较大差异。当反馈系数过小时,速度减小带来的土层阻力减小量小于外载自身的增加量,我们将这种情况称之为欠反馈,考虑这种情况进行仿真,得到各组液压缸推进阻力曲线以及减压阀阀口开度曲线,如图12、图 13所示。

在图13中,各组δ值接连达到最大值δmax,可知盾构机发生堵停,其推进速度迅速降低至零。

通过对图12中各组推进阻力曲线之间的比较,可总结出弯矩对系统状态的影响规律:对于Mx,由于F1、F42组驱动力的液压缸数不同(5个、3个),比较容易利用缸数差来达到平衡;对于My,由于F2、F3液压缸数目相同(都是4个),两组都输出最大驱动力来克服巨大阻力Fz,难以用两组驱动力差值来平衡弯矩。体现在仿真结果上,F1与F4的值相差不大,而 F2与F3的值相差较大。

通过比较两种条件下的仿真结果,可知减压阀阀口开度特性曲线能有效反映外载变化对液压回路的工作状态的影响。由仿真结果验证可得,上述基于式(13)的以δi为核心的系统状态判定方法有效,可为盾构机异质岩土掘进时驱动力分配的控制提供依据。

4 结论

(1)堵停现象本质是液压元件达到极限值时回路流量减小造成的执行元件减速。而冗余驱动带来的驱动力平衡分配问题是主要原因之一。

(2)减压阀阀口开度值体现了外载及系统状态的变化,可以根据该值对系统状态进行判定。

(3)根据本文所述的由δi评价系统状态的方法得到各组液压回路的状态,实时调节控制系统目标值ci(t)制定相应控制策略实现自动防堵控制。这样可减小现场驾驶员操作难度,避免事故发生。

[1]宋天田,肖正学,苏华友,等.上公山TBM施工2.22卡机事故工程地质分析[J].岩石力学与工程学报,2004,23(增刊1):4544-4546.

[2]Sugimoto M,Sramoon A.Theoretical Model of Shield Behavior during Excavation.I:Application[J].Journal of Geotechnical and Geoenvironmental Engineering,2002,128(2):138-155.

[3]Komiya K,Soga K,Akagi H,et al.Finite Element Modelling of Excavation and Advancement Processes of a Shield Tunneling Machine[J].Soils Found.,1999,39(3):37-52.

[4]Marshall M A,Milligan G W E,Mair R J.Movements and Stress Changes in London Clay Due to the Construction of a Pipe Jack[C]//Geotechnical Aspects of Underground Construction in Soft Ground.Rotterdam:Proc.Int.Symp.,1996.

[5]施虎,龚国芳,杨华勇.盾构掘进机推进压力控制特性分析[J].工程机械,2008,39(5):23-26.

[6]施虎,龚国芳,杨华勇.盾构掘进机推进速度控制性能分析[J].机床与液压,2008,36(8):77-79.

[7]张厚美,吴秀国,曾伟华.土压平衡时盾构掘进试验及掘进数学模型研究[J].岩石力学与工程学报,2005,11(增刊2):5762-5766.

[8]曾晓星.异质岩土工况下土压平衡盾构载荷等效及传递特性研究[D].上海:上海交通大学,2009.