基于摩擦功原理的高副滑动磨损的研究

章易程 田红旗 唐进元 李 蔚 林英豪 陈 广

1.中南大学,长沙,410004 2.东南大学,南京,211189

3.中国南车集团戚墅堰机车车辆工艺研究所,常州,213011

0 引言

在实际的应用中,相对运动的高副不可避免磨损,即使闭式传动的机车齿轮也存在滑动磨损[1-2]。高副滑动磨损的研究面临着两方面的问题:一是由于滑动磨损机理往往是黏着磨损、磨粒磨损等机理综合作用的结果,难以采用单一磨损机理来描述磨损状态[3-4];二是由于高副轮廓往往因磨损而动态变化[5],难以采用手工计算来描述磨损状态,齿轮副还会因其啮合刚度的变化而引起齿轮副间载荷分配的变化,从而使齿轮副磨损的计算变得更为复杂。一些学者采用数值仿真技术有效地描述了齿轮副磨损过程的动态变化规律[6-10],但大都没有详细地考虑影响齿轮副间受力分配的啮合刚度变化,而且几乎都是采用基于黏着磨损这一单一机理分析下推导的Archard磨损公式,理论依据不充分,计算也过于复杂。为此,本文推导了基于摩擦功原理的滑动磨损计算公式,并以东风8B机车齿轮副为例,在充分考虑轮齿刚度、轮廓曲线等参数动态变化的情况下进行了仿真分析,试图研究一个原理可靠、简单、实用的高副滑动磨损计算公式。

1 滑动磨损公式

黏着磨损与磨粒磨损,都是由于滑动摩擦使得一部分功用于克服黏着磨损的黏着力、磨粒磨损的剪切力而被消耗掉,即摩擦力F所做的功消耗在破坏材料分子的结合上,并以热能或声能的形式出现。如图1所示,设在dt时间内,高副元素齿廓1从接触点J′(1)到接触点J″(1)的运动距离为ds(1),接触点法向磨损深度为dh(1),脱落材料体积为dV(1);同时,高副元素齿廓2从接触点J′(2)到接触点J″(2)的运动距离为ds(2),接触点法向磨损深度为dh(2),脱落材料体积为dV(2)。假设稳定工况下摩擦力所做的功dW与脱落的材料体积dV成正比,则对于高副元素齿廓1有

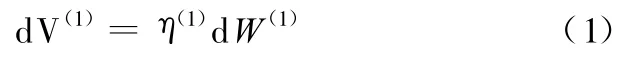
式中,η(1)为磨损系数,表示单位摩擦功将产生的齿轮1磨损体积,它与材质、硬度、润滑情况及工况等条件有关。

通过摩擦磨损试验机可以测量出某一高副元素磨损体积与磨损功后,两者相比即可求出其磨损系数。高副元素齿廓2对高副元素齿廓1所做的摩擦功为

高副元素齿廓2对高副元素齿廓1产生的摩擦力为

式中,f为摩擦因数;N为接触点上的正压力。

在dt时间内,若两高副元素接触宽度为db(1),则高副元素齿廓1磨损的体积为

由式(1)～式(4)可得

令

当一对高副元素接触宽度始终保持为B时,可以取db=B。则式(5)可以改写为

同理有

式中,ε(1,2)、ε(2,1)分别为高副元素齿廓1对高副元素齿廓2的相对滑动系数和高副元素齿廓2对高副元素齿廓1的相对滑动系数,初次接触的相对滑动系数计算以理论轮廓为依据[11-12]。

当齿轮转速为n时,齿轮每转动一圈齿廓便重复接触一次,则当运转时间步长为dt时,齿廓表面J点的接触次数为ndt。当经过M个时间步长后,J点的磨损深度为

式(8)表明,最终磨损深度为每一磨损步长产生的磨损深度的矢量和在初始轮廓法线上的投影大小。

式(8)与Archard磨损公式相比,相同的是,磨损系数、相对滑动系数(距离)与受力大小均成正比地影响着高副元素磨损的大小,具有殊道同归的效果,但摩擦功原理并不局限于单一的黏着磨损或磨粒磨损,其概括性强与依据更可靠;不同的是,式(8)增加了反映重要摩擦性质的摩擦因数,表明摩擦因数正比地影响着高副元素磨损的大小。

式(8)避免了文献[9-10]计算Hertz应力,以及通过离散Hertz接触宽度来计算Hertz接触小单元上磨损的烦琐。为保证计算精度,当轮廓离散点密至相邻两点距离接近Hertz接触宽度时,也就等效于考虑了Hertz接触上的小单元累积磨损。

为了保证齿轮的连续传动,齿轮的重合度往往大于1,则在啮合传动过程中,会出现单双对齿轮副交替啮合的情况,从而存在正压力NI,J在两对齿轮副间分配的问题[13]:

式中,KI,J为齿轮副刚度,当其为单对齿轮副刚度时采用当量齿形法计算[13-14]。

2 磨损仿真

2.1 仿真过程说明

在仿真计算过程中,通过建立图2所示的坐标系来计算磨损过程中齿廓曲线各离散J点的坐标[10]。其中,o1xy为固定坐标系,其纵坐标通过齿轮1的回转中心;o1x1y1为与齿轮1固结在一起的动坐标系;o2x2y2为与齿轮2固结在一起的动坐标系。

根据坐标可以求得运动距离为

对于新形成齿廓的每个点来说,应该遵守包络条件。如果在第一对啮合的齿廓上的第(J—1)点与第(J+1)的齿廓点不相互嵌入,则必须满足:

如不满足式(11),则邻接点取代J点接触。

仿真流程图如图3所示。一般来说,时间步长越短,轮廓离散的点数越多计算越准确,但计算时间越长。为了寻找磨损变化的规律与提高计算速度,本仿真实验选取磨损步长为10h,齿廓曲线离散成24个等分点。计算参数如表1所示,为便于对比磨损状况,两齿轮取相同的磨损系数。

表1 东风8B机车牵引齿轮副磨损计算参数[15]

2.2 仿真结果与分析

图4所示以理论渐开线齿廓计算的相对滑动系数在节点处为0,这是由于节点处齿廓作相对纯滚动的原因。图5所示小齿轮廓的各步长内平均相对滑动系数总体比大齿轮廓相对滑动系数大,这主要是由于小齿轮廓每次自身滑移距离较小所致。图6、图7表明刚度与载荷的变化明显对应于单双对齿轮副的交替啮合,且随着磨损的加剧,啮合刚度有所下降,由于齿根磨损严重而在齿根啮合处啮合刚度下降相对明显些,此处齿轮副承担的载荷减小的程度相对大些,但由于单齿区不存在载荷分配问题使得齿轮副承受的载荷大小几乎不因磨损而变化。如图8所示,由于刚度的影响,使得齿廓的初始磨损深度变化也明显对应于单双齿轮副的交替,但随着时间的推移,由于相对滑动系数与包络情况的综合影响,单双齿交替位置的磨损界限变得模糊;由于相对滑动系数的影响,齿根部出现最大的磨损量,而节点处的磨损量为0,但实际中会由于节点承受的压应力大导致压溃而磨损;此外,由于小齿轮的轮齿啮合次数多而造成小齿轮廓的磨损程度远远大于大齿轮廓的磨损。图9的磨损总量是指单一齿廓在一定时间内各啮合点磨损深度的累加,它表明由于早期表面光滑而初期磨损总量往往很小,随后由于早期磨损造成的表面不光滑而出现磨损加剧的跑合阶段,然后经跑合后的表面又变得光滑而出现稳定磨损阶段,磨损程度在跑合与稳定磨损两阶段交替进行。图10表明齿廓上各步长内磨损总量在跑合阶段最大,且磨损总量的大小交替变化。图11表明,第一个磨损步长内的传动比即为理论的恒定传动比(—17/76),而在第30个磨损步长内,齿廓不再是渐开线形状,从而出现瞬时传动比[10]围绕理论传动比波动的现象,有时传动比为正是由于齿廓某处磨损大出现邻接点取代理论接触点,从而造成从动齿轮回转的缘故。仿真磨损规律与实际情况一致,也与其他学者的实验研究情况[6,16-17]相吻合。

由图11的可知,监控传动比的变化可定性地了解齿轮的磨损状态。通过上述分析并根据文献[12-13]可知,通过变位使大小两齿轮副齿根处的相对滑动系数尽量靠近,同时通过选材与热处理等方式提高小齿轮的耐磨性,从而可以使得两齿轮达到等寿命使用。通过改善润滑性能与提高表面加工精度可以延长整个齿轮副的使用寿命。通过大小两轮齿数的奇偶相配,可以实现齿表面的均匀磨损。

3 结论

(1)基于摩擦功的高副滑动磨损计算公式从能量的角度高度概括地反映了滑动高副摩擦磨损的规律,理论依据充分。

(2)基于摩擦功的摩擦磨损计算公式简单实用,适应于高副摩擦磨损的动态仿真分析。

(3)最终磨损深度为每次磨损深度的矢量之和在初始轮廓法线上的投影长度。

[1]陶征毅,傅海峰.东风4型机车牵引电机齿轮失效原因及解决措施[J].内燃机车,2000(2):38-39.

[2]Botha A.机车牵引电动机齿轮损坏研究与对策[J].徐陵,译.国外内燃机车,1994(7):38-44.

[3]胡友良,章易程.基于滑动的齿轮摩擦问题的研究[J].冶金矿山与建设,2002,34(2):24-26.

[4]章易程,田红旗.渐开线齿轮供油能力的研究[J].润滑与密封,2006(8):52-54.

[5]谢友柏.摩擦学设计主要是摩擦学系统的设计[J].中国机械工程,1999,10(9):968-973.

[6]刘峰壁.直齿圆柱齿轮磨损过程模拟[J].机械科学与技术,2004,23(1):55-59.

[7]Flodin A,Andersson S.Simulation of Mild Wear in Spur Gears[J].Wear,1997,207:16-23.

[8]Brauer J,Andersson S.Simulation of Wear in Gears with Flank Interference—a Mixed FE and Analytical Approach[J].Wear,2003,254:1216-1232.

[9]宋小欣.磨损齿轮啮合过程的动态模拟[J].西南交通大学学报,2001,36(4):392-395.

[10]格利布B B.数值法解摩擦学技术问题[M].孟献堂,译.北京:机械工业出版社,1989.

[11]章易程,李蔚,陈昭莲,等.渐开线外齿轮副相对滑动率的研究[J].机械设计,2001,18(7):27-29.

[12]章易程,李蔚,聂昌平.渐开线内齿轮副相对滑动率的研究[J].机械传动,2001,25(2):25-27.

[13]章易程,梅雪松,陶涛,等.直齿轮啮合弹性流体动力润滑的非稳态效应的研究[J].机械工程学报,2000,36(1):32-35.

[14]朱孝录,鄂中凯.齿轮承载能力分析[M].北京:高等教育出版社,1992.

[15]戚墅堰机车车辆厂.东风8B内燃机车[M].北京:中国铁道出版社,1999.

[16]Walton D,Goodwin A J.The Wear of Unlubricated Metallic Spur Gears[J].Wear,1998,222:103-113.

[17]王淑仁,闫玉涛,丁津原.渐开线直齿圆柱齿轮啮合磨损试验研究[J].东北大学学报(自然科学版),2004,25(4):146-149.