求解双线性单自由度复合随机系统

范么清, 楼梦麟

从而式(26)～(28)变为

非线性随机振动的分析方法有精确解析法、实用近似法和数值模拟法.数值模拟法以M onte Carlo法为代表.

从工程应用的角度来看,各种实用近似方法主要有等效线性化法[1-6]、随机有限元法[7-8]、构造M arkov 状态方程求解法[9]、半隐式积分法[10]、改进摄动法[11]等.其中,等效线性化法使用较多.

王国砚[1]提到两种等效线性化方法:方程差法和能量差法.M Grigoriu[12]用等效线性化法研究了由Levy 白噪声引起的随机系统的随机响应.S.H C randall[4]仔细研究了等效线性化方程差解法的两种程序.A ndrew W.Smyth 和Sami F.M asri[5]用等效线性化方法计算非平稳地震作用下线弹性弹簧系统的随机响应.Wing Kam Liu 等用随机有限元法[8]研究了内力为位移、速度、单元尺寸的非线性函数的非线性随机结构的求解方法.R.C.Micaletti[9]提出采用构造M arkov 状态方程求解随机反应.Yasuki Ohtori[9]提出采用半隐式积分法求解随机激励下有附加滞后阻尼的非线性结构的随机地震反应.

Nicola Impollonia 等[11]提出一种改进的摄动法,将随机量(包括随机质量、随机内力——阻尼力和回复力)分解成均值部分和变分部分,求解非线性随机结构的随机反应.

等效线性化法的等效方法很多,多用于非线性确定结构的随机反应求解.对于非线性复合随机系统,应用的不多.但非线性确定结构的随机反应求解方法仍然给复合随机系统的求解方法提供很多启发:首先,等效线性系统的等效参数与原非线性系统反应独立,这给等效参数的求解带来很多方便,按这种等效原则得到的随机反应具有一定的精确度;第二,在非线性很复杂的情况下,可以将阻尼项与恢复力项分别等效以便求解等效参数;第三,在假定非线性复合随机振动系统的反应概率分布类型时,不妨考虑反应概率分布类型为正态分布或均匀分布.

随机有限元法不涉及随机变量单独出现的式子,且方程右边荷载项已为确定性荷载,故能否转变为复合随机振动求解,似乎很困难.构造M arkov 状态方程的方法,是典型的复合随机微分方程的求解方法,但要求把通常给定随机激励的功率谱转变成白噪声过程的形式.半隐式积分法和构造M arkov状态方程求解法类似,如能熟练掌握由随机激励的功率谱转换为白噪声驱动的随机荷载,则也可利用构造M arkov 状态方程的方法直接求解非线性复合随机系统的反应.由改进摄动法的解题过程知,结构体系的反应可表示为关于独立随机变量的线性组合形式,如将激励表示为虚拟激励,就可采用改进摄动法求解非线性复合随机系统的随机反应.

虚拟激励法是林家浩1985 年提出的,以计算随机荷载作用确定结构的随机反应[13].虚拟激励法将线性结构的平稳随机反应功率谱分析转化为确定性的简谐反应分析.若设外部激励的功率谱为SFF(ω),可以将虚拟激励法的原理表述如下:

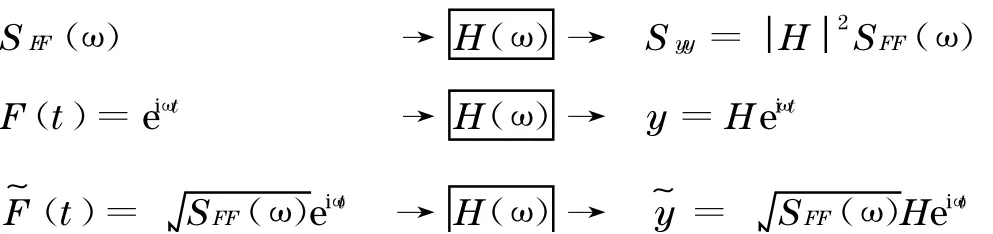
由上述虚拟反应的表达式可知,虚拟反应是时域和频域上的复数变量.文献[14]正是利用这一特点来直接消除1 阶随机反应的久期项.如果要完整地表述,显然要利用复数空间;如果要在实数空间中观察到虚拟反应,自然想到用复数的模.本研究仅仅关心结构的自振频率附近的虚拟反应,因此,取ω为结构自振频率时虚拟反应模的时程.

在上述分析的基础上,引入非线性改进随机摄动法,将双线性随机结构离散为均值部分和变分部分,并把随机激励按虚拟激励法展开,试着求解双线性随机结构在随机激励下的随机反应.

1 用非线性改进随机摄动法展开双线性随机结构

考虑一个单自由度双线性复合随机振动系统(图1)

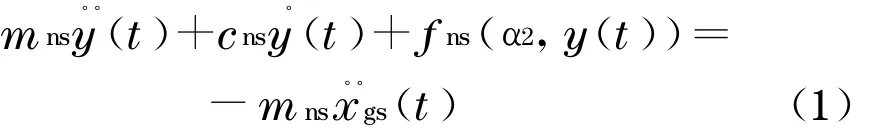
式中

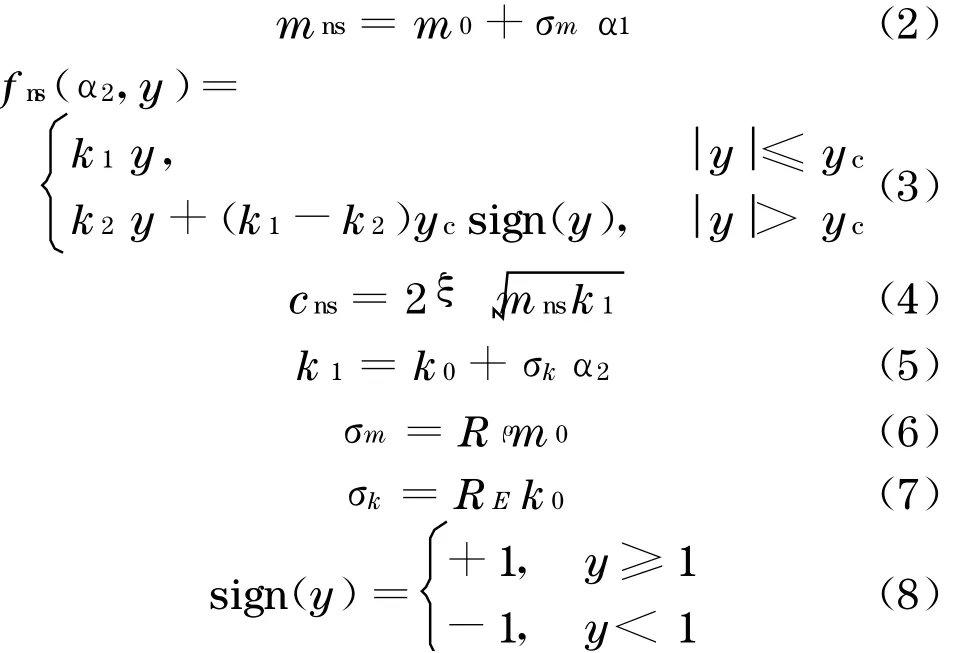
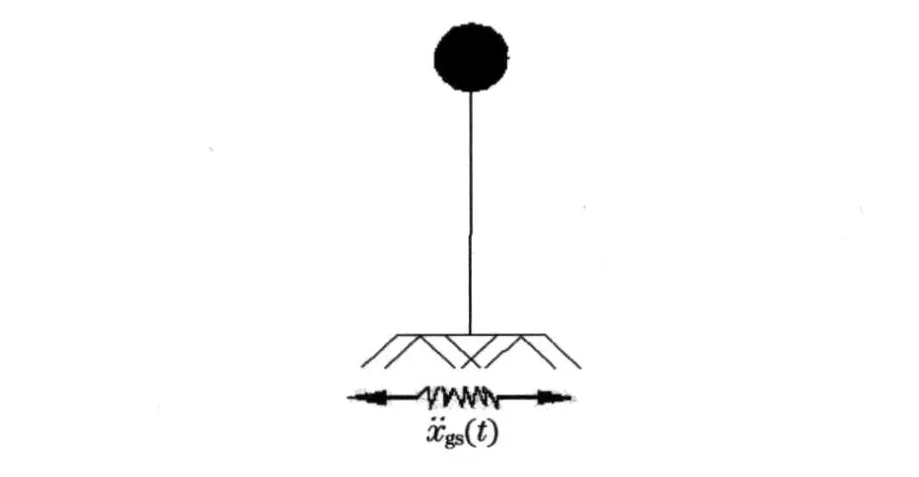
图1 单自由度系统力学模型Fig.1 Mechanical model of SDOF system

式(1)～(8)中:mns为随机质量;cns为随机阻尼;fns(α2,y)为非线性随机恢复力;kns为随机刚度;m0为随机质量均值;ξ为结构阻尼比;σm为随机质量均方差;α1,α2是均值为0、方差为1 的随机变量,此处采用高斯随机分布;k0为随机刚度k1的均值;σk为随机刚度均方差;Rρ,RE分别为密度、弹性模量的变异系数(此处假定随机弹性模量与随机密度相互独立);下标n和s分别表示非线性系统和随机系统,以区别于线性随机系统[14]分别为加速度、速度和位移随机反应为输入地震波随机过程;yc为双线性折线分界值.按非线性改进随机摄动法,将双线性随机结构展开如下:

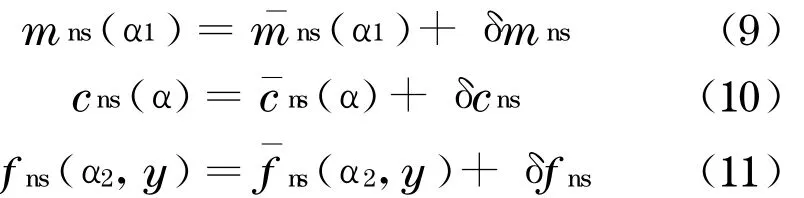
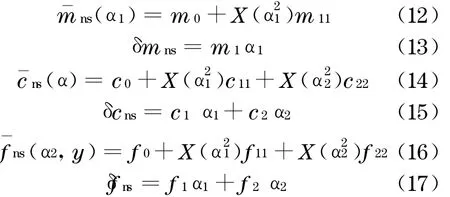
式中,X(·)表示随机参数的均值.其中,随机质量、随机阻尼各参数计算如下:

非线性随机回复力fns(α2,y)的各参数计算公式如下:

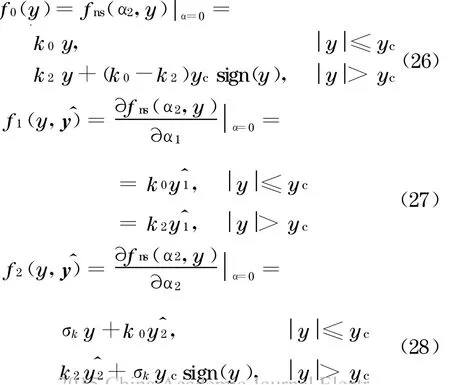
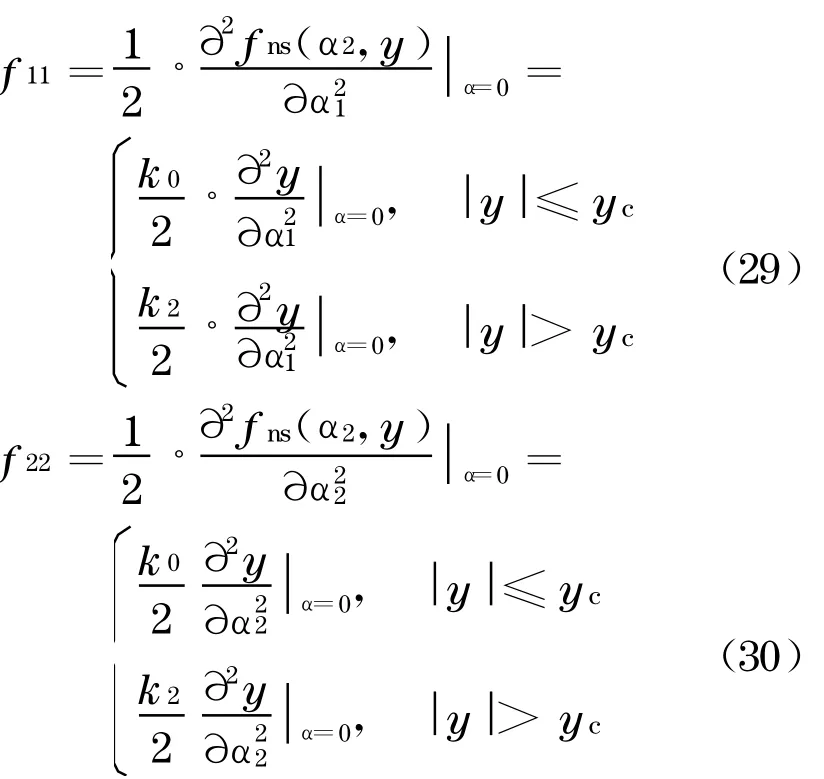
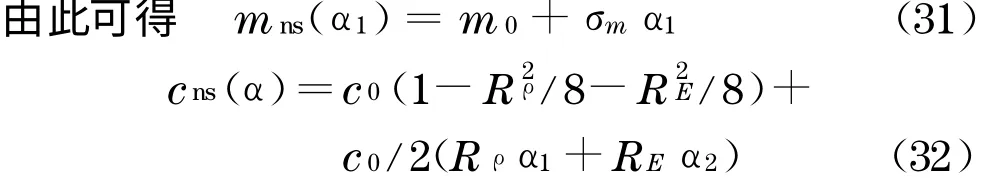
将随机反应写成反应均值及1 阶展开项,得

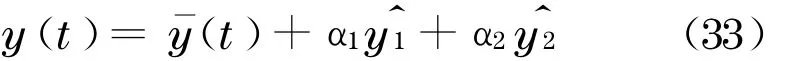
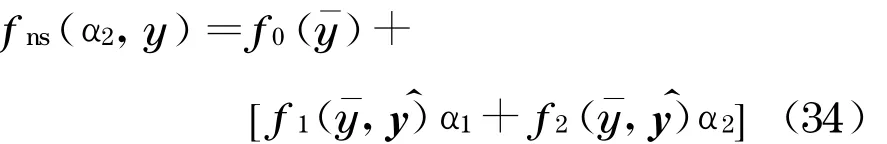
如果式(33)包含1 阶灵敏度的二次项,则f11≠0,f22≠0.将式(33)代入式(26)～(28),化简后可得

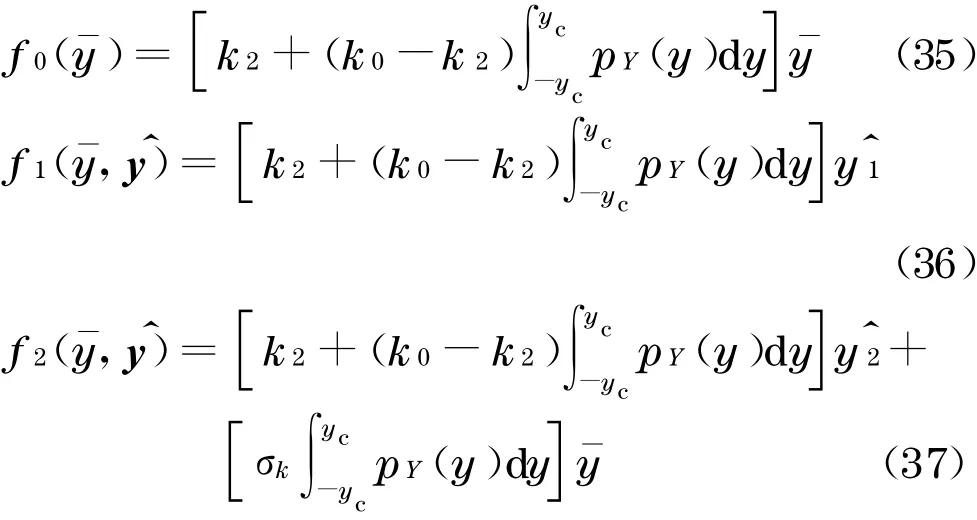
式中,复合随机系统随机反应的均值假定为零,但这一均值不同于

在文献[14]中,采用Monte Carlo模拟法模拟过这种双线性复合随机系统的随机反应,计算结果表明,随机反应的概率分布类型不是完全的正态分布,也不是均匀分布.其概率分布类型的离散程度较正态分布稍大,曲线稍缓和.本文参考文献[ 4] 的做法,考虑两种概率分布类型求非线性随机恢复力参数并形成虚拟摄动方程.

1.1 假定反应概率分布类型为正态分布

若反应服从正态分布,令

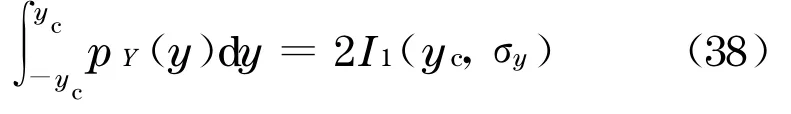
从而式(26)～(28)变为

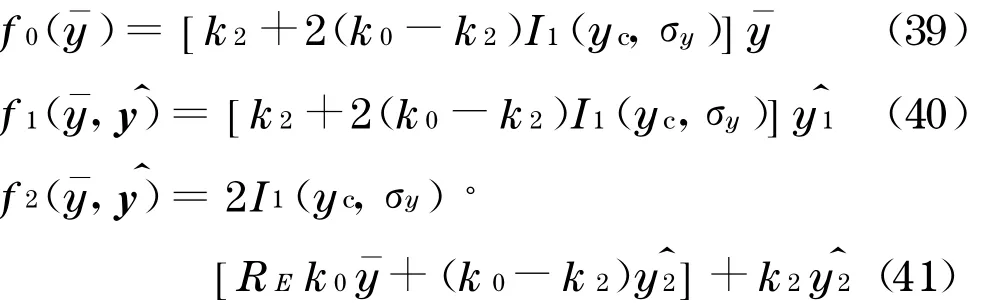
将式(39)～(41)代入式(34),可得

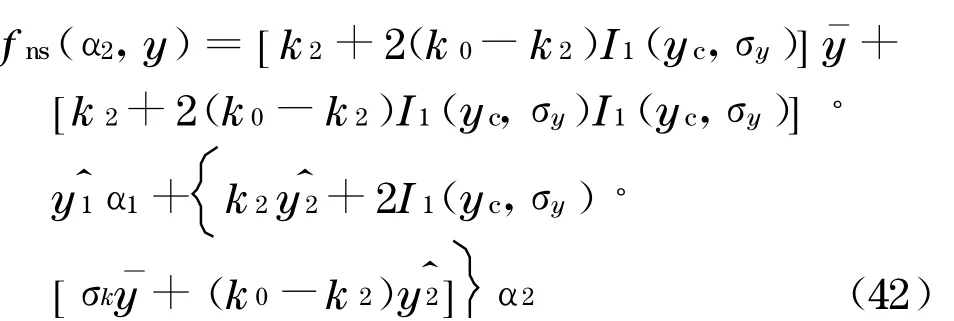
将式(31),(32),(42)代入式(1),按摄动法的思想,令式中随机参数前的系数相等,化简后可得

1.2 假定反应概率分布类型为均匀分布

若反应分布服从下式的均匀分布:

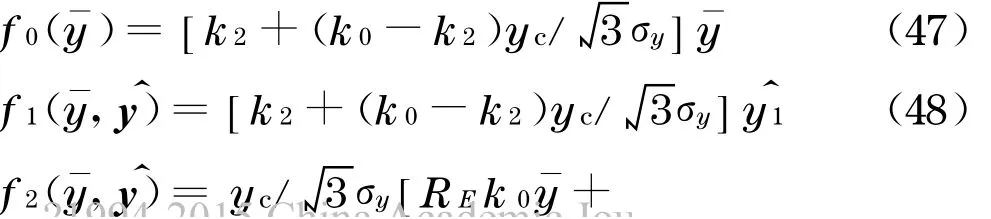
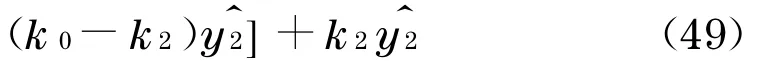
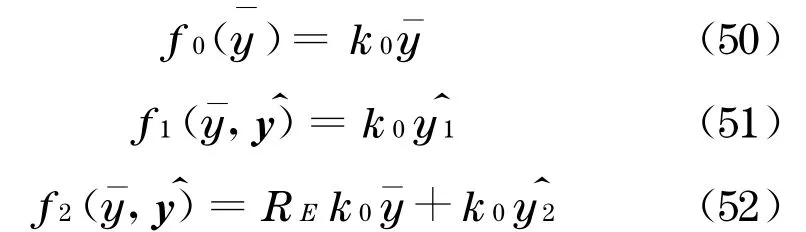
同理,将式(47)～(52)代入式(34),可求得随机恢复力,然后和随机阻尼、随机质量代入双线性随机微分方程,得各阶摄动方程.限于篇幅,此处不赘述.

2 用迭代方法求解展开后的随机微分方程

和线性复合随机振动系统类似,此处不考虑随机参数的交叉项及二次项.对比式(43)～(45)与线性单自由度复合随机系统的摄动展开公式[15],可以看到,由于同为摄动法,运动方程左边的常数项系数都是一样的,因此,这个方法也存在久期项的问题.非线性改进摄动法对于阻尼系数多了二阶项,当考虑k2=k0时,2I1(yc,σy)=1,双线性复合随机振动系统的摄动方程变为线性复合随机振动系统的摄动方程,双线性复合随机振动系统变为线性复合随机振动系统.因此,用于线性复合随机系统随机反应的求解方法,此处仍可采用.由于式(43)～(45)中,反应均方差未知,因此在每一时间步,采用迭代方法求解反应均方差,即先假定初始反应均方差,从而计算得到新的均方差,反复迭代直到反应均方差收敛,此时的均方差可作为下一时刻均方差值的初值.

3 计算结果比较

单自由度系统质点平均密度ρ0=2.5 ×103kg ·m-3,变异系数Rρ=5%,质点体积V=2 m3,弹性模量均值E0=1010Pa,变异系数R E=3%,截面惯性矩I=0.005 208 m4,杆件高度h=2 m.阻尼比ξ=0.05,质量m=ρV,刚度计算公式k=3EI/h3,屈服阶段的弹性模量为E0=3×109Pa.结构所受的地震作用为均匀调制非平稳随机地震作用,基岩与地面之间场地土的基频ωg=15.6 rad·s-1,基岩与地面之间场地土的阻尼比ξg=0.6,地面运动加速度峰值期望值峰值因子ν=3.阻尼的计算公式为c=2ξmk.均匀调制非平稳随机地震模型参数分别为λ1 =1.012 6,t1=1 s,t2=7 s,λ2=1.783 2,Te=10 s.假定反应概率分布类型为正态分布和均匀分布,分别求随机反应.

3.1 假定反应概率分布类型为正态分布时的计算结果

3.1.1 虚拟反应

图2 为假定反应概率分布类型为正态分布时,该非线性非平稳复合随机振动系统在65 rad·s-1处的虚拟反应(按虚拟激励法的原理,虚拟反应实际是一个复数量,这里用复数的模描述这个物理量).由图可见,由于非线性的影响,在反应的初始阶段和衰减阶段,虚拟反应变化剧烈,表现出很强的非平稳性.

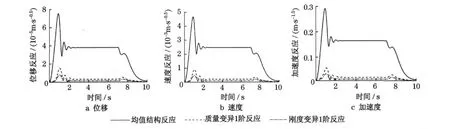
图2 虚拟反应(ω=65 rad·s-1)Fig.2 Pseudo response(ω=65 rad·s-1)

3.1.2 随机反应

图3 为计算得到的非线性复合随机振动系统的随机反应.图4 为位移反应的计算结果与Monte Carlo法模拟结果之间的相对误差.由图可知,在平稳阶段,相对误差近5%;速度和加速度反应的相对误差不大,平稳阶段时不到0.5%.在地震作用的非平稳阶段(包括地震作用初始增大阶段和衰减阶段),相对误差较大,但由于这时随机反应不大,二者差别也不大.

图5 为不同时刻的迭代次数,由图可知,最大迭代次数为5 次.

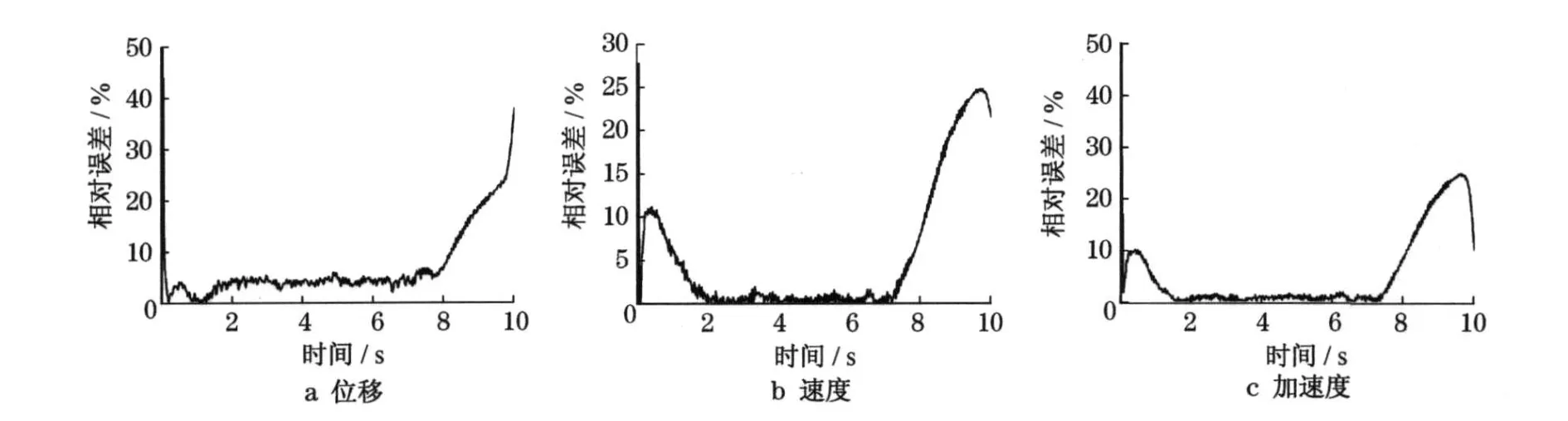
图4 非线性复合随机系统反应均方差相对误差(正态分布)Fig.4 Relative error of response mean variation about no-linear compound stochastic system(normal distribution)

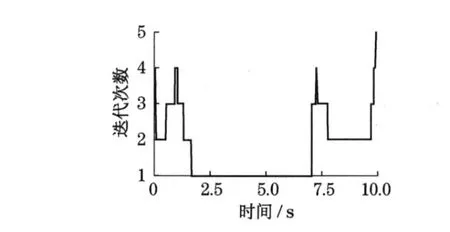
图5 迭代次数Fig.5 Iteration frequency

3.1.3 迭代计算精度的影响

图6 是迭代计算精度分别为0.1,0.05,0.01,0.001时得到的均方差反应.由图可见,计算时可以采用0.1 的相对误差.

3.2 假定反应概率分布类型为均匀分布

3.2.1 虚拟反应

图7 为假定反应概率分布类型为均匀分布时的非线性非平稳复合随机振动系统在65 rad·s-1处的虚拟反应.图7 与图2 的差别表现在平稳阶段的虚拟反应减小,地震作用增长阶段虚拟反应跳跃振荡更剧烈.

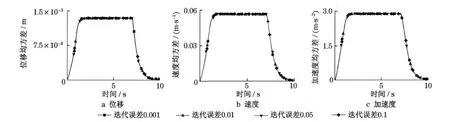
图6 不同迭代精度的反应结果比较Fig.6 Result comparison about different iteration precision

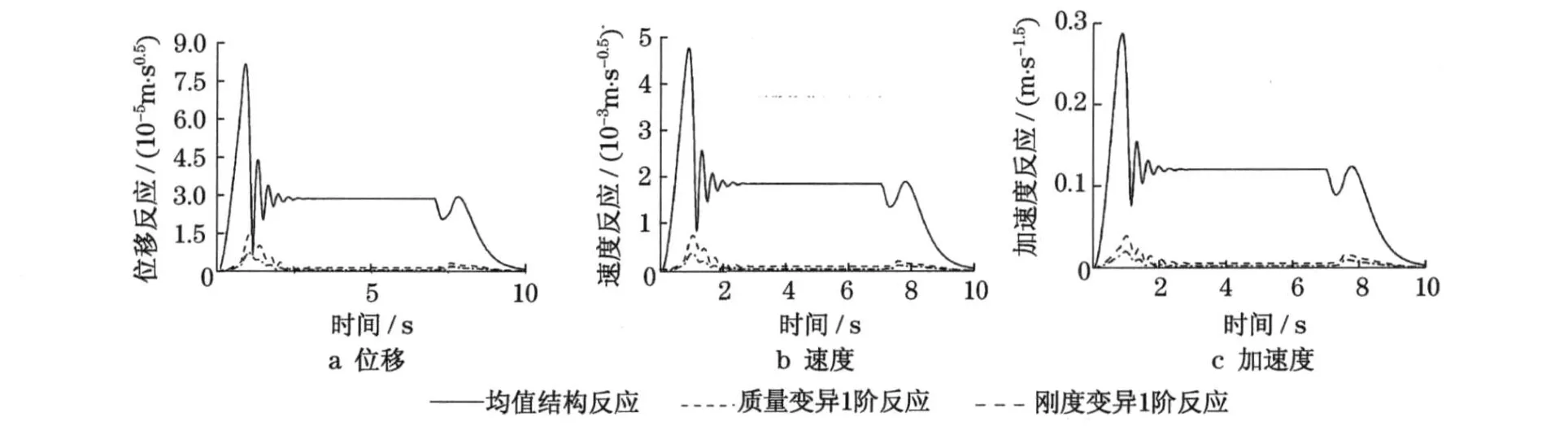
图7 虚拟反应(ω=65 rad·s-1)Fig.7 Pseudo response(ω=65 rad·s-1)

3.2.2 随机反应

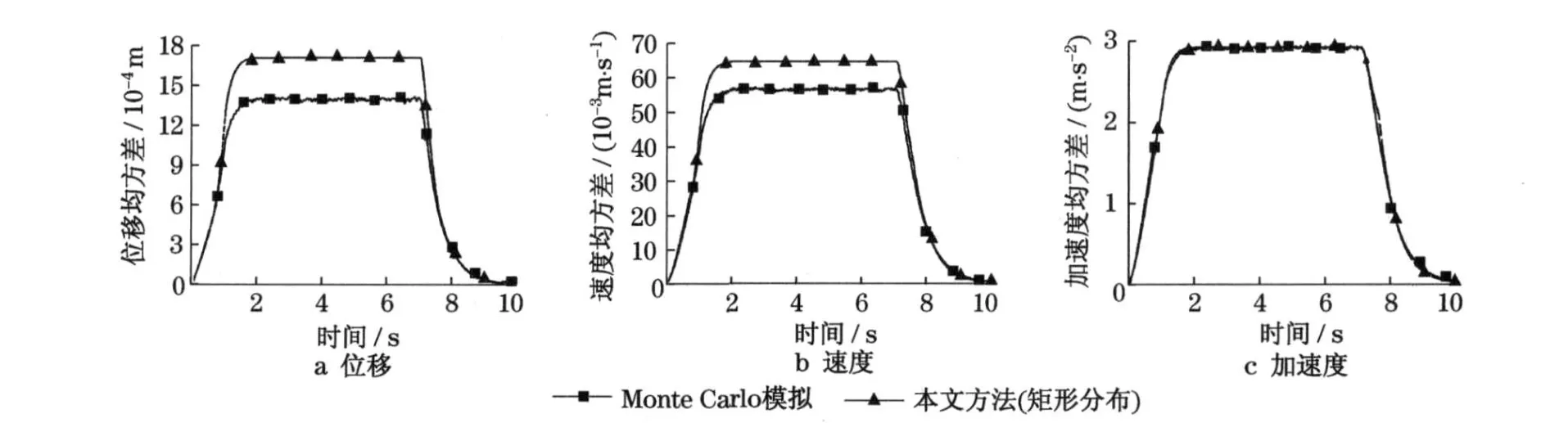
图8 非线性复合系统随机反应(均匀分布)Fig.8 Response mean variation about no-linear compound stochastic system(equal value distribution)

图8,9 分别为该非线性非平稳复合随机振动系统的均方差反应,以及相对于M onteCarlo模拟结果的相对误差.当假定反应的概率分布为均匀时,所算得平稳阶段的位移、速度均方差反应较M onte Carlo 模拟结果小,相对误差很大(15%～25%),加速度方差响应和Monte Carlo 模拟结果接近.非平稳阶段的相对误差依然很大.

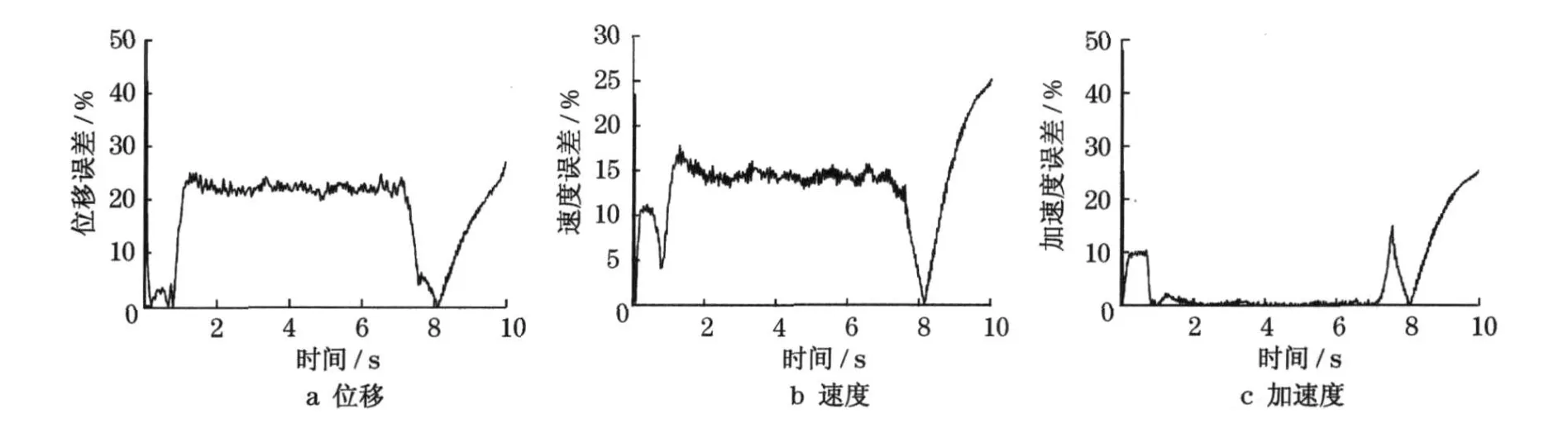
图9 非线性复合系统反应均方差相对误差(均匀分布)Fig.9 Relative error of response mean variation about no-linear compound stochastic system(equal value distribution)

图10 为不同时刻的迭代次数,由图可知,最大迭代次数为5 次.

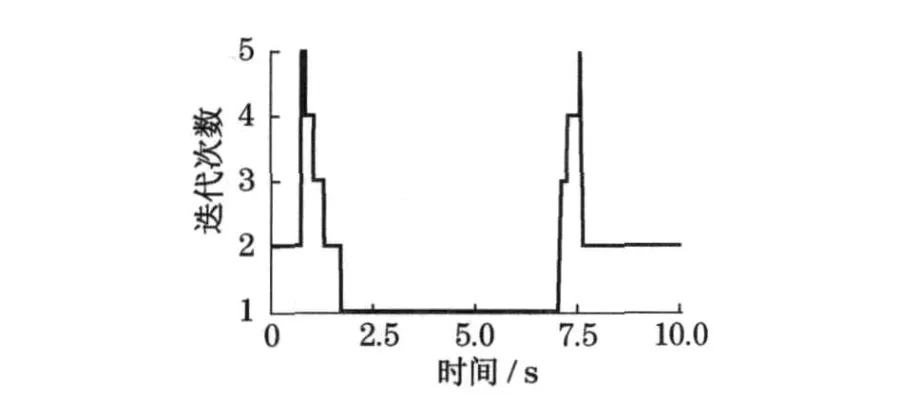
图10 迭代次数Fig.10 Iteration frequency

4 误差原因及需要进一步研究的问题

本文将非线性改进摄动法与虚拟激励法结合,求解了双线性复合随机系统的随机反应.计算结果与Monte Carlo 模拟结果[15]有误差,这些误差产生的原因有如下几点:

(1)随机反应的展开为1 阶展开.由于是单自由系统,计算结果与模拟结果误差不是很大;但当用于多自由度系统时,误差可能会大.

(2)对随机反应概率分布类型的假定.本文假定概率分布类型为正态分布与均匀分布,计算结果表明,不同概率分布类型的计算误差是不一样的.Monte Carlo 模拟结果表明,平稳阶段反应概率分布类型不是完全正态分布,而是比对应正态分布的离散程度稍大,曲线稍平缓.

因此,还需要在以下方面展开:①将本方法用于多自由度系统;②进一步探讨其他非线性情况;③对不同反应概率类型进行比较.

5 结论

与等效随机线性化法[15]相比,按非线性改进摄动虚拟激励法求解随机反应,更容易收敛.等效随机线性化法的计算精度不是很好,而改进随机摄动法的计算精度要好些.但改进随机摄动法也存在久期项问题.反应的概率分布类型也影响计算精度.

双线性非平稳复合随机振动系统的随机反应有一些特点:频域虚拟反应在非平稳增长阶段跳跃性很大,表现较强的非平稳性;地震作用增长和衰减的非平稳阶段相对误差很大,但此时的反应很小,不影响计算结果;当假定反应概率分布类型为均匀分布时,平稳阶段的均方差相对误差较大.

[ 1] 王国砚.非线性随机振动中的等效线性化方法研究及在工程的应用[ D] .上海:同济大学航空航天与力学学院, .1999.WANG Guoyan.Study on equivalent linearization m ethods for non-linear stochastic vibration and their applications in Engineering [ D] .Shanghai:Tongji University.College of Aerospace Engineering and Applied M echanics,1999.

[ 2] Naess A.Prediction of extreme response of nonlinear structures by extended stochastic linearization[ J] .J Pro Eng ng Mech,1995(10):153.

[ 3] Pol D Spanos,Spy ro Tsavachidis.Deterministic and stochastic analyses of a nonlinear system w ith a Biot visco-elastic element[ J] .J Earthquake E ngng Struct Dyn,2001,30:595.

[ 4] C randall S H.Is stochastic equivalent linearization a subtly flawed procedure?[ J] .J P robabilistic Engineering Mechanics,2001,16:169.

[ 5] Andrew W Smy th, Sami F M asri.Non-stationary response of nonlinear sy stems using equivalent linearization with a com pact analytical form of the ex citation process[ J] .J Probabilistic E ngineering Mechanics,2002,17:97.

[ 6] Proppe C, P radlw arter H J, Schueller G I.Equivalent linearization and Monte C arlo simulation in stochastic dynamics[ J] .J Probabilistic Engineering Mechanics, 2003,18:1.

[ 7] Koyluoglu H U, Nielsen S R K, Cakmak A S.Solution of random structural system subject to non-stationary excitation: transforming the equation w ith random coefficients to one with deterministic coefficients and random initial conditions [ J] .J Soil Dynamics and Earthquake E ngineering,1995,14:219.

[ 8] LI U Wingkam,Ted Bel Ytschko M ani.A probabilistic finite elem ents for nonlinear structural dynamics[ J] .J Computer Methods in Applied M echanics and Engineering,1986,56:61.

[ 9] Micaletti R C,C akm ak A S, Nielsen S R K,et al.A solution method for linear and geom etrically nonlinear MDOF systems w ith random properties subject to random excitation[ J] .J Pro E ngng M ech,1998,13(2):85.

[10] Yasuki Ohtori,Billie F Spencer Jr., M ASCE.Semi-im plicit integration algorithm for stochastic analysis of multi-deg reeof-freedom structures[ J] .J Eng Mec,2002,128(6):635.

[ 11] Nicola Im pollonia, Giuseppe Muscolino.Static and dynamic analy sis of non-linear uncertain structures[ J] .J Meccanica,2002,37:179.

[ 12] Grigoriu M .Equivalent linearization for sy stems driven by Levy White noise[ J] .J Probabilistic Engineering Mechanics,2000,15:185.

[ 13] 林家浩,张亚辉.随机振动的虚拟激励法[ M] .北京:科学出版社,2004.LIN Jiahao, ZHANG Yahui.Pseudo excitation m ethod of stochastic vibration[ M] .Beijing:Science Press,2004.

[ 14] 范么清,楼梦麟,毛巍.非线性单自由度复合随机振动的蒙特卡罗模拟[ J] .武汉理工大学学报,2008,30(1):67.FAN Yaoqing, LOU M englin, M AO Wei.Monte Carlo simulation on stochastic response of SDOF double stochastic vibration sy stem with nonlinear m aterial[ J] .Journal of Wuhan University of T echnology,2008,30(1):67.

[ 15] 范么清.非线性复合随机振动方法研究及其工程应用[ D] .上海:同济大学土木工程学院,2007.FAN Yaoqing.Study on methods for non-linear compound stochastic vibration and their applications in Engineering[ D] .Shanghai: Tongji University. College of Civil Engineering,2007.