地铁振动荷载下隧道周围加固软粘土分形研究

唐益群,王元东,李仁杰,赵 化

近年来,分形理论成为探索物质组成复杂性的有效方法,并开始在土体物质组成及其关系的定量研究方面应用.土体结构具有分形特征,这一论断已经被广泛接受.在国外,一些学者在土体微观结构的分形研究方面已经取得了很多的成果[1-4],而国内近些年来也取得了可喜的成绩,并尝试将这些成果应用于实际工程中.徐永福、史春乐通过研究发现土粒分布是分形的,且各种土粒分布的分维介于2 ～3,并且运用土孔隙分布的分维确定水分特征曲线[5].王宝军、施斌等通过对膨胀土土样微观结构图像分析,论证了粘性土微观结构的分形特征,并分析了分形维数与土体微观结构类型之间的关系[6].唐益群等利用压汞仪微观试验研究方法,对隧道周围饱和软粘土微结构进行定量研究.结果表明,孔隙分形维数在隧道不同深度的变化规律可以用不同的循环应力比(CSR)来体现[7].刘莹、王清等应用分形几何理论对地基处理中地表沉降和孔隙水压力进行了分形几何研究,发现二者具有多层次的分形几何特征,结合实际工程,确定了划分界限,并建立了分维数与固结度、分维数与沉降量的相关关系曲线[8].周翠英等从室内固结试验和三轴固结试验出发,研究不同荷载条件下软土微观结构变化与固结变形特征,并运用图像处理技术,提取微观结构参数,分析微观结构参数与荷载、变形和强度之间的关系,建立了基于微观结构的软土沉降计算模型,并将这一模型应用于实际工程中[9].陈慧娥、王清等研究发现,水泥加固土颗粒分布分形的计盒维数与其强度呈一定的相关性[10].因此,选择一个合适的参量把土试样微观结构特征的变化与试样的宏观力学特征联系起来,将有助于进一步了解和认识土体的变形特性,从而为实际工程提供一定的理论依据.

笔者通过对上海地铁4 号线海伦路站加固软粘土在不同荷载条件下的循环三轴试验和压汞测试,对比分析加固软粘土振动前后的分形维数,并探讨加固软粘土微观结构参数(分形维数)变化与荷载形式的关系及其对残余应变的影响,得到了一些有益的结论.

1 试验方法

首先,将取得的加固软粘土做室内循环三轴试验,然后进行压汞测试.下面详细介绍各试验过程及参数.

1.1 室内循环三轴试验

试验采用英国进口多功能动态循环三轴试验系统GDS(global digital systems).GDS 可以实时监控整个试验过程,高速采集并储存数据,具有精度高、操作简易、结果可靠等优点, 是一套数字化试验设备.

原状饱和软粘土在天然应力条件下,应力状态处于K0(正常固结条件下的固结比)固结应力条件.在遭受地铁行车荷载作用时,其幅值及频率很少有相关的研究.张曦、唐益群等通过现场连续监测,采集到大量的钻孔实测数据[11],通过对钻孔实测数据的汇总、分析、整理,得到地铁列车经过监测点时土体的响应频率有2 个:高频fH一般为2.4 ∶2.6 Hz,低频fL一般为0.4 ∶0.6 Hz.考虑到加固后土体响应频率有可能变化,室内试验采用3 个频率,分别为0.5,1.5,2.5 Hz.

在循环试验中,首先对圆柱形土样进行反压饱和,反压的作用是促使土样在固结过程中尽快饱和,取值100 kPa.为了最大限度地模拟现场条件,试样在K0条件下固结,根据土样本身的物理力学指标及工程实际经验,取K0=0.7.围压σh是根据实际天然土层计算所得,即σh=K0σv(σv=∑γihi).固结完成后开始循环三轴试验;循环应力σd的施加应能最大限度模拟土体可能承受的动荷载,考虑到列车及隧道体系施加给隧道底部的附加应力在20 ～40 kPa[12],即30±10 kPa,试验采用的荷载幅值分别为20,30,40 kPa.循环荷载以半波峰幅值施加于土样上.以上各参数均以现场实际数据为依据.

相关资料显示[7,11],地铁通过时,地铁振动荷载传至隧道周围土体引起的动力响应是周而复始的循环响应,因此,试验时采用应力控制式循环加载模块.试验方案如表1 所示.

1.2 压汞试验

试验采用美国生产的A U TOSCAN 60 型自动压汞仪.对室内循环三轴试验前后的不同土样进行取样、切取、冷冻干燥脱水以备试验所用.试验时,在真空条件下将汞注入样品管中,然后进行低压和高压分析,最高压力达到400 M Pa.

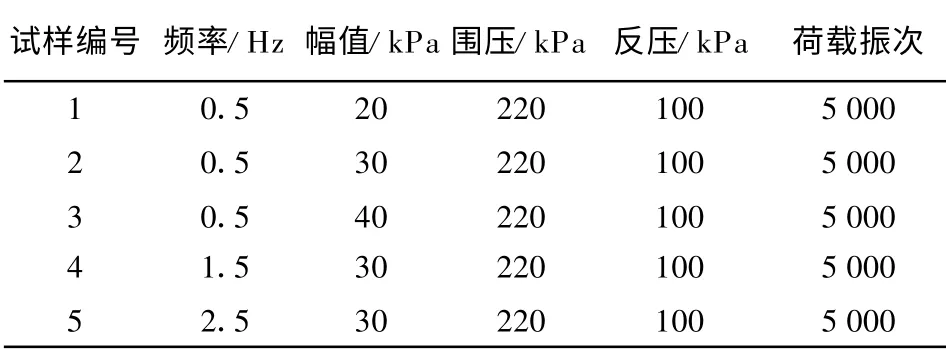
表1 不排水动态循环三轴试验方案及控制参数Tab.1 Scheme of undrained dynamic cyclic triaxial test and control parameters

汞是液态金属,不仅具有导电性能,而且还具有液体的表面张力.正因为具有这些特性,在压汞过程中,随着压力的升高,汞被压至样品的孔隙中,所产生的电信号通过传感器输入计算机进行数据处理,模拟出相关图谱,从而计算出孔隙度及比表面积等数据.

用于压汞试验的,除了上述循环三轴试验之后的试样以外,另增加了未进行循环三轴试验的加固软粘土试样(编号6).

2 分形模型与分维计算

2.1 分形模型

表征孔隙特性的分形模型主要有Menger 海绵模型和基于热力学关系的分形模型.

2.1.1 M enger 海绵模型

考虑边长为1 m 的一个立方体,将边长均分为b等分,可得到b3个边长为1/b的小立方体,将用区间[1 ∶b3]内不重复的随机整数对每个小立方体编号.按以下操作规则去掉一部分小立方体:设每次操作时,孔出现的概率均为P(0 ＜P＜1),取整数m=[(b3-Pb3)] .对于b3个小立方体,若随机整数编号大于m,则去掉该立方体,否则就保留.以上述规则重复构造下去,不断地减小剩余实心立方体的尺寸,直到规定的迭代操作次数为止.操作完成后,空心部分即代表多孔介质的孔隙结构,实心部分即为多孔介质的骨架结构.采用上述规则产生的多孔介质模型称为Menger 随机海绵模型[13].

2.1.2 基于热力学关系的分形模型

采用压汞法测量多孔物料孔隙体积与孔径的关系时,外界环境对汞所作的功等于进入孔隙内汞液的表面能增量,所施加于汞的压力p(kPa)和进汞量V(m3)满足一定的关系式[14].通过量纲分析,可将多孔物料孔隙表面积S(m2)的分形标度与孔隙孔径r(m)和进汞量V进行关联,得到孔隙分形维数Dt的表达式式中:为第i次进汞操作的进汞量;n为在进汞操作中施加压力的间隔数;rn为第n次进汞所对应的孔隙半径;V n为压力间隔1 ～n时的累计进汞量;C1为常数.

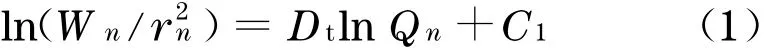
以lnQn为横坐标为纵坐标,所得到直线的斜率即为分形维数Dt.

2.2 分维计算

分形维数反映了构成孔隙曲面的弯曲复杂程度,维数越大,表明物料孔隙表面在空间的形貌特性偏离光滑表面的程度越远, 孔隙结构的复杂程度越高[15].

文献[7]指出,饱和软粘土的孔隙分维不能很好地满足M enger 随机海绵模型,而采用基于热力学关系的分维模型计算则呈现出合理的分形维数.热力学关系的分维模型计算方法关联了压汞过程的施加压力p和进汞量V,并间接反映了进汞过程中所对应的孔隙半径及数量变化,是对微观结构参数(孔径及其数量)变化特征的量化反映.

值得说明的是,在分形曲线中,会出现明显的非直线段,所以直线段的选取(分形区间)至关重要.不同数据段的分形维数可能差别很大,所以,这里选取试验整个进汞过程中得到的数据(进汞压力、孔隙半径、进汞量)做计算.图1 为采用基于热力学关系的分形模型计算加固软粘土的分形维数.

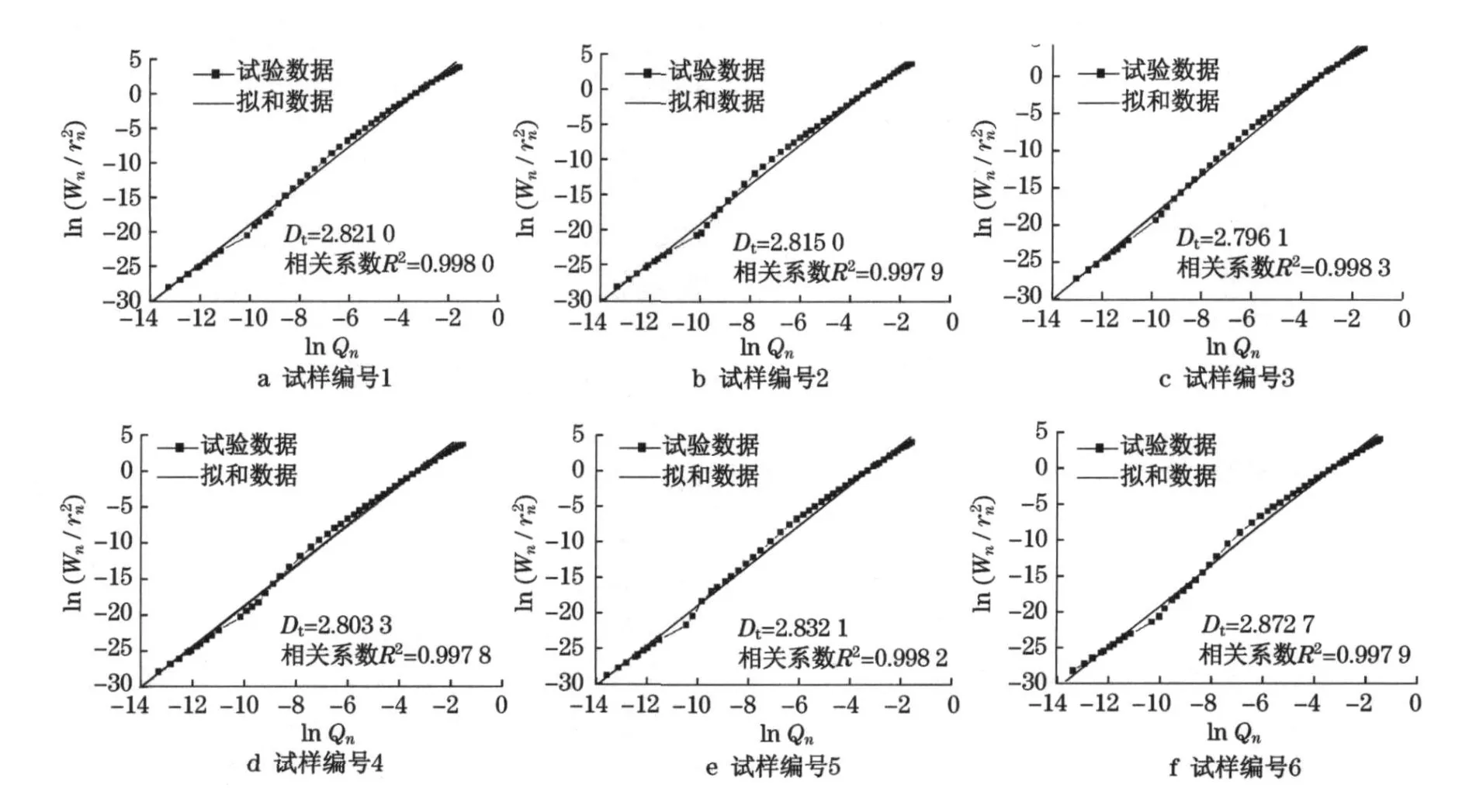
图1 分形维数计算图Fig.1 Fractal dimension calculated through the model of thermodynamics correlation

由图1a,b,c,d,e,f 可以看出,加固软粘土的压汞试验数据与lnQn相关系数均在0.99以上,呈显著的线性关系,拟合直线的斜率即为分形维数Dt.所得分形维数计算结果列于表2 中.

3 结果与分析

3.1 研究结果

从表2 可见,加固后的试样的分形维数大约为2.75 ～2.90.将热力学关系模型的分形维数Dt与振动频率及振动荷载幅值的关系进行整理,分别得到图2a,b.由图可见,其他条件相同时,Dt随荷载频率的增大而增大,随荷载幅值的增大而减小.

表2 热力学关系模型分形维数计算表Tab.2 Fractal dimensions calculated through the model of thermodynamics correlation

图2 分形维数D t与循环荷载Fig.2 Relationship between fractal dimensions and cyclic loading amplitudes

将残余应变εp与振动次数N的关系进行整理(如图3 所示).从图3 可以看出,在荷载施加初始阶段(较小的振次下),残余应变迅速产生并急剧增加,残余应变的增长速率随着振次的增加衰减很快.经过一个衰减的过渡阶段之后,残余应变随着振次的增加几乎不再上升.相同频率下,相同振次时的残余应变随着荷载幅值的增大而增大;相同荷载幅值下,相同振次时产生的残余应变随着荷载频率的增大而减小.频率越小,荷载幅值越大,残余应变达到稳定值的振动次数越大.

将分形维数与振动后残余应变的关系整理,得到图4.从图4 可见,残余应变随分形维数的增大总体上呈减小趋势.可以用多项式拟和,其方程为

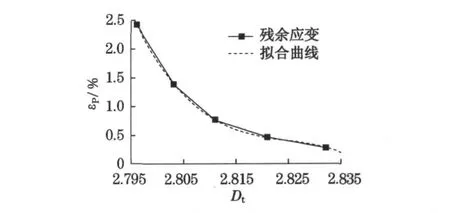
图4 残余应变与分形维数关系Fig.4 Relationship between fractal dimensions and residual strain

3.2 机理分析

试验和实践均表明,在注浆开始时,浆液总是先充填较大的空隙(这种现象在填土层中尤为明显),然后在一定的压力下渗入土体孔隙.浆液对四周土体产生挤压,先充填、渗流,后劈裂,使浆液沿着裂缝向周围土体扩散.注入相当可观的浆液后,加固后的土层常呈一层层薄片状.

随着振动次数的增加,土结构单元有压密的趋势,相邻且相互重叠的两个或多个单元之间逐渐靠近、压密,孔隙变得有定向性和规律性.试验表明,其他条件相同时,频率越低,幅值越大,振动对其影响越大.表现为相同的加荷周数内,孔压越大,产生较大的变形量,并具有较大的软化指数,孔隙变得越有定向性和规律性,所以分形维数越小.与传统意义上的理解似乎不符的是,低频产生较大的变形量,具有较小的分行维数.这是因为频率越低,意味着荷载变化越慢,相同的荷载作用次数下,低频荷载作用时间长,更有利于土体的压密.所以实际上并不矛盾.

这种频率越低、荷载幅值越大、应变越大的现象是不难解释的.在地铁行车荷载作用和隧道周围土体变形的过程中,地铁运行时的动能一部分通过铁轨及隧道结构转移到土体上.这部分动能消耗于抵消土体内部的等量颗粒骨架结构能,这样,土体内部的能量平衡被打破,继而形变.转移的地铁行车动能越多,隧道周围土体的形变就越大.而在相同振动次数作用下,荷载振动频率越低,意味着荷载变化越慢,荷载作用在土体上的总时间越多.荷载振动幅值越大,表明总能量越大,转移到土体上的动能也就越多,因此,土体能够产生更大的形变.

基于上述分析可知,在地铁运营相当长的一段时间内,地铁隧道周围土体会存在结构单元之间的压密过程,表现为长期附加沉降的增加.为避免过大的长期附加沉降,对临界边界范围内的土体加固处理是必要的,并需采取一定的隔振措施,将传递到土体的荷载控制在一定范围内,以减小地铁运营荷载对周围土体的影响.

4 结论

(1)其他条件相同时,加固软粘土的分形维数随振动频率的增大而增大,表现为低频更有利于土体的压密.

(2)其他条件相同时,加固软粘土的分形维数随振动荷载幅值的增大而减小,表现为荷载越大,变形量越大.

(3)残余应变随分形维数的增大呈总体减小的规律,并且能够较好地用三次多项式拟合.

[ 1] LUIS E Vallejo.Fractal analysis of the fabric changes in a consolidating clay[ J] .Engineering Geology,1996,43:281.

[ 2] Millaa H, Gonzaalez-Posad M .M odelling soil w ater retention scaling Comparison of a classical fractal model with a piecew ise approach[ J] .Geoderma1,2005,125(1～2):25.

[ 3] Jody R Gibson, Henry Lin,Mary Ann Bruns.A comparison of fractal analy tical methods on 2-and 3-dimensional Computed tomographic scans of soil agg regates[ J] .Geoderma,2006, 134(3～4):335.

[ 4] Prosperini N, Perugini D.Particle size distributions of some soils from the Um bria Region(Italy):fractal analysis and numerical m odelling[ J] .Geoderm a1,2008,145(1～2):185.

[ 5] 徐永福,史春乐.用土的分形结构确定土的水分特征曲线[ J] .岩土力学,1997,6(2):40.XU Yongfu, SH I Chunle.Calculation of soil-w ater characteristic curves by using fractal structure of soil[ J] .Rock and Soil Mechanics,1997,18(2):40.

[ 6] 王宝军,施斌,刘志彬,等.基于GIS 的粘性土微观结构的分形研究[ J] .岩土工程学报,2004,26(2):244.WANG Baojun,SH I Bin, LIU Zhibin,et al.Fractal study on microstructure of clayey soil by GIS[ J] .Chinese Journal of Geotechnical Engineering,2004,26(2):244.

[ 7] 唐益群,张曦,赵书凯,等.地铁振动荷载作用下隧道周围饱和软黏土分形研究[ J] .土木工程学报,2007,44(11):86.TANG Yiqun, ZHANG Xi, ZHAO Shukai, et al.A study on the fractals of saturated soft clay sur rounding subw ay tunnels under dynamic loads[ J] .China Civil Engineering Journal,2007,44(11):86.

[ 8] 刘莹,王清.地基处理中孔隙水压力及地表沉降的分形特征[ J] .长春科技大学学报,2001,31(3):294.LI U Ying,WANG Qing.The fractal characteristics analysis of pore w ater pressure and g round-surface settlement in soil treatment[ J] .Journal of Changchun University of Science and Technology,2001,31(3):294.

[ 9] 周翠英,林春秀.基于微观结构的软土变形计算模型[ J] .中山大学学报:自然科学版,2008,47(1):17.ZHO U Cuiying, LIN Chunxiu.Research on deformation calculation model of soft soil based on microstructure[ J] .Acta Scientiarum Naturalium Universitatis Sunyatseni, 2008, 47(1):17.

[ 10] 陈慧娥,王清.水泥加固土微观结构的分形[ J] .哈尔工业大学学报,2008,40(2):307.C HEN Huie,WANG Qing.Fractal study on microstructure of cement consolidated soil[ J] .Journal of Harbin Institute of Technology,2008,40(2):307.

[ 11] 张曦,唐益群,周念清,等.地铁振动荷载作用下隧道周围饱和软粘土动力响应研究[ J] .土木工程学报,2007,40(2):85.ZH ANG Xi, T ANG Yiqun, ZH OU Nianqing, et al.Dynamic response of saturated soft clay around a subw ay tunnel under vibration load[ J] .China Civil Engineering Journal, 2007, 40(2):85.

[ 12] 刘沙.地铁行车荷载作用下隧道周围饱和软粘土流变效应研究[ D] .上海:同济大学地下建筑与工程系,2007.LI U Sha.T he Study on the rheological properties of saturated soft clay around the tunnel under subw ay loading [ D] .Shang hai:Tongji Unibersity.Department of Geotechnical Engineering,2007.

[ 13] Coppens M O, Froment G F.Diffusion and reaction in a fractal catalyst pore-Ⅱdiffusion and first order reaction[ J] .C hemical Engineering Science,1995,50(6):1027.

[ 14] ZH ANG Baoquan,LI Shaofen.Determination of surface fractal dimension for porous media by mercury porosimertry[ J] .Ind Eng Chem Res,1995,34:1383.

[ 15] 刘永忠,陈三强,孙皓.冻干物料孔隙特性表征的分形模型与分形维数[ J] .农业工程学报,2004,20(6):41.LI U Yongzhong, CH EN Sanqiang, SUN Hao.Characterizing pores in freeze-dried materials by fractal models and fractal dimensions[ J] .T ransactions of the Chinese Society of Agricultural Engineering,2004,20(6):41.