基于物理机制的风力发电高塔系统风场模拟

贺广零,李 杰

(同济大学 建筑工程系,上海200092)

随机风场作用下结构的响应以及动力可靠度是工程界普遍关心的问题.为了分析结构的时域风振响应,需要通过风场模拟,生成具有结构所在场地风荷载统计特性的样本函数.研究现有的风场模拟方法(如谐波合成[1-2]、线性滤波器[3-4]和小波分析[5-6]等),不难发现,这些方法都基于功率谱密度函数.而在本质上,功率谱密度函数(包括自谱和互谱)是对平稳随机过程的数值特征描述,很难反映本源随机过程的丰富概率信息,由此也导致了对结构进行精细化随机振动反应分析的困难[7].事实上,即使是平稳过程,仅依据数值特征解答也很难获得结构动力可靠度的精确解答.近期,李杰和张琳琳从随机函数的角度出发研究随机过程,将脉动风速时程样本经Fourier 变换得到的Fourier 谱视为随机函数,提出了随机Fourier 谱的概念, 获得了随机Fourier 幅值谱经验物理公式,从而探索了一条从物理本质上反映随机过程的新道路[8].在随机Fourier谱的基础上,贺广零和李杰针对风力发电高塔系统,提出了考虑桨叶旋转效应的旋转Fourier 物理谱[9].在此基础上,笔者首先提出了基于物理机制的旋转Fourier 互谱,有效地考虑了桨叶旋转效应和桨叶上不同点风速之间的相关性.结合典型的1.25 MW 三桨叶变桨距风力发电高塔系统,对旋转Fourier 谱(随机Fourier 谱)进行逆Fourier 变换,生成了作用于桨叶(塔体)的风速时程.

1 旋转Fourier 谱物理机制

空间中一点的风速,可以用一个标准的随机过程描述.对于体量较大的结构,需要反映不同位置风速之间的相互关系,此时空间的风速是一个时变的随机场.对于时变随机场,空间中任意一点的风速不仅与该点的空间位置坐标有关,而且与时间有关.

为了准确描述作用在旋转桨叶上的风速时程,可有规律地在风轮平面取样(图1).假设在同一半径r上取N个样本点,并将风轮平面上l1点风速时程中零时刻的风速……l i点风速时程中(i-1)Δt时刻风速,l i+1点风速时程中iΔ 时刻风速……l N点风速时程中(N-1)Δt时刻的风速提取出来,按照时间顺序组合成一组新的风速时程,对其进行Fourier 变换即可得到旋转Fourier 谱.在本质上,旋转Fourier 谱由作用在桨叶上的风速经过Fourier 变换而来,是一种自身蕴含了桨叶旋转效应的紊流风速谱.因此,基于该谱进行风力发电高塔系统风振动力响应分析时,无须再次考虑桨叶旋转效应.

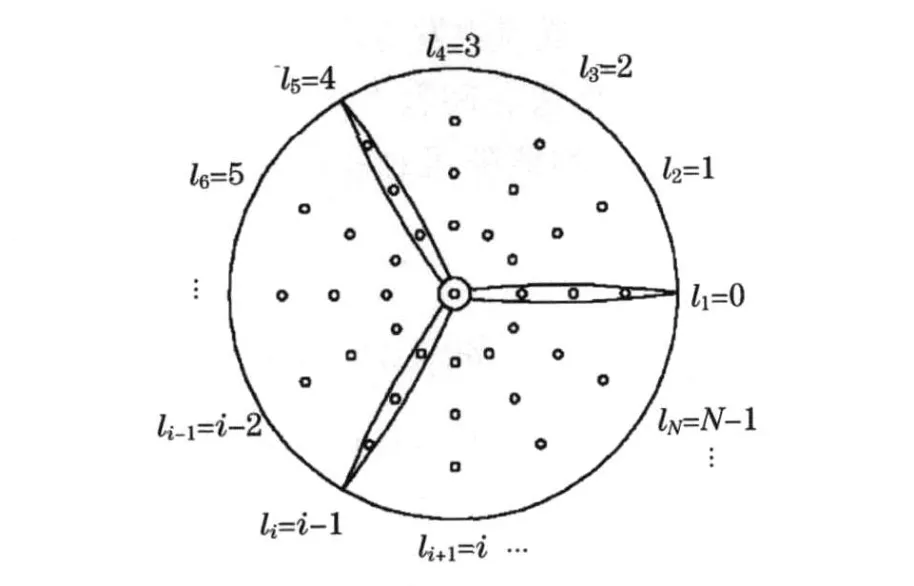
图1 风轮平面上取样点位置Fig.1 Sample points in the rotor plane

2 旋转Fourier 互谱模型

桨叶上2 点处脉动风速的旋转Fourier 互谱,与塔体上2 点处脉动风速的随机Fourier 互谱有本质的不同.主要体现在两个方面:①由于桨叶的旋转效应,旋转Fourier 互谱必须在旋转坐标系下考虑2点处脉动风速的相关性.在旋转坐标系下,2 点处脉动风速的互谱已经不能简单地通过各点处脉动风速的自谱与相干函数的乘积来确定.②旋转Fourier互谱体现在桨叶(而非风轮平面)上任意2 点处脉动风速之间的相关性.因此,旋转Fourier 互谱可分为同一桨叶上2 点之间的旋转Fourier 互谱和不同桨叶上2 点之间的旋转Fourier 互谱.

已知桨叶以转速n0匀速旋转,半径r i上的一点在t时刻的风速时程幅值为x i,半径r j上的一点在t+τ时刻的风速时程幅值为x j(图2).xi和x j的互相关函数可定义为

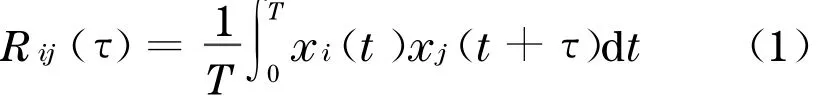
x i和x j的Fourier 互谱可表示为[10]

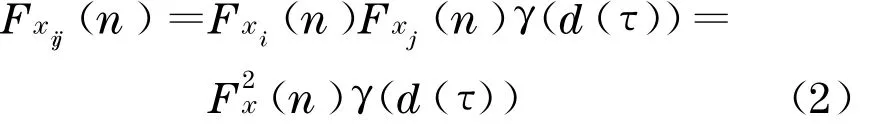
式中,Fxi(n),F xj(n)为随机Fourier 谱,根据随机过程的随机函数描述,可定义为[10]

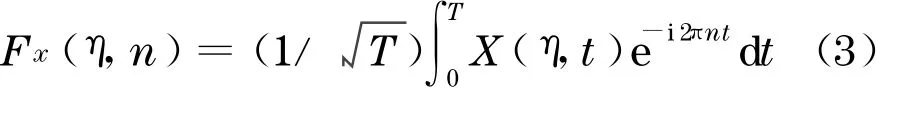
式中:X(η,t)为随机过程样本x(η,t)的集合;η为影响随机激励发展过程且具有物理意义的随机变量或随机向量.文献[11] 由310 组实测风速数据记录识别出随机变量地面粗糙度z0服从对数正态分布,10 m 高平均风速v10服从极值Ⅰ型分布,并最终确定随机Fourier 谱表达式为

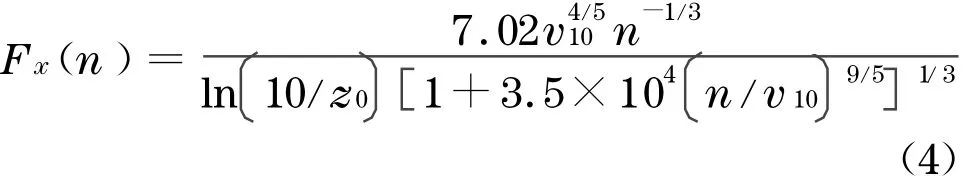
式(2)中,γ(d(τ))为相干函数,其表达式[12]为

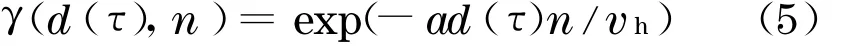
式中:a为衰减常数,一般通过实验获得,文献[13]建议取为10;n为频率;vh为轮毂处平均风速;d(τ)为2 点之间距离(图2).其表达式为

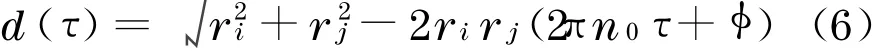
式中,φ为相位因子.当i,j这2 点处于同一片桨叶时,φ=0;处于不同桨叶时,φ则为2π/ Nb(Nb为桨叶数目)的整数倍.对于三桨叶风力发电高塔系统而言,φ始终为2π/3.

Fourier 互谱与互相关函数构成Fourier 变换对.对式(2)逆Fourier 变换,可得两点间的互相关函数为

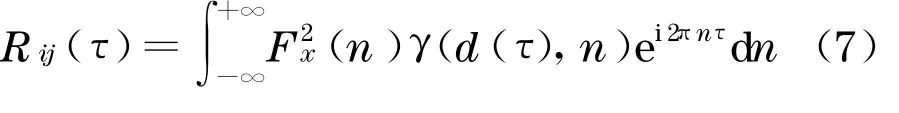
根据旋转Fourier 谱的物理机制,旋转桨叶上任意2 点在不同时刻的旋转互相关函数,可用2 点之间的互相关函数来代替

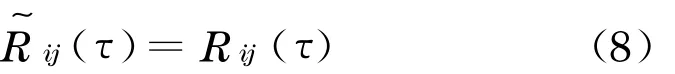
值得注意的是,Rij(τ)为i点与转动时间τ后j点的互相关函数.对旋转互相关函数进行Fourier 变换,可得到旋转Fourier 互谱

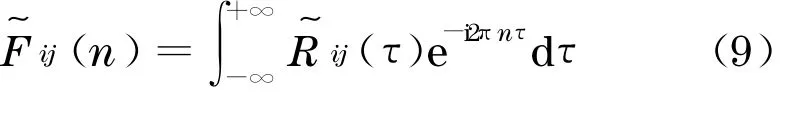
将式(7),(8)代入式(9)中,

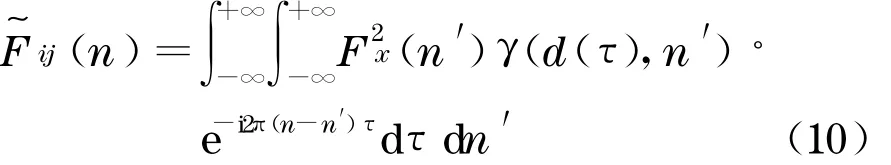
为了分析方便,可将γ(d(τ),n′)进行Fourier 展开

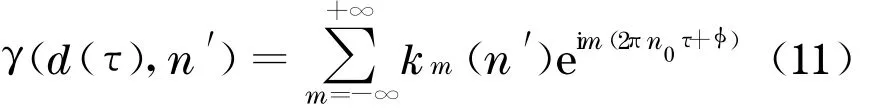
式中:n0为桨叶转动频率;k m(n)为Fourier 展开系数,即

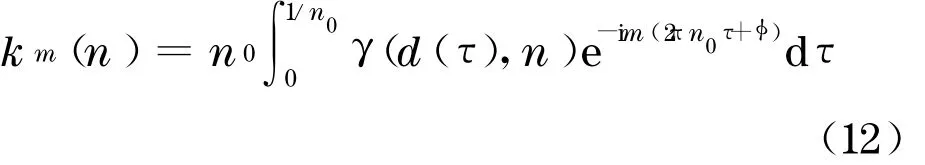
将式(11)代入式(10)中,

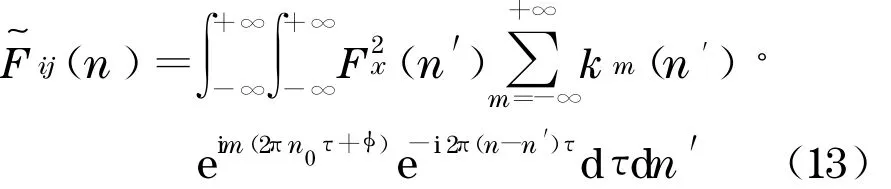
亦即

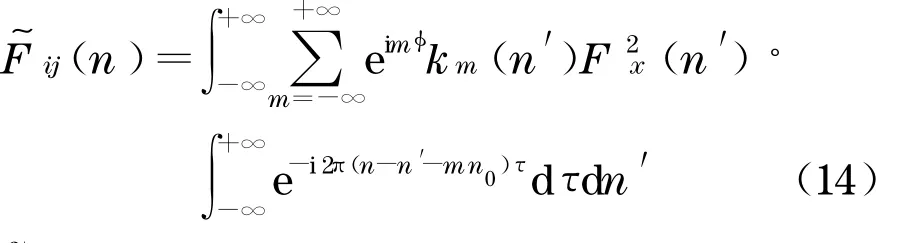
(14)可改写为

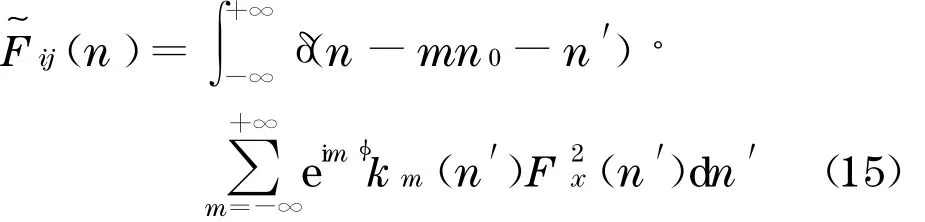
进而可得

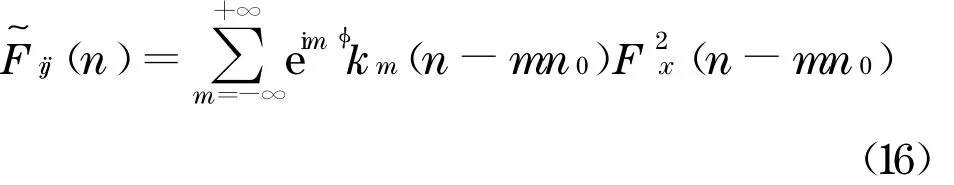
当r i=r j,即相位因子φ=0 时,旋转Fourier互谱退化为旋转Fourier 自谱

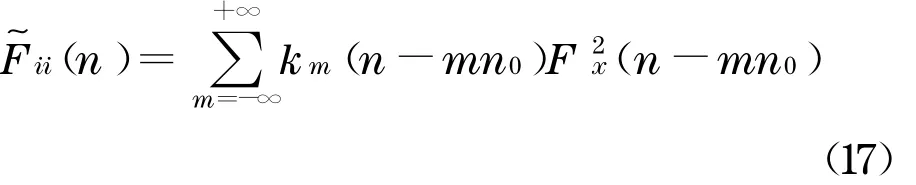
式(17)与文献[9]中的结果是完全一致的.这一结果说明,旋转Fourier 互谱与旋转Fourier 自谱具有统一性.前者具有一般性,而后者是特殊情况下的旋转Fourier 互谱.同时也表明,旋转Fourier 互谱不再是旋转Fourier 自谱与相干函数的乘积.

3 随机风场模拟

3.1 脉动风速

谱和时程这两类描述方法具有等价性,均可以用来描述随机过程.只不过前者是对随机过程的频域描述,后者是对随机过程的时域描述.本质上,样本Fourier 谱和时程共同构成Fourier 变换对.因此,在随机变量给定后,随机函数模型转化为确定性函数,对其逆Fourier 变换即可获得风速时程.基于这一核心思想,以下完成风力发电高塔系统风场仿真.

由旋转Fourier 谱和旋转Fourier 互谱,可共同构造一维多变量零均值随机过程的随机Fourier 谱矩阵如下:

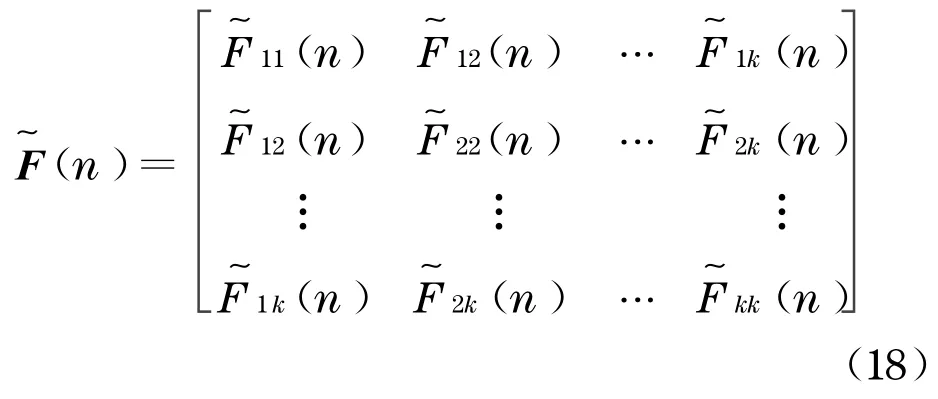
式中,对角线元素由旋转Fourier 幅值谱组成,非对角元素由旋转Fourier 互谱组成.需要说明的是,通常情况下互谱总是复数形式的,但是在风工程中,认为在大气中互谱密度函数的虚部(即正交谱)相比其实部(即互谱)是很小的,工程应用上可以忽略不计[14].从而,这里的旋转Fourier 互谱也就相应地成为了实数的形式,这是在风工程中出现的特例.

为模拟风场, 首先对随机Fourier 谱矩阵进行Cholesky 分解

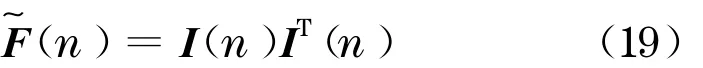
I(n)为下三角矩阵,且有如下形式:

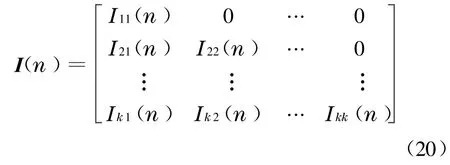
由于随机Fourier 谱矩阵是n的实值偶函数矩阵,所以上式中元素I ij(n)=I ij(-n).根据式(19),将分解后,就可以用下式对目标随机过程v j(t),j=1,2, …,k进行仿真,即

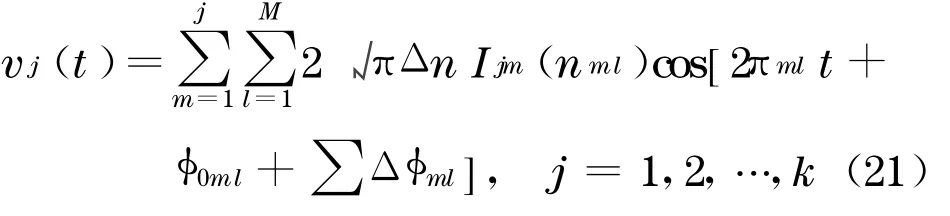
式中:φ0ml为随机初相位角,在[0,2π]区间取值;Δφml为相位差谱[15];n ml为双索引频率,按下式取值:

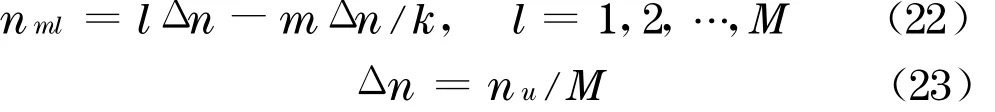
式(23)中,n u为截断频率.由于一般随机Fourier 谱函数的频率分布区间为无穷大,为了数学上处理的方便,有必要设置截断频率n u,认为超过该上限后的随机Fourier 谱函数值为0.由于存在截断频率n u, 可知当M→∞时, Δn→0, 因此, 有n u=MΔn.截断频率的值由在区间[0,n u]和区间[0, ∞]中随机Fourier 幅值谱下包含的面积之比来确定,通常要求该比例接近于1.可按下述公式表示该准则:

同时,为了防止混叠,根据采样定理,在使用式(21)生成时程样本时,时间步长Δt应满足如下条件

塔体脉动风速生成与桨叶相似,只需将旋转Fourier 谱换成随机Fourier 谱即可.限于篇幅,兹不赘述.

3.2 平均风速

对于风力发电高塔系统而言,风剪模型通常采用指数模型

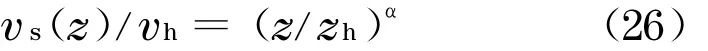
式中:vh为轮毂高度处的平均风速;zh为轮毂高度;α为风速廓线指数.

对于旋转桨叶上的任意一点,其高度z因桨叶旋转而呈现周期性变化

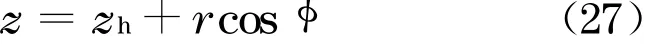
式中:r为计算半径,指风轮旋转平面内任意一点与轮毂中心之间的距离;φ=Ωt,为该点在风轮平面的方位角,正上方时为0°, Ω为桨叶旋转速度.

将式(27)代入式(26)中,可得桨叶上半径r处的平均风速vs(r)为

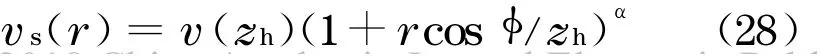
4 数值算例

以典型的1.25 M W 三桨叶变桨距风力发电高塔系统为例,进行风场仿真研究.该风力发电高塔系统轮毂高度为68 m,风轮直径为64 m,桨叶转速为21.1 r ·min-1(0.352 Hz).根据有限元方法,对风力发电机整体结构进行离散,每片桨叶等效为3 个均匀分布的集中质点,三片桨叶一共为9 个集中质点.塔体(机舱)等效为非均匀分布的6 个集中质点,各点的具体位置依据计算方便原则选定,其简化动力计算模型如图3 所示.等效集中质点为动力计算时需要输入风速时程的计算点,这里主要模拟这些点上的风速时程.

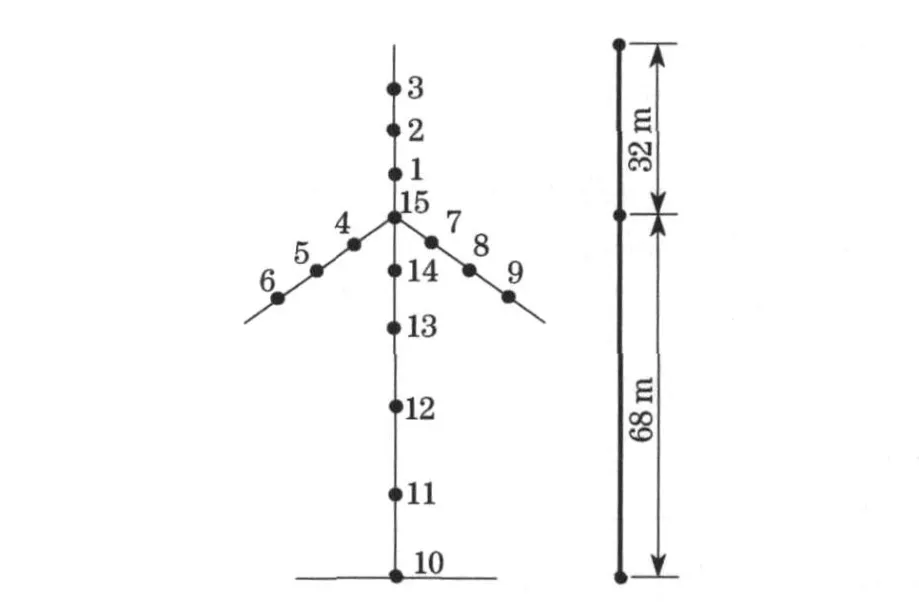
图3 风力发电高塔系统计算点Fig.3 Computing points of the wind turbine system

根据式(24),可确定截断频率nu.结合实际需要,这里取nu=10 Hz.总频点数取为M=2 048.继而由式(23)可得,Δn=0.004 88 Hz.编制Matlab 程序仿真脉动风速时程.表1 给出了塔体第10 ～15 点处的平均风速.图4 给出了塔体第10 ～15 点的仿真脉动风速时程.不难发现,不同点的风速时程之间存在一定的相关性,且相关程度随着2 点距离的增加而减少.例如,相邻点风速时程之间的相似程度要大于非相邻点.

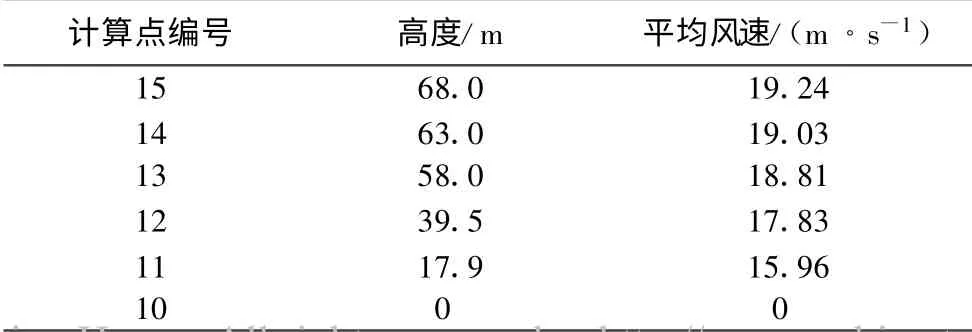
表1 塔体各计算点的平均风速Tab.1 Mean wind velocities at the computing points of the wind turbine tower

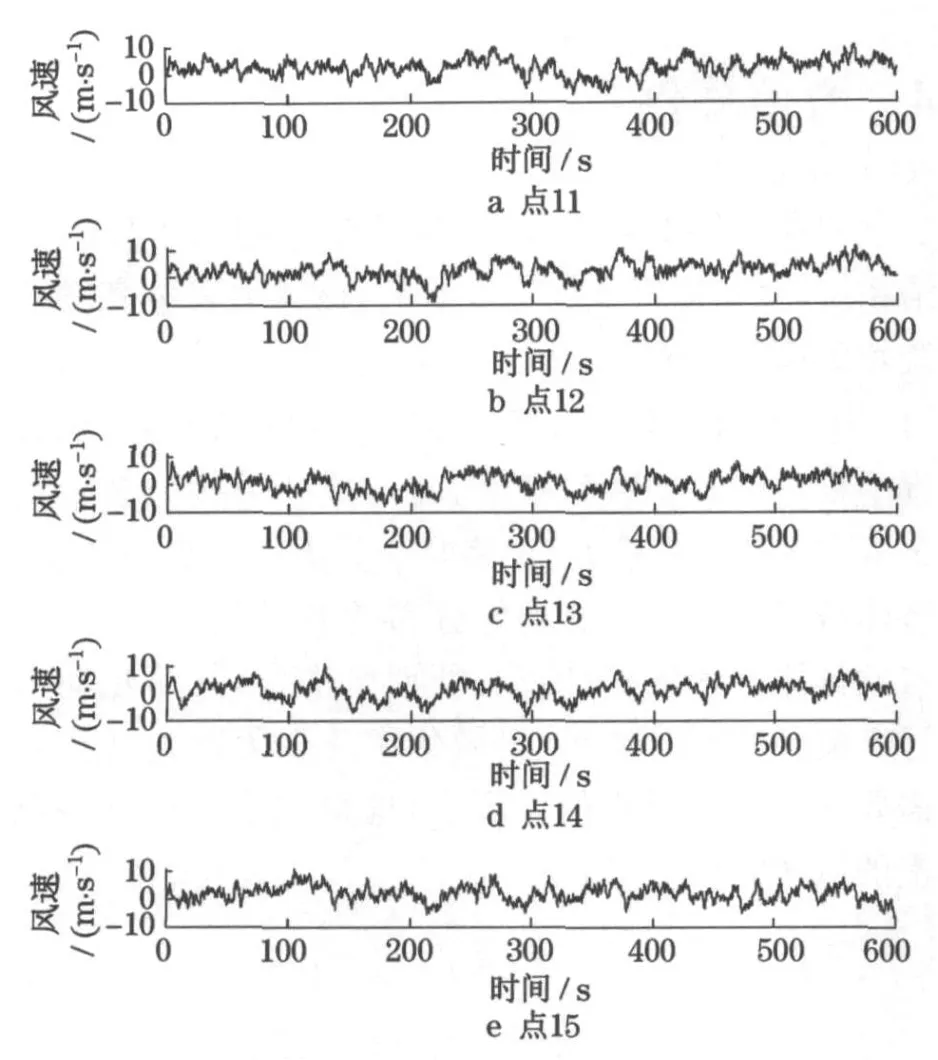
图4 塔体各计算点的仿真脉动风速时程Fig.4 Fluctuating wind velocities at the computing points of the wind turbine tower

图5 给出了桨叶第1 ～3 点处的平均风速时程,图6 给出了3,6,9 点处的平均风速时程.总体上,旋转桨叶上各点的平均风速具有如下特点:①平均风速不再为定值,而呈谐波规律变化;②计算点半径越大,风速波动幅度越大,如点2 的波动幅度大于点1,点3 的波动幅度大于点2;③不同桨叶之间风速不同步,相邻桨叶之间存在2π/nb(nb为桨叶数目)的相位差.桨叶1,2,3 要落后于桨叶4,5,6,而4,5,6落后于7,8,9,它们之间的相位差均为2π/3.

图7 给出了桨叶第1 ～3 点处的脉动风速时程.图8 给出了固定点风速时程(基于随机Fourier 谱的风速时程)与旋转点风速时程(基于旋转Fourier 谱的风速时程)之间的比较.相比较而言, 基于旋转Fourier 谱的风速时程具有两个基本特点:①风速时程幅值有一定增大,但不是特别显著;②风速时程振动频率有大幅度提高.这点极为显著.造成这些差别的主要原因在于旋转点风速时程不仅体现了风速自身的脉动特性,而且还刻画了旋转桨叶高度周期性变化引起的风速波动.总体上,塔体上某点的脉动风速具有时变性,而旋转桨叶上某点的脉动风速时程具有时变、空间变化双重特性.在考虑桨叶旋转效应之后,桨叶脉动风速时程幅值存在一定增长,振动频率会有大幅度提高,从而必然会对风力发电高塔系统极值荷载和疲劳荷载产生重要影响.这正是研究桨叶旋转效应、提出旋转Fourier 谱的根本意义.

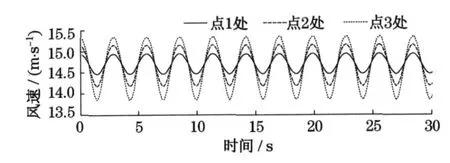
图5 同一桨叶上不同点的平均风速时程比较Fig.5 Mean wind velocities at different computing points of the same blade

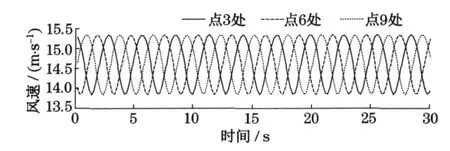
图6 不同桨叶上半径相同点的平均风速时程比较Fig.6 Mean wind velocities at different computing points with the same radius

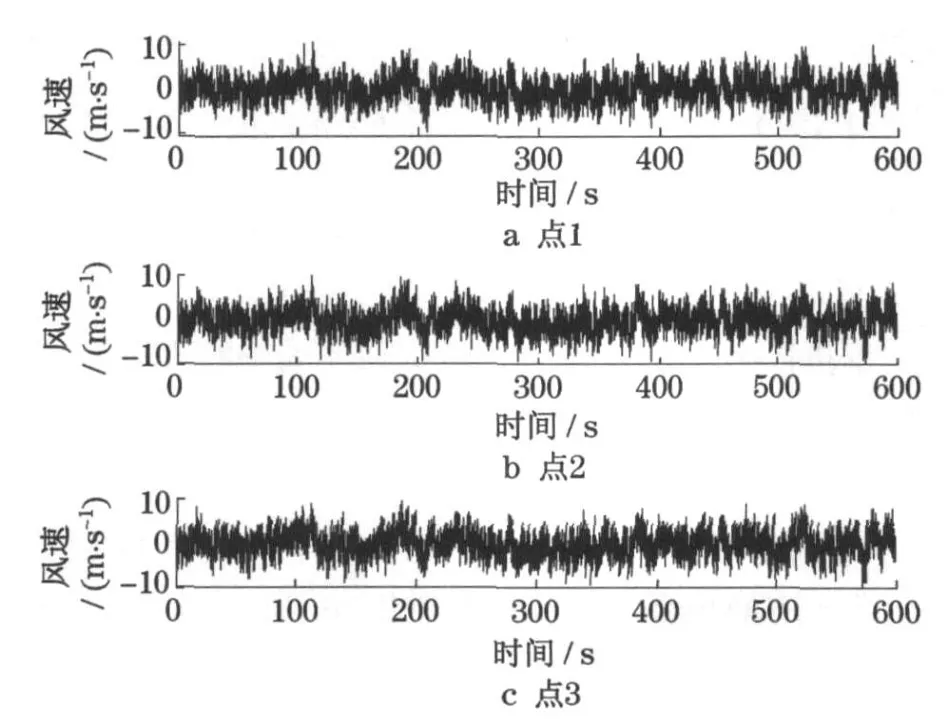
图7 计算点1, 2,3 处的脉动风速时程Fig.7 Fluctuating wind velocities at computing points 1,2 and 3

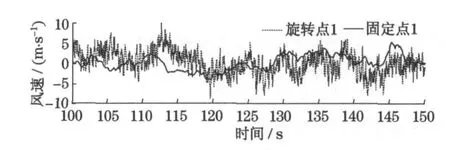
图8 旋转点风速时程与固定点风速时程比较(100～150 s)Fig.8 Comparison between the fluctuating wind velocities of the rotating point and the stationary point(100～150 s)

图9 给出了桨叶第3 点处仿真脉动风速时程的计算旋转Fourier 幅值谱和目标旋转Fourier 幅值谱的比较图,其中,旋转Fourier 幅值谱是由模拟生成的10 000 次、持时为600 s 的风速时程的Fourier 变换幅值经平均计算得到,而目标旋转Fourier 幅值谱是将T=600 s,z0=0.029 m 和v10=14.71 m ·s-1代入表达式(16)得到.其他各点的分析结果与第3点相似,兹不赘述.结果表明,仿真脉动风速时程符合结构所在场地风荷载统计特性,满足了模拟仿真的要求.

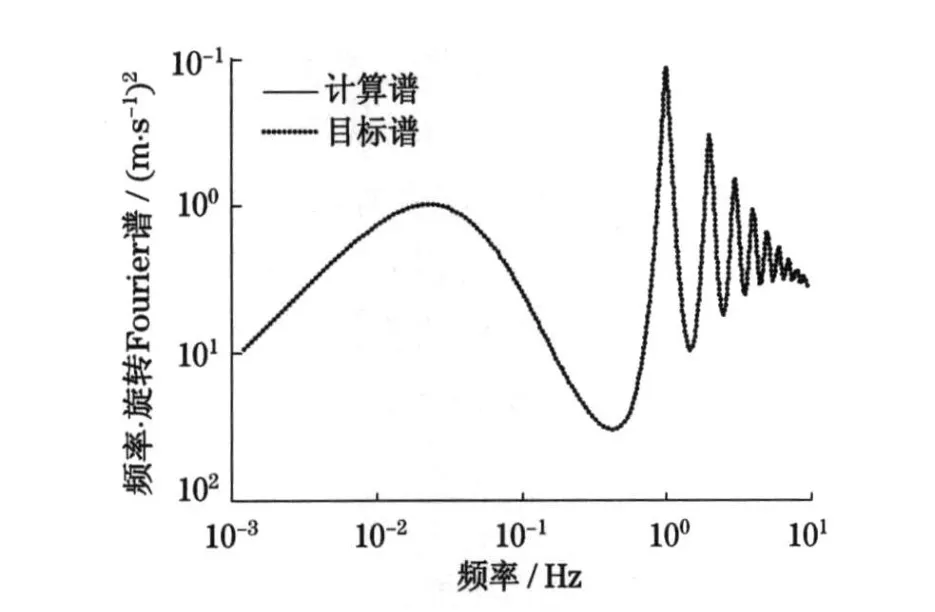
图9 点3的计算旋转Fourier 谱与目标旋转Fourier 谱比较Fig.9 Comparison between the numerical rotational Fourier spectrum and the target rotational Fourier spectrum(point 3)

5 结语

基于物理机制的旋转Fourier 互谱,准确反映了作用在旋转桨叶上风速随机过程的物理本质,有效地考虑了桨叶的旋转效应,并体现了桨叶上不同点风速之间的相关性,为准确确定桨叶风荷载奠定了基础.

实现了风力发电高塔系统的风场模拟.风力发电高塔系统风场模拟可分为桨叶、塔体两部分.其中,桨叶风场模拟需考虑桨叶旋转效应.依据本文风速谱的建模机制,桨叶(塔体)风场模拟本质上为旋转Fourier 谱(随机Fourier 谱)的逆Fourier 变换过程.研究表明,计算旋转Fourier 幅值谱与目标旋转Fourier 幅值谱吻合良好,本仿真算法可以合理地模拟作用于风力发电高塔系统的风速时程.

[ 1] Rice S O.Mathem atical Analysis of Random Noise[ C] ∥Selected Papers on Noise and Stochastic Processes.Dover:[ s.n.] ,1954:133-294.

[ 2] Schueller G I,Shinozuka M.Stochastic methods in structural dynamics[ M] .Dordrecht:Martinus Nijhoff Publishers,1987.

[ 3] Iannuzzi A,Spinelli P.Artificial wind generation and structural response[ J] .Journal of Structural Engineering, ASCE, 1987,113(12):2382.

[ 4] Naganuma T , Deodatis G, Shinozuka M.ARM A m odel for tw o-dim ensional process [ J ] .Journal of Engineering Mechanics,ASME,1987,113(2):234.

[ 5] Yamada M, Ohkitani K.Orthonormal w avelet analysis of turbulence[ J] .Fluid Dy namics Research,1991(8):101.

[ 6] Kitagaw a T,Nomura T .A wavelet-based m ethod to generate artificial w ind fluctuation data[ J] .Journal of w ind engineering and industrial aerodynamics,2002,90:943.

[ 7] 李杰,陈建兵.概率密度演化方程——历史、进展与应用[ R] .上海:同济大学土木工程学院建筑工程系,2009.LI Jie, CH EN Jianbing.Probability density evolution equation—history , development and application [ R ] .Shang hai:Tongji University.Department of Building Engineering,2009.

[ 8] 李杰,张琳琳.脉动风速功率谱与随机Fourier 幅值谱的关系研究[ J] .防灾减灾工程学报,2004,24(4):363.LI Jie,ZHANG Linlin.A study on the relationship between turbulence pow er spectrum and stochastic Fourier amplitude spectrum [ J] .Journal of Disaster Prevention and Mitigation Engineering,2004,24(4):363.

[ 9] 贺广零,李杰.风力发电塔基于物理机制的旋转Fourier 谱[ R] .上海:同济大学土木工程学院建筑工程系,2008.H E Guangling, LI Jie.Rotational Fourier spectrum of wind turbine systemsbased on phy sical mechanism [ R] .Shanghai:Tongji University.Department of Building Engineering,2008.

[ 10] 李杰.工程结构随机动力激励的物理模型[ R] .上海:同济大学土木工程学院建筑工程系,2008.

LI Jie.Physical stochastic models for the dy namic excitations of engineering structures [ R] .Shanghai:Tong ji University.Department of Building Engineering,2008.

[ 11] 李杰,张琳琳.实测风场的随机Fourier 谱研究[ J] .振动工程学报,2007,20(1):66.LI Jie, ZHANG Linlin.Research on the random Fourier spectrum of observational wind [ J] .Journal of Vibration Engineering,2007,20(1):66.

[ 12] World Meteorological Organization.M eteorological aspects of the utilizationof wind as an energy source [ R] .WMO Technical Note No.175 World M eteo rological Organization,Geneva 1981.

[ 13] Drag t J B.T he spectra of w ind speed fluctuations m et by a rotating bladeand resulting load fluctuations[ C] ∥Proceedings of European Wind Energy Conf 1984.H am burg:[ s.n] , 1984:453-459.

[ 14] Simiu E, Scanlan R H .Wind effects on structures:an introduction to w ind engineering [ M ] .New York:John Wiley,1978

[ 15] 艾晓秋.基于随机地震动模型的地下管线地震反应及抗震可靠度研究[ D] .上海:同济大学建筑工程系,2005.AI Xiaoqiu.Stochastic earthquake model-based research on seismic responseand reliability of underground pipelines [ D] .Shang hai:Tongji University.Department of Building Engineering,2005.