吲哚咔唑异构体的电子结构和光学性质
王会萍 白福全 郑清川 赵增霞 赵晓杰 张红星
(吉林大学理论化学研究所,理论化学计算国家重点实验室,长春 130023)
吲哚咔唑异构体的电子结构和光学性质
王会萍 白福全 郑清川 赵增霞 赵晓杰 张红星*
(吉林大学理论化学研究所,理论化学计算国家重点实验室,长春 130023)
分别采用密度泛函理论(DFT)和单激发组态相互作用(CIS),在6-31G(d,p)基组水平上优化了5个吲哚咔唑分子的基态和激发态结构.在此结构的基础上,用含时密度泛函理论(TD-DFT)在相同基组水平和极化连续介质模型(PCM)下计算了模型分子的吸收和发射光谱.这几个吲哚咔唑异构体的发射光谱有明显的差别,如异构体5 ([3,2-b]型)有较大的振子强度,但是相对于其他异构体,其发射能量最小;异构体4([3,2-a]型)的发射能量最大;异构体2([2,3-b]型)的最大振子强度在250-450 nm范围内,与其他几个分子相比为最小.这主要是由分子的激发态几何变化和轨道能级的不同导致的.本文还考察了这类分子的一阶超极化率,结果显示5个分子极化率在同一水平,但静态第一超极化率(β0)有明显差别,异构体2的β0值最大.
密度泛函理论;含时密度泛函理论;吲哚咔唑;单激发组态相互作用方法;吸收和发射光谱;非线性响应
吲哚咔唑在浩瀚的杂环化合物中组成一类重要的家族[1].吲哚部分通过一个共用的C—C键(指苯环中的碳碳键,下同)缚在咔唑的苯环部分构成吲哚咔唑分子,具有类似并五苯的稠环结构.5个经过实验检验的异构体被命名为:[2,3-a]吲哚咔唑(1),[2,3-b]吲哚咔唑(2),[2,3-c]吲哚咔唑(3),[3,2-a]吲哚咔唑
(4),[3,2-b]吲哚咔唑(5).这5个分子以不同的共用C—C键位置和不同的N原子端的方位来区别.
众多的自然界天然产物中镶嵌有吲哚咔唑骨架,这些化合物展示了有趣的生物学性质,同时推动了本领域的发展[2-4].作为蛋白酶抑制剂被研究较多的是吲哚咔唑衍生物——生物碱k-252a,还有分子3显示了良好的生物活性,由其派生出的大配体可作为芳烃接受体[5-7].5个异构体分子有些虽然在自然界中产量不高,但是这类化合物一般都具有较大的带隙和较低的最高占据分子轨道(HOMO)能级,这类分子的大共轭平面结构有助于载流子的传输,而且其大平面刚性结构使得这类化合物具有良好的热稳定性.所以基于其具有良好的发光性能和潜在应用前景已被视为热门研究对象,因此在其生物活性被关注的同时,作为分子材料在材料应用研究等方面也逐渐变得热门,并显示出较大的应用潜力[8-10],当然其衍生物的应用与非线性光学材料的研究也伴随着开展起来[9,11].基于这类分子骨架的重要性,我们应用理论计算方法研究了这5个异构体分子的电子结构和光谱性质,以期对实验研究提供有力的理论支持.
1 理论方法
模型分子1-5的优化结构如图1所示.它们的对称性分别为:1-3,C2v;4,Cs;5,C2h.本文采用密度泛函理论(DFT)[12,13]中的B3LYP[14,15]方法和单激发组态相互作用(CIS)方法[16]分别优化了分子的基态和激发态构型.对所有原子应用6-31G(d,p)基组进行计算.基于实验光谱数据是在二氯甲烷溶液中测得,我们应用极化连续介质模型(PCM)[17]来模拟溶剂环境,采用含时密度泛函(TD-DFT)方法[18,19]进行激发能的计算,并将计算结果拟合成光谱曲线.
当分子处于一个微弱并均匀恒稳的外加电场中,能量表示为[20]

式中E0是没有外加电场时的分子总能量,F为外加电场,μ、α、β、γ依次分别表示偶极距、极化率、第一超极化率和第二超极化率.脚标i、j、k、l表示相应张量的分量.
静态第一超极化率公式为

其中,βi=3(βiii+βijj+βikk)/5,i,j,k=x,y,z.
极化率和超极化率通过有限场(FF)方法计算得到[21-23].外加电场从0.0005-0.0015 a.u.变化时,计算得到的数值变化不大,因此本文列出数据是在0.0010 a.u.电场情况下得到的.
本文的所有计算工作是采用Gaussian 03程序[24]完成的.
2 结果与讨论
2.1 吲哚咔唑分子几何构型
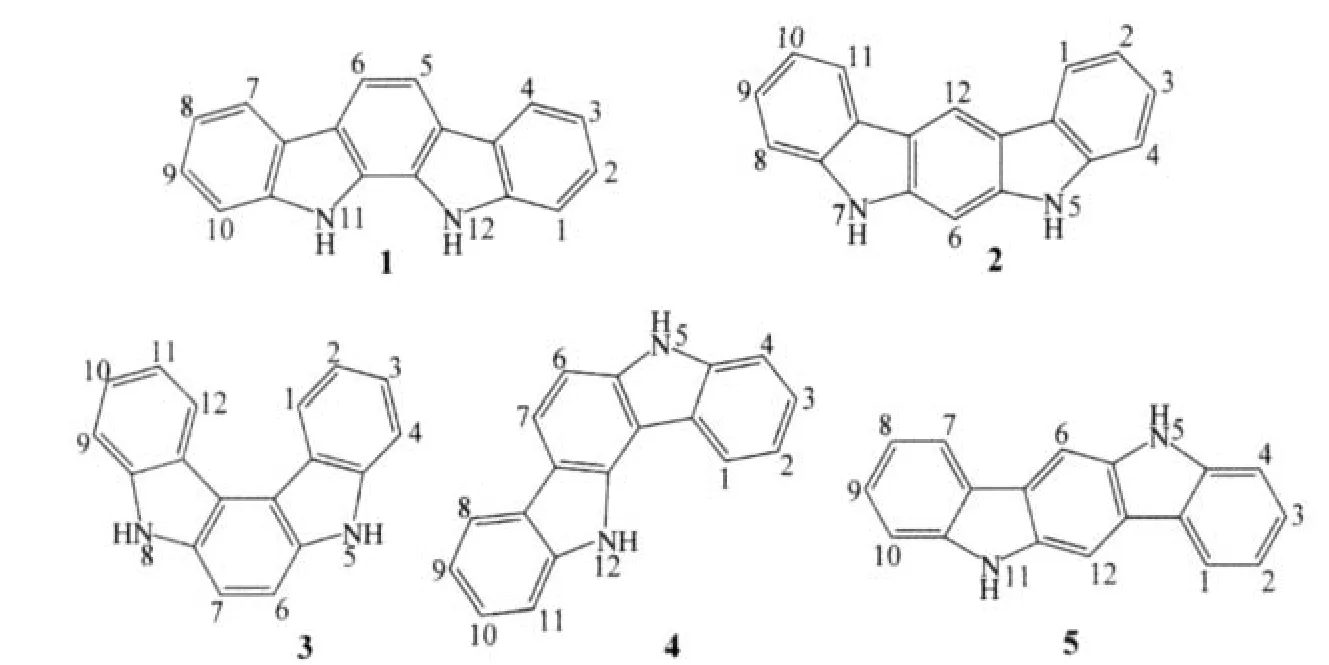
图1 模型分子1-5的结构图Fig.1 Sketches of the model molecules 1-5
基于单分子模型优化分子几何结构.激发态构型优化时采用对称性保持和对称性放松两种条件,比较计算结果发现,对称性保持条件下分子整体具有更低的激发态能量,光谱结果也与实验[22,23]符合得较好.5个分子基态和激发态结构变化的共同点是位于两端的苯环键长在激发态时收缩;中间苯环的6个C—C键长变得不均匀;与中间苯环相连的一侧的N—C键长变化比另一侧的N—C键明显.以异构体1和4为例,将基态和激发态键长变化绘于图2中.结构变化不同点是变化程度不同,[2,3]向异构体1-3的两侧苯环收缩程度小于[3,2]向异构体4和5;异构体2的中间苯环变化程度较小;整体来看5个分子中1和5的变化程度最大.
2.2 模拟吸收和发射光谱结果
图3是在B3LYP/6-31G(d,p)水平下计算得到的异构体1-5基态的HOMO和最低空轨道(LUMO)图.HOMO轨道主要是π成键轨道,而LUMO轨道主要表现为π*反键轨道.除了异构体4,其他分子中N原子上的p轨道没有与苯环平面形成有效的p-π共轭,而LUMO轨道中几乎没有N原子的p轨道贡献.这与咔唑分子情形较为相似[25].4中的一个N原子在HOMO轨道中形成一个有效的p-π共轭形式,虽然N原子上p轨道在LUMO轨道中的成分比例减小了,但是仍高于其他4个分子.从分子轨道出发可以得出,通过修饰4的N原子一侧则可有效影响[3,2-a]型衍生物分子的轨道性质.
经高斯曲线拟合的吸收和发射光谱见图4.吸收曲线[图4(A)]特点为两个明显的吸收峰,最低能吸收(>280 nm)主要是从HOMO到LUMO轨道的跃迁,亦即分子内五个圆环中的固定在每个圆环内的π-π*跃迁;而高能吸收峰(200-280 nm)为N原子杂环与苯环间的π-π*跃迁.异构体4在高能区吸收峰较为宽阔,这主要是由于跃迁中有更多比例的N原子成分参与的结果.表1中列出了异构体1和4的垂直激发能大小和实验测得的吸收峰值,结果显示1和4的激发能与实验吸收波长符合较好.细微差别被认为来自实验分子的中间苯环上甲基取代基的影响[26].这个结果证实了针对于这类分子的模拟方法能够提供较好的计算结果.

图2 异构体1和4基态和激发态的优化结构和键长(单位:nm)Fig.2 Optimized structures and bond lengths(unit in nm)in ground and excited states for isomers 1 and 4

图3 异构体1-5基态的HOMO和LUMO轨道示意图Fig.3 The highest occupied molecular orbital(HOMO)and the lowest unoccupied molecular orbital(LUMO) plots of isomers 1-5 in ground states

图4 CH2Cl2溶液中经高斯曲线拟合的异构体1-5的吸收(A)与发射(B)光谱Fig.4 Simulated absorption(A)and emission(B)spectra of isomers 1-5 in CH2Cl2solution
虽然异构体的吸收光谱差别较小,但1-5的发射光谱[图4(B)]结果表现出明显差别.首先,1和5的发射峰相对于最低能吸收位移较大,这主要是因为激发态几何变化中1和5也是最明显的,较大的键长变化使得1和5的HOMO-LUMO能隙变小.表2列出了1和4的发射跃迁特征及相关实验值.从表2看出,1的最低能发射主要来自于LUMO→HOMO-1而不是LUMO→HOMO,但通过对称性可知,LUMO→HOMO-1(7b1→6b1)和其最低能吸收HOMO→LUMO(6b1→7b1)是对应的,其余几个分子的最低能发射亦是同样来自于最低能吸收.比较振子强度(f)发现,1的以LUMO→HOMO为主的跃迁具有大的振子强度,是1发射光谱的主要特征.其次,2-4具有两个发射峰,这主要是由于2-4基态和激发态分子构型变化较小,环内π-π*跃迁和环间的π-π*跃迁都在发射光谱中得到体现.可以总结出来1和5两种直线型分子激发态构型变化大,但是电荷转移跃迁的振子强度也大;而2-4基于构型特点易于保持高能发射,但振子强度较小.比较结
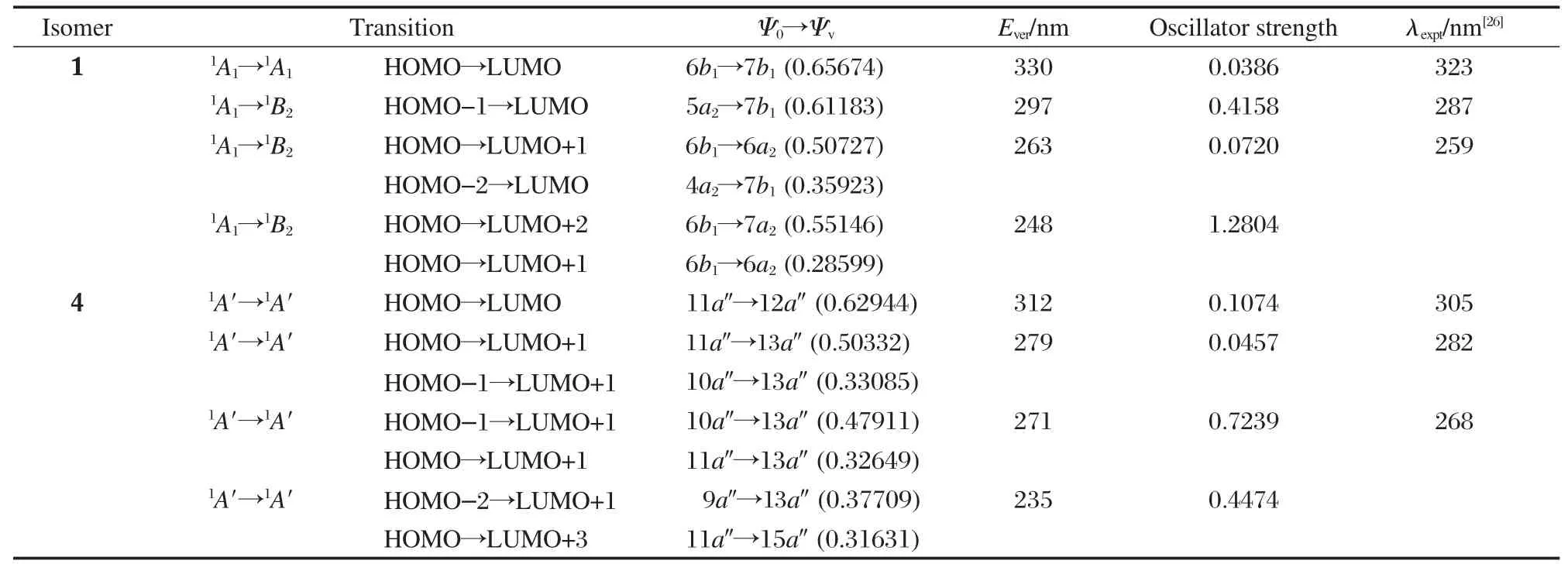
表1 TD-DFT方法计算得到的CH2Cl2溶液中异构体1和4的吸收性质Table 1 Absorption properties of isomers 1 and 4 in CH2Cl2solution obtained with the TD-DFT calculations
Ψ0:occupied orbital,Ψv:unoccupied orbital,Ever:vertical excitation energy;The data in the parentheses according to the column“Ψ0→Ψv”are configuration interaction coefficients.果,这几个分子中2的振子强度最小.

表2 TD-DFT方法计算得到的CH2Cl2溶液中1和4的发射性质Table 2 Emission properties of isomers1 and 4 in CH2Cl2solution according to the TD-DFT calculations

表3 异构体1-5的偶极矩(μ)、极化率(α)和静态第一超极化率(β0)计算结果Table 3 Calculated dipole moments(μ), polarizabilities(α),and the static first hyperpolarizabilities(β0)of isomers 1-5
2.3 吲哚咔唑异构体的第一超极化率
本文还考察了几个分子的极化率与第一超极化率结果.表3列出了计算得到的几类参数,虽然几个分子的极化率非常接近(210-225 a.u.),但它们的静态第一超极化率(β0)值有显著的不同.从“态求和”公式得出,β0∝fΔμge(Ege)-3[27],其中Δμge为基态和激发态偶极矩差,Ege为跃迁能.2的β0值较大是三种因素的乘积较大的缘故.虽然这个量级(102)的β0值不足以直接应用于非线性光学材料,但本文计算得到的这种差别为在此基础上的材料设计提供了思路,如延展2两侧共轭环,那么β0值将会进一步增加.
3 结 论
通过和实验结果比较,我们得到了和实验结果符合较好的较为精确的理论计算结果.5个吲哚咔唑异构体分子因几何结构的不同带来性质上的明显差异.首先,呈线型的分子构型如1([2,3-a]型)和5([3,2-b]型)导致基态到激发态间结构变化显著,而且线型分子有助于提高环间电荷转移跃迁的振子强度.其他非直线型分子中,4([3,2-a]型)的N原子相反取向导致分子轨道能级易受修饰N原子影响.5个分子的非线性响应特征差别明显,2([2,3-b]型)因较大的激发态偶极矩变化和较大的跃迁能使得其非线性响应在这5个异构体中最为显著.本文的计算结果为以吲哚咔唑作为应用单元的光学材料设计提供了理论基础.
1 Janosik,T.;Wahlström,N.;Bergman,J.Tetrahedron,2008,64: 9159
2 Prudhomme,M.Curr.Pharm.Des.,1997,3:265
3 Prudhomme,M.Curr.Med.Chem.-Anti-Cancer Agent,2004,4: 509
4 Bergman,J.;Janosik,T.;Wahlström,N.Adv.Heterocycl.Chem., 2001,80:1
5 Sezaki,M.;Sasaki,T.;Nakazawa,T.;Takeda,U.;Iwata,M.; Watanabe,T.;Koyama,M.;Kai,F.;Shomura,T.;Kojima,M. J.Antibiot.,1985,38:1437
6 Yasuzawa,T.;Iida,T.;Yoshida,M.;Hirayama,O.;Takahashi,M.; Shirahata,K.;Sano,H.J.Antibiot.,1986,39:1072
7 Rannug,U.;Rannug,A.;Sjöberg,U.;Li,H.;Westerholm,R.; Bergman,J.Chem.Biol.,1995,2:841
8 Zhao,H.P.;Tao,X.T.;Wang,P.;Yan,R.;Yang,J.X.;Yan,Y.X.; Yuan,C.X.;Liu,H.J,;Zou,D.C.;Jiang,M.H.Org.Electron., 2007,8:673
9 Ooyama,Y.;Kagawa,Y.;Harima,Y.Eur.J.Org.Chem.,2007, 22:3613
10 Lai,W.Y.;Chen,Q.Q.;He,Q.Y.;Fan,Q.L.;Huang,W.Chem. Commun.,2006:1959
11 Ooyama,Y.;Shimada,Y.;Kagawa,Y.;Imae,I.;Harima,Y.Org. Biomol.Chem.,2007,5:2046
12 Hohenberg,P.;Kohn,W.Phys.Rev.B,1964,136:864
13 Kohn,W.;Sham,L.J.Phys.Rev.A,1965,140:1133
14 Becke,A.D.J.Chem.Phys.,1993,98:5648
15 Lee,C.;Yang,W.;Parr,R.G.Phys.Rev.B,1988,37:785
16 Foresman,J.B.;Head-Gordon,M.;Pople,J.A.;Frisch,M.J. J.Phys.Chem.,1992,96:135
17 Cossi,M.;Scalmani,G.;Rega,N.;Barone,V.J.Phys.Chem., 2002,117:43
18 Casida,M.E.;Jamorski,C.;Casida,K.C.;Salahub,D.R.J.Phys. Chem.,1998,108:4439
19 Zhang,J.P.;Zhou,X.;Bai,F.Q.;Zhang,H.X.Acta Phys.-Chim. Sin.,2008,24:2243 [张建坡,周 欣,白福全,张红星.物理化学学报,2008,24:2243]
20 Long,M.J.;Williams,C.K.Angew.Chem.Int.Edit.,2003,42: 2586
21 Cohen,H.D.;Roothaan,C.C.J.J.Chem.Phys.,1965,43:S34
22 Kurtz,H.A.;Stewart,J.J.P.;Dieter,K.M.J.Comput.Chem., 1990,11:82
23 Maroulis,G.J.Chem.Phys.,1991,94:1182
24 Frish,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03. Revision C.02.Pittsburgh,PA:Gaussian Inc.,2003
25 Bo,D.S.;Ren,A.M.;Feng,J.K.;Yang,L.Chem.J.Chin.Univ., 2007,28:955 [薄冬生,任爱民,封继康,杨 丽.高等学校化学学报,2007,28:955]
26 Tsuchimoto,T.;Matsubayashi,H.;Kaneko,M.;Nagase,Y.; Miyamura,T.;Shirakawa,E.J.Am.Chem.Soc.,2008,130:15823
27 Tretiak,S.;Chernyak,V.;Mukamel,S.Chem.Phys.Lett.,1998, 287:75
August 31,2009;Revised:November 16,2009;Published on Web:December 1,2009.
Electronic Structures and Optical Properties of Indolocarbazole Isomers
WANG Hui-Ping BAI Fu-Quan ZHENG Qing-Chuan ZHAO Zeng-Xia ZHAO Xiao-Jie ZHANG Hong-Xing*
(State Key Laboratory of Theoretical and Computational Chemistry,Institute of Theoretical Chemistry,Jilin University, Changchun 130023,P.R.China)
Density functional theory(DFT)and the configuration interaction with single excitations(CIS)method were used to optimize the ground state and excited state structures of five indolocarbazole molecules using the 6-31G (d,p)basis set.Based on their geometric structures,the absorption and emission spectra were calculated using timedependent DFT(TD-DFT)with the same basis set and employing the polarizable continuum medium model(PCM). There are obvious differences in the emission spectra of these isomers as isomer 5 has larger oscillator strength in its emission spectrum,but its transition energies are the lowest among the isomers.The emission peak value of isomer 4 is the highest and the oscillator strengths of isomer 2 are the weakest from 250 to 450 nm.This is because the structures change from ground state to the excited state and the molecular orbital(MO)energy levels of these molecules are different.We also evaluated the nonlinear optical response(first hyperpolarizability)of this series of molecules.The calculated polarizabilities are similar but the static first hyperpolarizabilities(β0)are different.The β0of isomer 2 is the largest among the compounds investigated.
Density functional theory; Time-dependent density functional theory; Indolocarbazole; Configuration interaction with single excitation method; Absorption and emission spectra; Nonlinear optical response
O641
*Corresponding author.Email:zhanghx@jlu.edu.cn;Tel:+86-431-88498966.
The project was supported by the National Natural Science Foundation of China(20573042,20333050).
国家自然科学基金(20573042,20333050)资助项目

