结合神经网络方法和扩大训练基组构建新B3LYP泛函

张家虎 王秀军

(华南理工大学化学与化工学院应用化学系,广州 510640)

结合神经网络方法和扩大训练基组构建新B3LYP泛函

张家虎 王秀军*

(华南理工大学化学与化工学院应用化学系,广州 510640)

神经网络方法成功地应用于修正密度泛函理论B3LYP方法中的三个参数(a0、ax和ac)以构建新B3LYP交换相关泛函.本文采用包含输入层、隐藏层和输出层的三层式神经网络结构.总电子数、多重度、偶极矩、动能、四极矩和零点能被选为物理描述符.296个能量数据被随机地分成两组,246个能量数据作为训练集以确定神经网络的最优结构和最优突触权重,50个能量数据作为测试集以测试神经网络的预测能力.修正后的三个参数ã0、ãx、ãc从输出层处得到,并用于计算体系的热化学性质如原子化能(AE)、电离势(IP)、质子亲合能(PA)、总原子能(TAE)和标准生成热(ΔfH⊖).修正后的计算结果优于传统B3LYP/6-311+G(3df,2p)方法的计算结果.经过神经网络修正后,296个物种的总体均方根偏差从41.0 kJ·mol-1减少到14.2 kJ·mol-1.

B3LYP泛函;神经网络;描述符;训练基组

密度泛函理论(DFT)以其良好的计算性能和较低的计算成本,成为化学家和物理学家理解原子、分子、固体及其相关电子结构的一个非常宝贵的工具[1],并且成为化学、凝聚态物理、材料科学和分子生物学中重要的研究工具[2,3].尽管DFT在实际应用中取得了很大的成功,但是它通常并不能足够准确地预测分子的实验值,尤其是对于大分子体系,偏差产生的原因就在于DFT中的固有近似[4].DFT计算结果的准确度是由其精确交换相关泛函XC泛函决定的[2],而精确交换相关泛函是不知道的.所有的DFT计算均使用近似交换相关泛函,这就进一步扩大了计算结果的偏差.所以寻找更加精确的交换相关泛函对提高DFT计算精度有着重要的意义.

最初的近似交换相关泛函是基于局域梯度近似(LDA)[5],后来广义梯度近似(GGA)[6-9]和杂化泛函[10]的发展对交换相关泛函的发展起了很大的促进作用.交换相关泛函包括局域和非局域贡献,除此之外,高阶项相关能对交换相关泛函的贡献也不可忽视.Chen等[11]讨论了高阶项相关能对B3LYP泛函的贡献.近年来交换相关泛函的一个研究趋势就是利用准确的实验数据确定交换相关泛函表达式中的参数值.例如:Becke使用最小二乘法拟合G2[12,13]基组中原子和分子能量数据,确定了B3LYP泛函表达式中的三参数值[10].

B3LYP泛函在过去的十几年中得到了重大的发展,尤其是在使用B3LYP预测小型和中型分子体系的热化学性质方面[14-16].但是B3LYP计算结果与实验结果之间也存在着较大的偏差.因此,许多学者提出了一些修正模型,如线性回归模型[17,18]、支持向量机模型[19]和神经网络模型[20-25],对B3LYP方法进行修正,极大地改进了计算结果的偏差.这些模型只是对DFT计算结果进行修正,而文献[11]提出了用神经网络来构建B3LYP泛函.本文在此基础上将数据库从116个数据扩展到了296个(116个来自文献[10],180个来自文献[20],文献[10,20]已经考证这些数据的实验值是可靠的),大大地提高了此方法的适用性.

1 计算方法

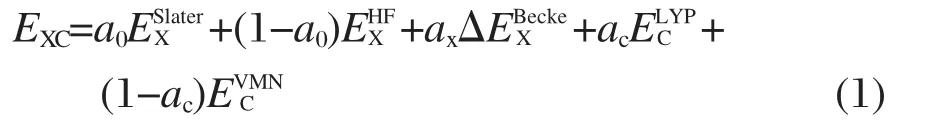
杂化B3LYP泛函可以表示为:高阶项相关能是系统相关的,并且高阶项相关能在式(1)中各项均有体现,因此,式(1)中的三参数也应该是系统相关的.三个参数可以通过神经网络得到.

采用神经网络进行计算时,首先要构建有效的神经网络结构,而构建有效的神经网络结构就要选择能充分反映体系特征性质的物理描述符.由于密度泛函理论是基于体系电子密度的理论,而交换相关泛函也只是电子密度的泛函,因此选择的物理描述符要能反映体系的电子特性.同时,选择的物理描述符要能够反映体系电子的分布,因为电子的分布和电子密度紧密相关.在选取了物理描述符之后,我们就随机选用246个能量数据作为训练集,50个能量数据作为测试集,用训练集确定神经网络的结构,并用此神经网络确定三参数值的校正值.同时,得到新的基于神经网络的B3LYP交换相关泛函.

Perdew等[28,29]在GGA基础上提出了meta-GGA,在meta-GGA中,交换相关泛函不仅是电子密度和密度梯度的泛函,同时也是动能密度的泛函,因此动能Ek被选取为关键物理描述符.电子密度分布ρ(r)唯一地决定着交换相关泛函并且可以从多极矩的角度被扩展,作为零阶项的扩展,总电子个数Ne也被选作是物理描述符.体系的偶极矩和四极矩也是如此,我们选择作为偶极描述符,Q≡作为四极描述符,其中di(i=x,y,z)是偶极矩向量的分量,Qii(i=x,y,z)是四极矩张量的对角分量.因为交换泛函同自旋电子之间的交换作用相关,所以多重度gs也被选作是物理描述符.零点能(ZPE)对能量的校正起着重要的作用,因此了也被选作关键物理描述符.

我们采用三层式的神经网络结构:包括输入层、隐藏层和输出层(见图1).相邻层之间通过突触权重(Wij或)连接.物理描述符gs、Ne、D、Ek、Q和 ZPE的值从输入层输入神经网络.对于每一个原子或分子而言,三参数a0、ax和ac修正后(修正后的三参数表示为ã0,ãx和ãc)的值可以从输出层获得.我们使用246个能量实验值作为训练集,并用它来确定神经网络的结构和突触权重值.我们采用B3LYP/6-311+G(3df,2p)进行计算,每个分子的几何构型直接用B3LYP/6-311+G(d,p)方法优化得到.D、Ek、Q和ZPE的值也由B3LYP/6-311+G(3df,2p)方法计算得出.除了物理描述符gs、Ne、D、Ek、Q和ZPE的值输入输入层之外,偏置量也被引入了输入层和隐藏层,并且偏置量在整个训练过程中保持不变.同时,采用误差反向传播学习方法优化突触权重.对于每一个分子或原子而言,系统相关的三参数ã0、ãx和ãc被用来修正相应的B3LYP泛函,修正后的B3LYP泛函依次用来计算相应的原子化能(AE)、电离势(IP)、质子亲合能(PA)、总原子能(TAE)和标准生成热(ΔfH⊖)的值.修正后的能量值同相应的实验值比较,误差反馈给神经网络,同时,所有的突触权重值获得相应地调整.这个步骤重复进行直到整个训练集能量的计算值和实验值足够的接近.然后,整个神经网络就可被认为是收敛的,突触权重也相应最终确定.

我们将296个能量数据(56个用于计算AE、42个用于计算IP、8个用于计算PA、10个用于计算TAE以及180个用于计算ΔfH⊖)随机地分成大小相近的六组.其中五个用于训练神经网络的权重,称之为训练组.第六组用于检验神经网络的预测效果,称之为验证组.如此重复六次以优化神经网络的结构.我们从1到10改变隐藏神经元的数目,结果表明,8个隐藏神经元效果最好.即:总体均方根偏差以及训练组与验证组的均方根偏差最小.预测组预测结果确保了神经网络的预测效果.因此,我们采用了7-9-3结构(见图1).为了使输出数据同目标数据易于比较,需对输入层描述符(xi)数值进行预处理.除了偏置量之外,每一个xi的值都被换算到区间(0.1, 0.9)内.经神经网络修正的ã0、ãx和ãc值在输出层处获得,并且它们同{xi}之间的关系如下:

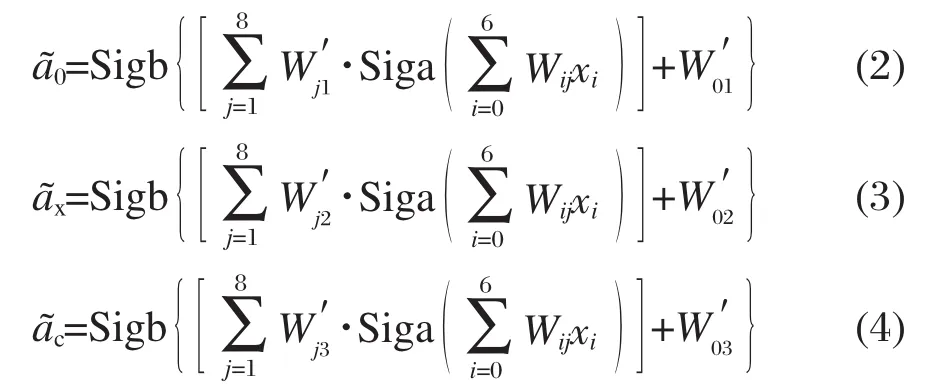
其中,

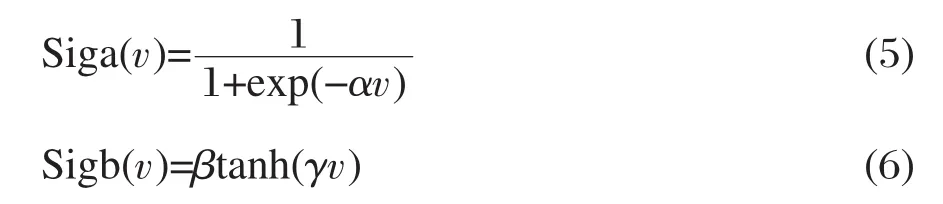
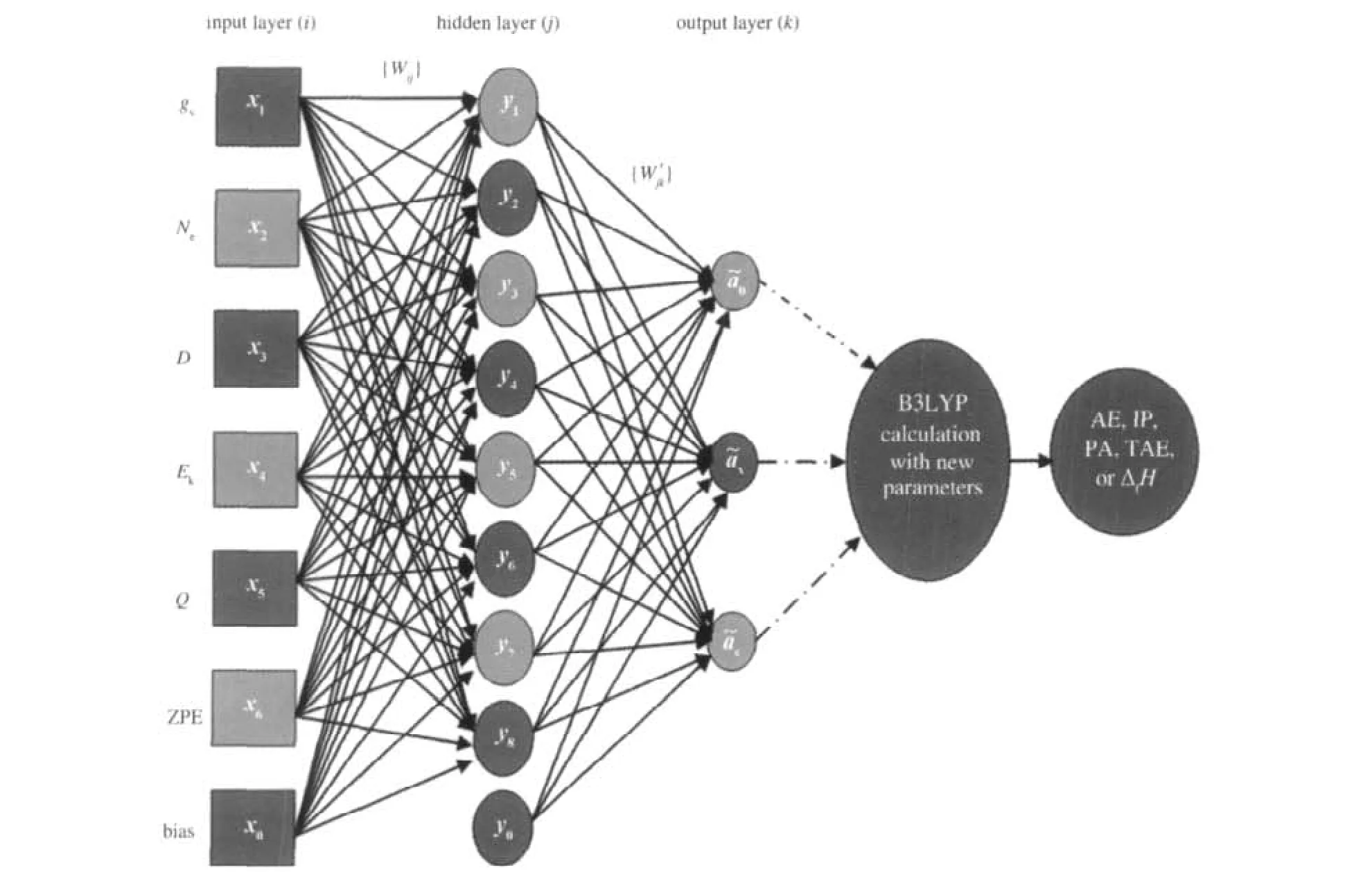
图1 神经网络结构图Fig.1 Architectural graph of the neural networkxi(i=1-6)are spin multiplicity(gs),the total number of electrons(Ne),dipole moment(D),kinetic energy(Ek),quadrupole moment(Q),and zero point energy(ZPE),respectively.yj(j=1-8)are the number of hidden neuron.x0and y0are bias in input layer and in hidden layer,respectively.{Wij}are the synaptic weights connecting the input layer(xi)and the hidden neurons(yj),and{Wj′k}connect the hidden neurons and the output.ã0,ãxand ãcare the modified three parameters in B3LYP method.AE,IP,PA,TAE,and ΔfH⊖are atomic energy,ionization potential,proton affinity,total atomic energy, and standard heat of formation calculated with B3LYP,respectively.

参数α和γ分别控制S形函数Siga(v)和Sigb(v)的陡度,β是控制Sigb(v)弯曲程度的参数.Wij是连接输入层和隐藏层的突触权重,是连接隐藏层和输出层的突触权重(i=0-6,j=0-8,0代表输入层和隐藏层的偏置量项).

2 结果与讨论

采用B3LYP/6-311+G(3df,2p)计算56个物种的AE、42个物种的IP、8个物种的PA、10个物种的TAE以及180个物种的ΔfH⊖,计算结果与实验结果间的均方根偏差分别为12.6、20.5、6.7、43.1和50.2 kJ·mol-1(见表1).

训练集中每一个分子或原子的物理描述符gs、Ne、D、Ek、Q和ZPE的值从输入层输入神经网络,输出层得到修正的三参数新的三参数用于构建新B3LYP泛函,然后再将新B3LYP泛函用于计算AE、IP、PA、TAE和ΔfH⊖.这些值再同训练集中各物种的能量值进行比较以调整突触权重{Wij}和.最优化的突触权重值显示在表2中.

在xi=0.5(i=1-6)和x0=1(偏置量)时对xi(i=0-6)的导数值列于表3中,其值的大小反映了相应物理描述符对确定值的贡献,该数值越大,相应的物理描述符对确定ã0、ãx和ãc的值越重要.我们发现gs、Ne、D、Ek和Q对ã0、ãx和ãc的贡献都很大,这与文献[11]中选用的描述符相同,说明我们选择的描述符比较合适.因此,gs、Ne、D、Ek和Q被认为是五个最重要的物理描述符以确定ã0、ãx和ãc.训练集中所有的分子、原子和相关离子ã0、ãx和ãc的平均值是0.728、0.685和0.852,这不同于使用有限基组得到的初始B3LYP三参数值.对于训练组中每一个分子或原子而言,ãx＜ã0＜ãc始终成立,更重要的是,ã0、ãx和ãc的值彼此之间略有差异.即:相应的B3LYP泛函是系统相关的.

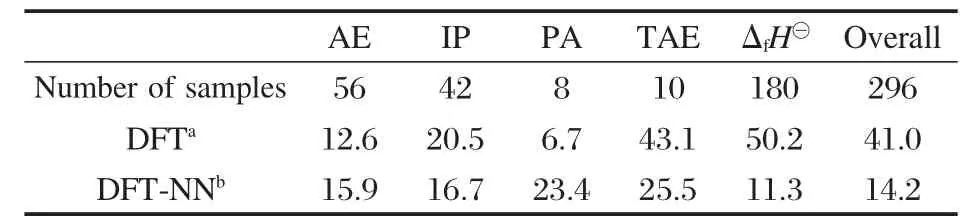
表1 神经网络修正前后的均方根偏差Table 1 RMS errors before and after the neural network correction

表2 最优化的突触权重Wij和Table 2 Optimized synaptic weightages Wijand jk

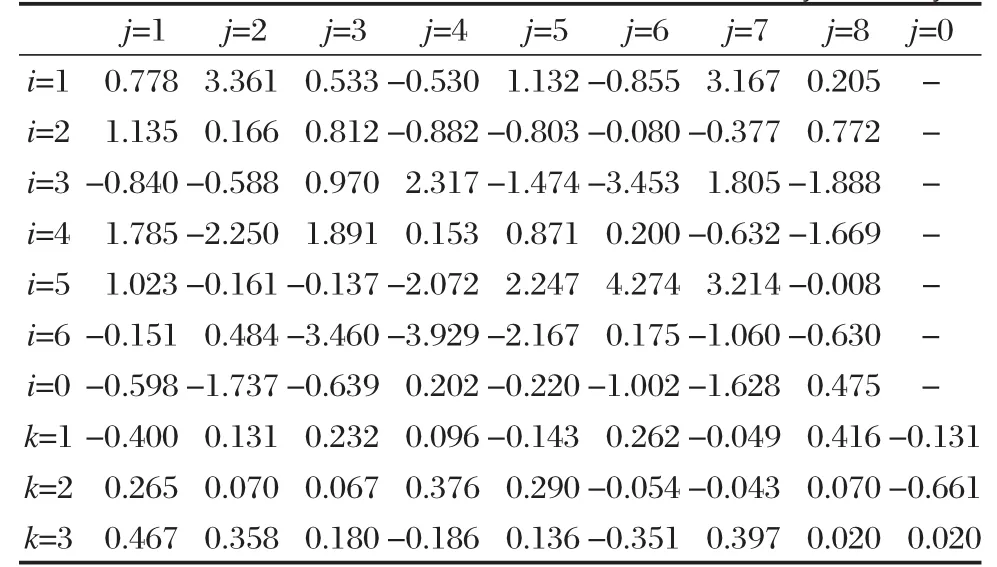
表2 最优化的突触权重Wij和Table 2 Optimized synaptic weightages Wijand jk

i=0-6:for bias and input neurons;j=0-8:for bias and hidden neurons; k=1-3:for modified three parameters in output layer

j=1 j=2 j=3 j=4 j=5 j=6 j=7 j=8 j=0 i=1 0.778 3.361 0.533-0.530 1.132-0.855 3.167 0.205 -i=2 1.135 0.166 0.812-0.882-0.803-0.080-0.377 0.772 -i=3-0.840-0.588 0.970 2.317-1.474-3.453 1.805-1.888 -i=4 1.785-2.250 1.891 0.153 0.871 0.200-0.632-1.669 -i=5 1.023-0.161-0.137-2.072 2.247 4.274 3.214-0.008 -i=6-0.151 0.484-3.460-3.929-2.167 0.175-1.060-0.630 -i=0-0.598-1.737-0.639 0.202-0.220-1.002-1.628 0.475 -k=1-0.400 0.131 0.232 0.096-0.143 0.262-0.049 0.416-0.131 k=2 0.265 0.070 0.067 0.376 0.290-0.054-0.043 0.070-0.661 k=3 0.467 0.358 0.180-0.186 0.136-0.351 0.397 0.020 0.020

表3 三个参数对各个描述符(xi)的导数Table 3 Derivatives ofwith respect to each physical descriptor(xi)

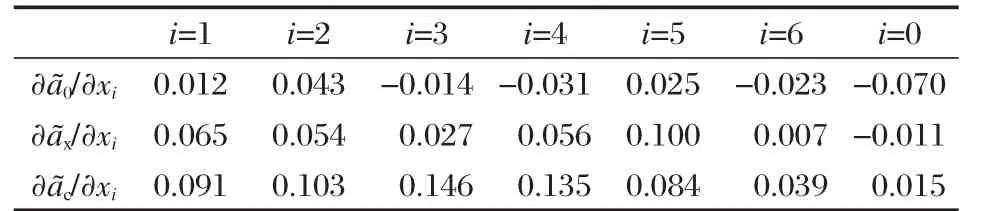
表3 三个参数对各个描述符(xi)的导数Table 3 Derivatives ofwith respect to each physical descriptor(xi)

i=0:for bias;i=1-6:for input neurons(gs,Ne,D,Ek,Q,and ZPE).

i=1 i=2 i=3 i=4 i=5 i=6 i=0∂ã0/∂xi 0.012 0.043 -0.014 -0.031 0.025 -0.023 -0.070∂ãx/∂xi 0.065 0.054 0.027 0.056 0.100 0.007 -0.011∂ãc/∂xi 0.091 0.103 0.146 0.135 0.084 0.039 0.015

为了检验神经网络的性能,我们从原有数据库中随机抽取了50个数据作为测试组,用以对确定的神经网络进行测试.测试组不同于训练组中的分子或原子,它主要用于对神经网络的性能进行检测.在测试阶段神经网络可以测出任何新分子的ã0、ãx和ãc,因为神经网络结构和所有的突触权重已由前面的训练过程所确定.新分子物理描述符的值可以通过传统的B3LYP计算得到,然后输入最优神经网络的输入层,经神经网络修正的ã0、ãx和ãc在输出层给出.修正后的三参数用于构建新B3LYP泛函以计算体系的特定性质.测试组50个数据同实验值的均方根偏差为18.4 kJ·mol-1.

3 结 论

本文中,我们使用神经网络方法对B3LYP三参数进行校正,并借助神经网络构建新B3LYP泛函.采用gs、Ne、D、Ek、Q和ZPE作为神经网络的描述符,并且以246个能量数据作为训练集以确定神经网络的结构和突触权重值.新的突触权重用于构建新B3LYP泛函,新B3LYP泛函再用于预测分子的性质.通过采用B3LYP/6-311+G(3df,2p)和B3LYP/ 6-311+G(3df,2p)-NN方法分别计算56个AE、42个IP、8个PA、10个TAE以及180个ΔfH⊖,计算结果与实验结果间的均方根偏差分别为12.6、20.5、6.7、43.1和50.2 kJ·mol-1和15.9、16.7、23.4、25.5和11.3 kJ·mol-1,总的均方根偏差从41.0 kJ·mol-1减小到14.2 kJ·mol-1.此神经网络对AE和PA的结果不能有效修正,原因可能是数据库中生成热数据较多以及生成热数值原始偏差较大,但对IP、TAE和ΔfH⊖起到很好的修正作用,尤其是对于ΔfH⊖的修正效果更为明显.应用此神经网络可以有效地预测分子的ΔfH⊖,同时,此神经网络将数据库从116个扩大到296个,增大了此神经网络的应用范围.

1 Koch,W.;Holthausen,M.C.A chemist′s guide to density functional theory.2nd ed.Weinheim:Wiley-VCH,2001:117-188

2 Parr,R.G.;Yang,W.Density-functional theory of atoms and molecules.New York:Oxford University Press,1989:285-317

3 Cramer,C.J.Essentials of computational chemistry:theories and models.2nd ed.West Sussex:John Wiley&Sons Ltd.,2004:355-424

4 Hu,L.H.;Wang,X.J.;Wong,L.H.;Chen,G.H.J.Chem.Phys., 2003,119:11501

5 Ceperley,D.M.;Alder,B.J.Phys.Rev.Lett.,1980,45:566

6 Becke,A.D.Phys.Rev.A,1988,38:3098

7 Lee,C.;Yang,W.;Parr,R.G.Phys.Rev.B,1988,37:785

8 Perdew,J.P.;Wang,Y.Phys.Rev.B,1992,45:13244

9 Perdew,J.P.;Chevary,J.A.;Vosko,S.H.;Jackson,K.A.; Pederson,M.R.;Singh,D.J.;Fiolhais,C.Phys.Rev.B,1992,46: 6671

10 Becke,A.D.J.Chem.Phys.,1993,98:5648

11 Zheng,X.;Hu,L.H.;Wang,X.J.;Chen,G.H.Chem.Phys.Lett., 2004,390:186

12 Curtiss,L.A.;Raghavachari,K.;Trucks,G.W.;Pople,J.A. J.Chem.Phys.,1991,94:7221

13 Curtiss,L.A.;Raghavachari,K.;Redfern,P.C.;Pople,J.A. J.Chem.Phys.,1997,106:1063

14 Jung,D.;Chen,C.J.;Bozzelli,J.W.J.Phys.Chem.A,2000,104: 9581

15 Chen,C.C.;Lay,T.H.;Bozzelli,J.W.J.Phys.Chem.A,2003, 107:6451

16 Sabzyan,H.;Omrani,A.J.Mol.Struct.-Theochem,2005,713:43

17 Duan,X.M.;Song,G.L.;Li,Z.H.;Wang,X.J.;Chen,G.H.;Fan, K.N.J.Chem.Phys.,2004,121:7086

18 Duan,X.M.;Li,Z.H.;Hu,H.R.;Song,G.L.;Wang,W.N.;Chen, G.H.;Fan,K.N.Chem.Phys.Lett.,2005,409:315

19 Yan,G.K.;Li,J.J.;Li,B.R.;Hu,J.;Guo,W.P.J.Theor.Comput. Chem.,2007,6:495

20 Hu,L.H.;Wang,X.J.;Wong,L.H.;Chen,G.H.J.Chem.Phys., 2003,119:11501

21 Wang,X.J.;Wong,L.H.;Hu,L.H.;Chan,C.Y.;Su,Z.M.;Chen, G.H.J.Phys.Chem.A,2004,108:8514

22 Duan,X.M.;Li,Z.H.;Song,G.L.;Wang,W.N.;Chen,G.H.; Fan,K.N.Chem.Phys.Lett.,2005,410:125

23 Zhao,J.;Cheng,X.L.;He,B.;Yang,X.D.Struct.Chem.,2006, 17:501

24 Li,H.;Shi,L.L.;Zhang,M.;Su,Z.;Wang,X.J.;Hu,L.H.;Chen, G.H.J.Chem.Phys.,2007,126:144101

25 Wu,J.;Xu,X.J.Chem.Phys.,2007,127:214105

26 Kohn,W.;Sham,L.J.Phys.Rev.A,1965,140:1133

27 Vosko,S.H.;Wilk,L.;Nusair,M.Can.J.Phys.,1980,58:1200

28 Perdew,J.P.;Kurth,S.;Zupan,A.;Blaha,P.Phys.Rev.Lett., 1999,82:2544

29 Perdew,J.P.;Kurth,S.;Zupan,A.;Blaha,P.Phys.Rev.Lett., 1999,82:5179

August 4,2009;Revised:October 17,2009;Published on Web:November 24,2009.

Neural Network Approach for a New B3LYP Functional with an Enlarged Training Set

ZHANG Jia-Hu WANG Xiu-Jun*
(Department of Applied Chemistry,College of Chemistry and Chemical Engineering,South China University of Technology, Guangzhou 510640,P.R.China)

A neural network approach was used to correct three parameters(a0,ax,and ac)in the B3LYP method for constructing a new B3LYP exchange correlation functional.A three-layer architecture which consisted of an input layer,a hidden layer,and an output layer,was adopted in the neural network.The total number of electrons,spin multiplicity,dipole moment,kinetic energy,quadrupole moment,and zero point energy were chosen as the most important physical descriptors.In this work,296 energy values were randomly divided into two subsets:246 energy values were used as the training set to determine the optimized structure of the neural network and the optimized synaptic weights;50 energy values were used as a testing set to test the prediction capability of our neural network. Three modified parameters ã0,ãx,and ãcthat were obtained from the output layer were used to calculate thermochemical data such as the atomic energy(AE),ionization potential(IP),proton affinity(PA),total atomic energy (TAE),and standard heat of formation(ΔfH⊖).The new results obtained,based on the neural network approach,are much better than the results calculated using the conventional B3LYP/6-311+G(3df,2p)method.Upon the neural network correction,the overall root-mean-square(RMS)error for the 296 species decreased from 41.0 to 14.2 kJ·mol-1.

B3LYP functional;Neural network; Descriptor; Training set

O641

*Corresponding author.Email:xjwangcn@scut.edu.cn;Tel:+86-20-87112945.

The project was supported by the National Natural Science Foundation of China(20975040).

国家自然科学基金(20975040)资助项目