N2O分子C1Π态的吸收光谱及解离动力学
甄 承 胡亚华 刘世林 周晓国
(合肥微尺度物质科学国家实验室(筹),中国科学技术大学化学物理系,合肥 230026)
N2O分子C1Π态的吸收光谱及解离动力学
甄 承 胡亚华 刘世林 周晓国*
(合肥微尺度物质科学国家实验室(筹),中国科学技术大学化学物理系,合肥 230026)
通过四波混频差频的方法产生高分辨的真空紫外激光,用以测量143.6至146.9 nm范围内的射流冷却N2O分子吸收光谱,对应于C1Π←X1Σ+的吸收跃迁.谱图显示出三个分立的振动谱峰叠加在宽吸收背景上,谱峰间隔分别是521和482 cm-1.前人的高精度量子化学计算表明C1Π态在N—O键长方向表现为无势垒的排斥态,而在N—N键伸缩及N2O弯曲振动方向则表现为束缚态,因此观测到的振动谱峰被归属为激发态的Feshbach共振.通过反Fourier变换可以得到Feshbach共振对应的非稳定周期轨道的特征周期为61 fs,相应的振动频率为546 cm-1.鉴于这一频率与弯曲振动频率非常接近,非稳定周期轨道被认为是由C1Π态的弯曲振动与解离运动相互作用而形成的,N—N伸缩振动没有参与形成非稳定周期轨道.由此,N2O分子C1Π态光激发-解离过程得以清晰地阐述.
吸收光谱;一氧化二氮;真空紫外光;解离
作为一种温室气体,N2O分子在燃烧化学和大气化学中有着重要的地位[1,2].当吸收真空紫外光后, N2O分子会发生光解,生成解离产物O(1D)原子,而O(1D)原子不仅在臭氧层的自然循环过程中起着关键的作用,而且还常被用作实验室研究相关化学反应动力学中激发态氧原子的来源[3-5].N2O分子的吸收光谱覆盖紫外区到真空紫外区,最红端位于240 nm附近,其中自160至220 nm的吸收带对应于B1Δ←X1Σ+的吸收[6],而自139到168 nm的吸收光谱,则被归属于N2O分子的C1Π←X1Σ+的吸收跃迁[7-9],此时N2O分子的解离原子碎片以O(1S)和O(1D)为主[10,11].值得注意的是,这两段吸收光谱的结构均表现为分立谱峰叠加在宽的连续背景上.早期的理论研究描述了N2O分子各电子态势能面的基本特征[12],其中B1Δ态是典型的预离解态,其平衡键角相对基电子态(线性分子)有很大的变化,同时在N—O键长方向存在一个低的解离势垒.最近的激发态量子波包计算[13]证实了B1Δ态的势能面特征,获得的B1Δ态吸收截面与实验结果非常吻合,而吸收光谱的分立谱峰被归属为Feshbach共振[14].
相对而言,N2O分子C1Π态的实验和理论结果则相去甚远.早期的实验研究中,Duncan[7]将观测到的C1Π态分立谱峰指认为N2O分子的弯曲振动,而Zelikoff等[8]则将分立结构归属为N2O分子的对称伸缩振动序列.事实上,由于当时缺乏C1Π态的分子结构和势能面信息,这些光谱归属具有很大的随意性.早期的量子化学计算[12]表明C1Π态在N—O键长方向表现为无势垒的排斥态.由此,C1Π态吸收光谱被预测为无结构的连续谱带,但这无法解释实验中观测到的分立谱峰结构.最近,Daud等[15]应用高精度的完全活性空间自洽场计算(CASSCF)和多参考态组态相关计算(MRCI)方法计算了N2O分子各电子态的势能面、吸收截面及解离产物的量子态布居,结果显示尽管N2O分子的C1Π态在N—O键长方向是排斥的,但其Franck-Condon区域内分子势能下降平缓,同时弯曲振动在激发过程非常有利(基态是线性,而激发态为弯曲构型).这样,吸收光谱中的分立谱峰则有可能来源于解离过程中弯曲振动与N—O键断裂相互竞争形成解离过渡态的振动激发(类似于B1Δ态的Feshbach共振).
为了在实验上验证这样的猜测,必须首先得到清晰的振动分辨吸收光谱,尽可能去除热带及谱带重叠的影响,从而通过光谱在频域上的反Fourier变换计算其自相关函数谱,得到Feshbach共振对应的非稳定周期轨道的特征周期.当前的研究中,我们在射流冷却条件下重新测量了N2O分子在143.6至146.9 nm范围内的吸收光谱,由于充分的振转温度冷却,获得的光谱极大地降低了热带的影响.通过反Fourier变换得到非稳定周期轨道的特征周期,由此我们不仅能够指认N2O分子C1Π态吸收光谱中分立谱峰结构的来源,而且还可以获得分子解离动力学过程的微观描述.
1 实验装置和原理
1.1 实验装置
当前的实验装置主要包括射流冷却的分子束系统、脉冲真空紫外光(VUV)源、真空紫外光吸收的检测系统,其中激光与分子束间的时间延迟由脉冲发生器(DG535,Stanford Research Systems,USA)控制.具体细节详见文献[16-18].
脉冲真空紫外光由四波混频差频(ωVUV=2ω1-ω2)过程产生.具体操作为,一台Nd∶YAG激光器(Lab-190-10,10 ns,Spectra-Physics,USA)的三倍频光(355 nm)经分束镜分为两束后,分别泵浦两台染料激光器(PRLC-LG-18和PRLC-LG-24,Sirah,Germany),输出的两束染料激光在混频池中聚焦重合.在当前的实验中,Kr气作为非线性介质,固定一束染料激光波长在Kr原子的(4p)5(2P3/2)5p,[1/2]0←(4p)6,1S0的双光子共振吸收峰处(2ω1=94093.66 cm-1),扫描另外一束可见染料激光ω2从而获得可调谐的脉冲真空紫外激光,其单脉冲激光能量约为0.1 μJ·pulse-1[17].输出的激光经分光室内的LiF棱镜(15°)分光,只选择允许VUV光进入吸收区,与超声射流分子束作用.
实验中,前滞压强为1.2×105Pa的N2O气体经脉冲喷嘴射入真空腔体,在下方5 mm处与VUV激光相互作用.为了增加分子束对光的吸收长度,采用狭缝喷嘴(0.1 mm×10 mm,General Valve,USA)使气束沿激光传播方向压扁拉长至约10 mm.真空室的动态真空是1.0×10-2Pa.为了准确测量脉冲VUV激光的线宽和分子束的冷却温度,在N2O气体中掺入体积分数为5%的CO气体,通过检测CO的A1Π←X1Σ+的激光诱导荧光,测得当前的VUV激光的线宽约0.3 cm-1,对荧光谱的温度拟合得到射流冷却分子束的转动温度约为40 K.考虑到混合气体中N2O占绝大多数,CO的温度可以认为是整个分子束体系的转动温度.实验中使用的N2O和CO气体均由南京特种气体厂提供,纯度分别是99.8%和99.9%.气体在实验前没有进一步纯化.
为了直接获得吸收光谱,沿光传播路径在光与分子束作用前后各放置一个LiF平板,将约5%的VUV光反射进入两个相同型号的光电倍增管(9403B, Electron Tubes,UK),从而同时监测吸收前后的激光光强.光电倍增管输出的电信号经数字示波器平均后,由计算机记录处理.
1.2 吸收光谱的测量原理
分子束对光的吸收遵循Beer-Lambert定律:

其中Il(λ)和I0(λ)分别为透射光强和入射光强,N、σ(λ)和l分别为分子的数密度、吸收截面和吸收程.此外,尽管两个光电倍增管型号完全相同,但是其对输入光强的响应仍会存在差别.采用参比实验的方法可消除这种影响,即当不打开喷嘴进行空扫时,前后光电倍增管获得的光强分别以和表示,这样真实的吸收光谱强度S(λ)可由下式表示:
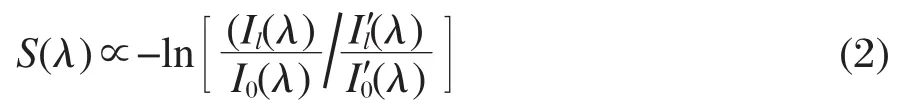
显然,由于(2)式中各光电倍增管记录的光强分别以比例出现,这样两个光电倍增管对光强响应的差别可以得到消除.
2 结果与讨论
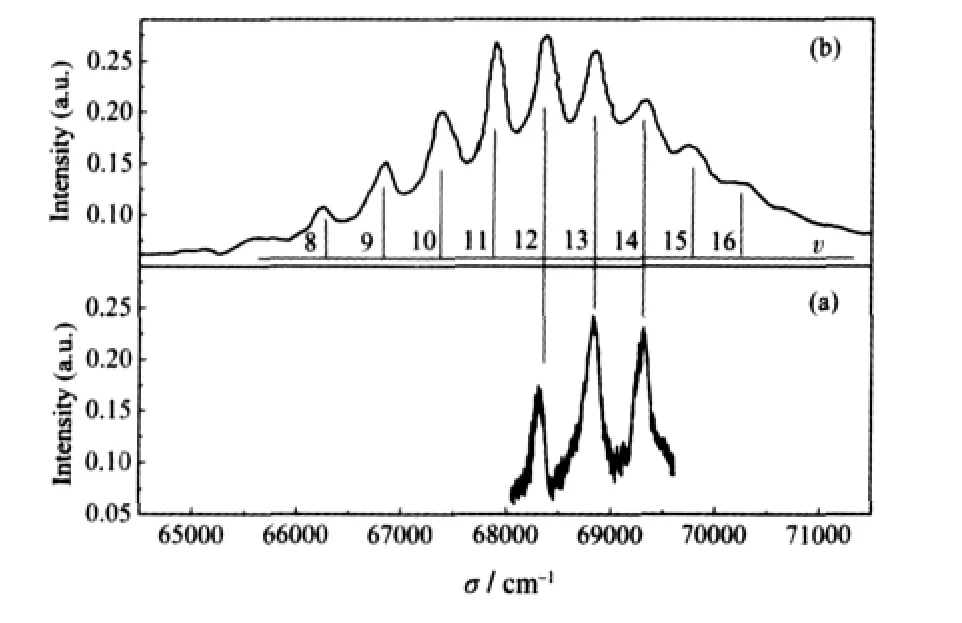
图1 不同实验条件下N2O分子C1Π←X1Σ+的吸收光谱Fig.1 Absorption spectra of the C1Π←X1Σ+transition of N2O measured at different experimental conditions(a)with the jet-cooled molecular beam;(b)in a flowing absorption cell at room temperature measured by Nee et al.[9],and assignment of the resonance peaks are shown as Nee et al.used in Ref.[9].
射流冷却的N2O分子在143.6-146.9 nm范围内的吸收光谱如图1(a)所示(能量范围是68050-69620 cm-1),最近Nee等[9]在气室中采用同步辐射光源测量得到的64500-71500 cm-1范围的吸收光谱如图1(b).尽管受限于染料波长,当前的实验光谱没有覆盖更多的波长范围,但是当前的吸收图与前人的实验工作基本一致,只是三个振动峰的相对强度明显不同.考虑到图1(b)的测量中存在大量的热带激发和转动激发,谱峰重叠非常严重,而当前的吸收实验中由于采用射流冷却,分子束温度约40 K,转动激发引起的谱峰重叠几乎不存在,同时热带激发也得到了有效的抑制,从而使得振动峰的相互重叠得到有效削弱,各振动峰的强度相对独立,因此当前的吸收谱较Nee等的结果显示出更为清晰的振动谱带结构,同时振动峰强度也有所差异.总体而言,在68050-69620 cm-1能量范围内,N2O分子的吸收光谱表现为三个非对称的分立振动谱峰叠加在宽的吸收背景上,两振动谱峰间隔分别是521和482cm-1.
理论计算[12,15]表明N2O分子C1Π态是典型的排斥态,可以解离生成NO和O(1D)原子.通常,这样的排斥态对应的吸收光谱表现为无振转结构的宽带.然而,实验中却清楚地观测到分立的振动谱峰.如前所述,理论计算的势能面[15]表明,这样的吸收谱峰结构可能是由于C1Π态的Feshbach共振导致的.具体而言,N2O分子C1Π态的弯曲振动或N—N伸缩振动在解离过程中与N—O键的断裂相互竞争,从而形成一个非稳定的周期轨道,即分子由基电子态被激发到排斥的上电子态时,波包从Franck-Condon区向周围随机扩散,其中绝大部分波包沿着解离方向运动,促使分子快速离解,然而有少部分波包则会沿着一些特殊的路径振荡运动(如N2O分子的弯曲振动模式或N—N伸缩振动模式),从而导致波包振荡回其初始位置附近,这样波包在向解离方向运动的同时也会沿这些路径振荡一个或者几个周期,形成吸收光谱中的分立结构谱峰.考虑到当前的激发能量范围是68050至69620 cm-1,远超过C1Π态的解离限,因此N2O弯曲振动或N—N伸缩振动所对应的非稳定周期轨道都可能导致吸收光谱的分立谱峰.
为证实以上猜测,同时也为确定非稳定周期轨道究竟来自N2O弯曲振动还是N—N伸缩振动,需要对测量的吸收光谱做适当处理和分析.由于分子电子态的吸收光谱与量子态波包在上电子态的动力学行为密切相关,其吸收截面σ(E)、激发能量E以及激发强度S(t)之间存在如下的反Fourier变换关系:
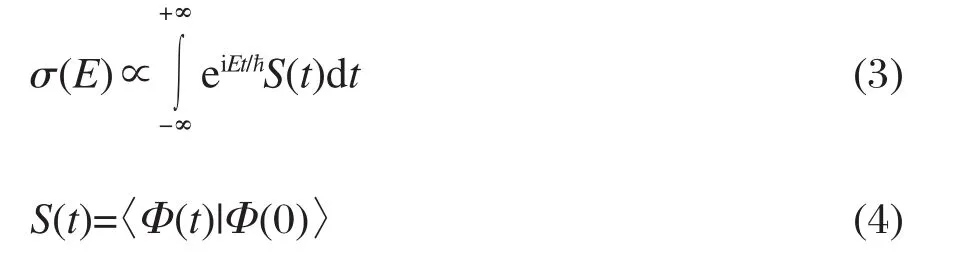
其中S(t)为自相关函数,Φ(0)为初始时刻上电子态的量子波包,Φ(t)则为t时刻上电子态的波包,ħ=h/ 2π,h为普朗克常数.这样,通过反Fourier变换分析可以得到对应时域的自相关函数S(t),其极大值将反映非稳定周期轨道的特征周期.类似的反Fourier变换分析曾被应用于CO2[19]、O3[20,21]和OCS[22,23]等分子体系的电子激发态解离动力学研究.图2显示在射流冷却条件下测量的N2O吸收光谱反Fourier变换结果.自相关函数S(t)在61 fs处出现极大值,这样就意味着N2O分子C1Π态存在着一个周期为61 fs的非稳定周期轨道.该振动周期对应频域的谱峰间隔为546 cm-1,接近实验观测到的谱峰间隔(521和482 cm-1).考虑到实验谱峰间隔是通过振动峰的最强处直接读取获得,而非对称谱峰形状及转动加宽等因素都会造成测量的误差,因此当前反Fourier变换得到的振动频率和实验测量的光谱间隔是基本一致的.
如前所言,N2O分子的C1Π电子态在N—O方向是直接解离的排斥态,因此理论计算没有给出振动频率.然而,Hopper[12]曾利用多组态自洽场MCSCF计算得到了N2O分子的各电子态在线性分子构型时的势能面.其中C1Π态势能曲面上,分子在N—N伸缩方向的Franck-Condon区域内C1Π态与基电子态的势能形状几乎完全一样,这样可以预见C1Π态的N—N伸缩振动频率应该与基电子态非常接近,约为1284.903 cm-1[24].遗憾的是,迄今为止C1Π态弯曲振动频率未见报道,而X1Σ+基电子态和B1Δ态的弯曲振动频率分别是588.768 cm-1[25]和589.61 cm-1[26].显然,尽管X1Σ+态和B1Δ态的平衡键角差别很大[15],但其弯曲振动频率则非常接近.考虑到B1Δ态和C1Π态的键角变化势能曲线的斜率比较接近[15],则C1Π态的弯曲振动频率应该也约为580 cm-1.由前面的反Fourier变换知道,当前观测到的非稳定周期轨道特征周期为61 fs,对应振动模式的频率为546 cm-1,远小于C1Π态N—N伸缩振动频率,却与预测的弯曲振动频率比较接近.这意味着观测到的非稳定周期轨道仅仅是由N2O弯曲振动与N—O键解离运动相互竞争形成的,而N—N伸缩振动则在光解离的过程中未参与形成非稳定周期轨道.
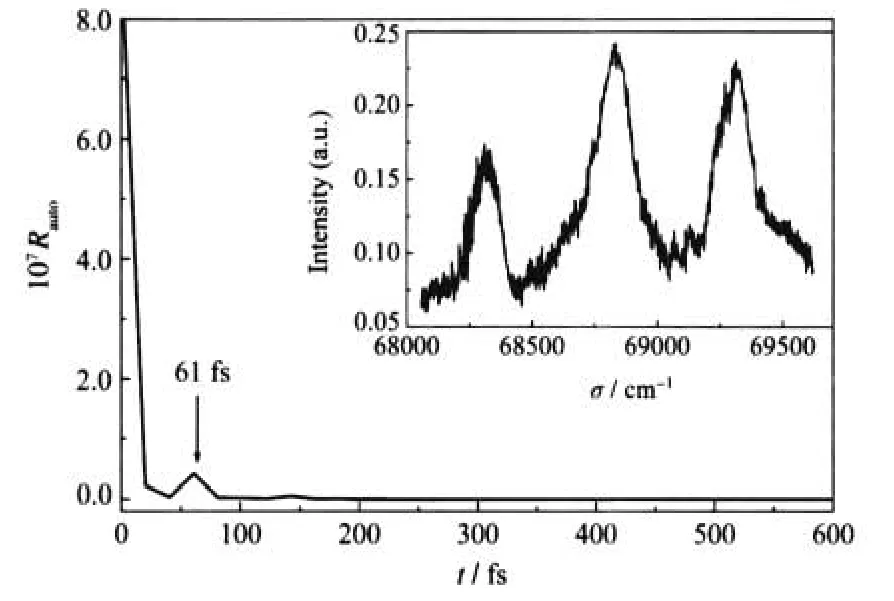
图2 射流冷却条件下N2O分子C1Π态吸收光谱的反Fourier变换得到的自相关函数Fig.2 Autocorrelation function obtained from the anti-Fourier transform of the absorption spectrum of the C1Π state of jet-cooled N2ORauto:autocorrelation;The corresponding absorption spectrum is shown in the insert panel as well.
进一步,考虑到当前实验光谱所包含的能量范围很窄,仅涉及v=12-14三个振动谱峰(见图1),那么在整个C1Π态吸收光谱范围内,除了存在弯曲振动相关的非稳定周期轨道,N—N伸缩振动是否也会在解离过程中被激发呢?为此,我们以Nee[9]和Zelikoff[8]等的实验吸收光谱为对象,分别对光谱进行了反Fourier变换分析,两个结果完全一致.由于在低能量端Zelikoff等[8]的实验光谱细节更为清晰,这里以这个吸收光谱为例,其反Fourier变换结果如图3所示.显然,尽管由于振动谱峰的重叠和转动加宽非常严重,但是在包括了更多的振动谱峰后得到唯一的非稳定周期轨道的特征周期是66 fs,与射流冷却的吸收光谱得到的61 fs特征周期非常接近,这意味着在整个N2O分子C1Π态的吸收光谱中,分立的振动谱峰几乎完全是由波包沿弯曲振动相关的非稳定周期轨道振荡引起的.
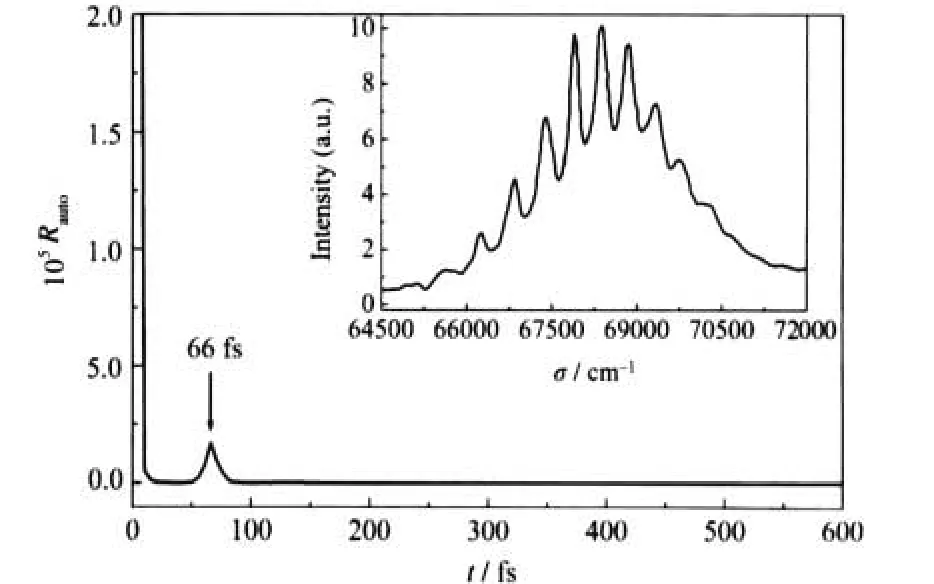
图3 室温下N2O分子C1Π态吸收光谱的反Fourier变换得到的自相关函数Fig.3 Autocorrelation function obtained from the anti-Fourier transform of the absorption spectrum of the C1Π state of N2O at room temperatureThe corresponding absorption spectrum comes from Ref.[8] and is shown in the insert panel as well.
由此,N2O分子C1Π态的光激发-解离过程得以清晰地描述.在吸收了一个真空紫外光子后,N2O分子被激发到C1Π电子态.由于C1Π态是排斥态,量子波包从Franck-Condon区向周围随机扩散,其中绝大部分波包沿N—O键长方向运动,使分子快速解离,同时有少部分波包则会沿着弯曲振动的模式来回振荡,从而导致波包回到其初始位置附近,这样波包在向解离方向运动的同时也会沿弯曲振动参与的非稳定周期轨道振荡一个或者几个周期,从而最终形成吸收光谱中的分立结构谱峰.也就是说,实验观测到的C1Π态吸收光谱的分立振动谱峰的来源与B1Δ态类似,均是由激发态的Feshbach共振引起的.
3 结 论
通过四波混频差频的方法在实验室产生高分辨的真空紫外激光,用以测量了68050至69620 cm-1范围内的射流冷却条件下N2O分子的吸收光谱.该段吸收光谱对应于N2O分子C1Π←X1Σ+单光子吸收跃迁,谱图显示出三个分立的振动谱峰叠加在一个宽吸收背景上,谱峰间隔分别是521和482 cm-1.
前人的高精度量子化学计算表明C1Π态是典型的离解态,在N—O键长方向表现为无势垒的排斥态,而在N—N键伸缩及N2O弯曲振动方向则表现为典型的束缚态.由此,N2O分子C1Π态吸收光谱中的分立振动峰被认为是激发态波函数在排斥态和束缚态的共同作用下沿非稳定周期轨道振荡解离的贡献.为确认非稳定周期轨道的来源,我们对当前的吸收光谱进行了由频域到时域的反Fourier变换分析,得到了唯一的非稳定周期轨道,其特征周期为61 fs,相应振动频率为546 cm-1,与观测的振动谱峰间隔一致.由于该振动频率值接近弯曲振动频率,因此当前的非稳定周期轨道被认为是由C1Π态的弯曲振动与解离运动相互作用而形成的,N—N伸缩振动则在分子解离过程中没有被激发.进一步,利用前人观测的C1Π态完整吸收光谱进行反Fourier变换,获得唯一非稳定周期轨道的特征周期为66 fs,与当前得到的61 fs特征周期非常接近,这意味着在N2O分子整个C1Π态的吸收跃迁中,N—N伸缩振动始终没有参与形成非稳定周期轨道,观测到的分立振动峰完全是由波包沿弯曲振动相关的非稳定周期轨道振荡引起的.
最终,我们得到了N2O分子C1Π态的光激发-解离过程的动力学图像:N2O分子被激发至C1Π电子态后,波包由Franck-Condon区向周围随机扩散,其中绝大部分波包沿N—O键长方向运动解离,而少部分波包则沿弯曲振动模式来回振荡,这种波包一边解离一边沿非稳定周期轨道振荡的动力学行为最终形成吸收光谱中的分立振动谱峰.
1 Wayne,R.P.Chemistry of atmospheres.Clarendon:Oxford,1991
2 Climate Change 1994;Radiative forcing of climate change and an evaluation of the IPCC 1992 IS92 emission scenarios.Houghton,J. T.;Filho,L.G.M.;Harris,N.B.Eds.Cambridge:Cambridge University Press,1995
3 Brouard,M.;Duxon,S.P.;Enriquez,P.A.;Simons,J.P.J.Chem. Phys.,1992,97:7414
4 Brouard,M.;Lambert,H.M.;Short,J.;Simons,J.P.J.Phys. Chem.,1995,99:13571
5 Alexander,A.J.;Aoiz,F.J.;Brouard,M.;Burak,I.;Fujimura,Y.; Short,J.;Simons,J.P.Chem.Phys.Lett.,1996,262:589
6 Leifson,S.W.Astrophys.J.,1926,63:73
7 Duncan,A.B.F.J.Chem.Phys.,1936,4:638
8 Zelikoff,M.;Watanabe,K.;Inn,E.C.Y.J.Chem.Phys.,1953, 21:1643
9 Nee,J.B.;Yang,J.C.;Lee,P.C.;Wang,X.Y.;Kuo,C.T.Chin.J. Phys.,1999,37:172
10 Young,R.G.;Black,G.;Slanger,T.G.J.Chem.Phys.,1968,49: 4769
11 Black,G.;Sharpless,R.L.;Slanger,T.G.;Lorents,D.C.J.Chem. Phys.,1975,62:4266
12 Hopper,D.G.J.Chem.Phys.,1984,80:4290
13 Nanbu,S.;Johnson,M.S.J.Phys.Chem.A,2004,108:8905
14 Feshbach,H.Ann.Phys.,1958,5:357
15 Daud,M.N.;Balint-Kurti,G.G.;Brown,A.J.Chem.Phys.,2005, 122:54305
16 Li,Q.F.;Wang,H.;Shi,Y.;Dai,J.H.;Liu,S.L.;Yu,S.Q.;Ma, X.X.Chin.J.Chem.Phys.,2004,17:333 [李奇峰,汪 华,石 勇,戴静华,刘世林,俞书勤,马兴孝.化学物理学报,2004, 17:333]
17 Li,Q.F.;Wang,H.;Yu,Y.Q.;Liu,S.L.;Yu,S.Q.;Ma,X.X. Chin.J.Chem.Phys.,2005,18:474 [李奇峰,汪 华,喻远琴,刘世林,俞书勤,马兴孝.化学物理学报,2005,18:474]
18 Hu,Y.H.;Zhen,C.;Dai,J.H.;Zhou,X.G.;Liu,S.L.Chin.J. Chem.Phys.,2008,21:415
19 Schinke,R.;Engel,V.J.Chem.Phys.,1990,93:3252
20 Johnson,B.R.;Kinsey,J.L.Phys.Rev.Lett.,1989,62:1607
21 Johnson,B.R.;Kinsey,J.L.J.Chem.Phys.,1989,91:7638
22 Yamanouchi,K.;Ohde,K.;Hishikawa,A.;Pibel,C.D.Bull.Chem. Soc.Jpn.,1995,68:2459
23 Hishikawa,A.;Ohde,K.;Itakura,R.;Liu,S.L.;Yamanouchi,K.; Yamashita,K.J.Phys.Chem.A,1997,101:694
24 Toth,R.A.J.Opt.Soc.Am.B,1986,3:1263
25 Jolma,K.;Kauppinen,J.;Horneman,V.M.J.Mol.Spectrosc., 1983,101:278
26 Toth,R.A.Appl.Opt.,1991,30:5289
September 17,2009;Revised:October 30,2009;Published on Web:December 4,2009.
Absorption Spectrum and Dissociation Dynamics of the C1Π State of N2O
ZHEN Cheng HU Ya-Hua LIU Shi-Lin ZHOU Xiao-Guo*
(Hefei National Laboratory for Physical Sciences at the Microscale,Department of Chemical Physics, University of Science and Technology of China,Hefei 230026,P.R.China)
The absorption spectrum of the N2O molecule in the wavelength range of 143.6-146.9 nm was measured under the jet-cooled condition by using the high resolution vacuum ultraviolet radiation,which was generated by resonance-enhanced difference-frequency mixing,corresponding to the C1Π←X1Σ+transition.Three vibrational bands were observed with frequency intervals of 521 and 482 cm-1,and they were superimposed on a wide absorption background.Previous high-level quantum chemical calculations indicate that the C1Π state of N2O is dissociative along the N—O elongation,while it is bound along the N—N bond stretching or N2O bending.Therefore,the observed vibrational progression is a Feshbach resonance of the dissociative transition state.From an anti-Fourier transformation analysis,the recurrence period of the unstable periodic orbit of the Feshbach resonance was found to be 61 fs and the corresponding vibrational frequency was 546 cm-1.Since this vibrational frequency is close to the frequency of the bending motion,the unstable periodic orbit is mostly composed of the bending motion of the C1Π state coupled with dissociation.The N—N stretching vibration does not participate in its formation.Therefore,we describe the excitationdissociation dynamics of the C1Π state of N2O clearly.
Absorption spectrum;N2O;Vacuum ultraviolet;Dissociation
[Article] www.whxb.pku.edu.cn
*Corresponding author.Email:xzhou@ustc.edu.cn;Tel:+86-551-3600031;Fax:+86-551-3602323.
The project was supported by the National Natural Science Foundation of China(20533070,20603033),Natural Science Foundation of Anhui Province,China(070415214),and National Key Basic Research Program of China(973)(2007CB815204).
国家自然科学基金(20533070,20603033),安徽省自然科学基金(070415214)和国家重点基础研究发展规划项目(973)(2007CB815204)资助
O644;O643

