廓形不光滑螺旋面的加工铣刀刃形设计*

杨瑞军

(淮海工学院工程训练中心，江苏连云港 222005)

模具中出现的螺旋面，端面廓形一般是由一段或数段曲线(或曲线和直线)光滑连接构成，曲线(或直线)间的交接点处存在公切线，对应设计的铣刀刃形也是光滑连接的［1-2］。但对于某些特殊模具零件，构成其廓形的曲线和直线间交接点处无公切线，如图1所示，在直线de与外摆线cd间的交接点d处存在尖点。此时如按光滑连接来设计计算铣刀刃形，则求出的对应工件cd和de段的铣刀刃形12段和34段会出现刃形交错现象(图2a)，或刃形分离现象(图2b)。对于刃形交错的铣刀，由于无法在同一把铣刀上制造出交错刃形，即只能做出刃形1k和4k段，因而刀具上少了2k和3k两段刃形，故它无法铣出正确的表面。对于分离的铣刀刃形，为了防止尖点d被切掉，可以采用开凹槽的方法进行处理(图2c)。但开凹槽的刀刃上会产生2、3两个尖点，且2、3两尖点极易磨损，影响刀具的耐用度。还有假设延长工件廓形上的cd和de线段的办法，如图3a所示，以使铣刀的刃形相接(即不出现分离)。由于假设延长的部分在刀体的里边，即被铣刀切掉，因此该方法在理论上是行得通的。用这种方法设计的铣刀刃形会是图3b所示的情形，即铣刀的刃形由两段构成且2、3点并不相接，但是铣刀的制造还是很麻烦的。因此，只有消除刃形交错和分离，或求出分离部分的过渡刃形，才是解决问题的根本办法。

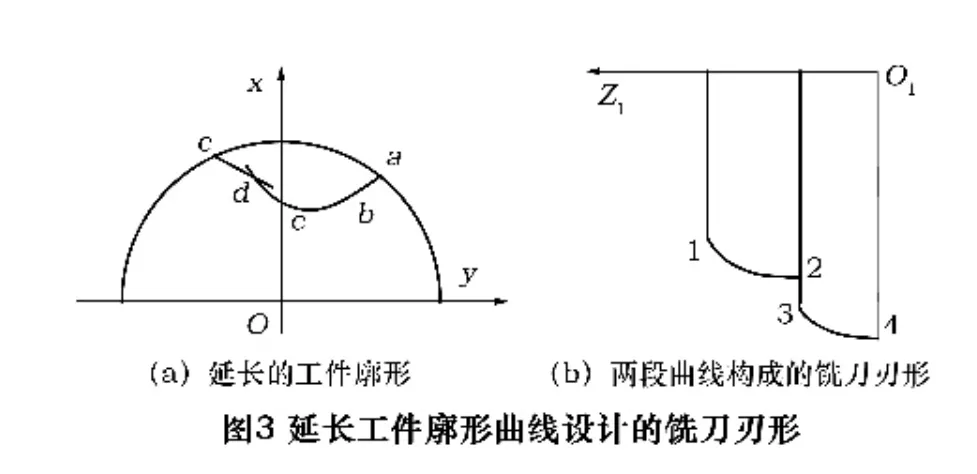
1 刃形交错和分离的成因

加工工件的螺旋面时，铣刀的回转表面与工件螺旋面在相对运动的任一瞬时，两表面之间总有一条相切的接触线。设计铣刀就是先求出接触线，然后使其绕刀轴线回转得到铣刀的回转表面［3］。以图1的工件为例，工件的左半侧廓形由de和cd段组成，交接点d为尖点，de和cd段曲线各自形成自己的螺旋面M和N，两面的交线就是尖点d形成的螺旋线D-D。按有关方法求出的接触线如图4a所示［4］，即接触线在M、N面上分别为e1d1和d2c1(d1、d2都在尖点形成的螺旋线D-D上)，相应的刀具截形为12和34，则铣刀刃出现刃形交错现象。如果铣刀与工件的接触线在M、N面上(如图4b所示)，则相应的刀刃形会出现分离现象。如果能适当改变刀具的安装参数，即改变刀具与工件轴线的最短距离A和轴交角δ(图5)，使M、N面上的接触线 e1d1和 d2c1相交于一点，即 d1和 d2点重合于螺旋线D-D上一点d，如图6所示。那么，相应的刀具截形也就相交于一点，这样就能保证刀具的设计不出现刃形交错和分离，此时过尖点螺旋线上d处的铣刀圆的切线与该点的螺旋线的切线重合。下面以此为条件来求解使铣刀刃形相接的条件式。

2 铣刀刃形相接的条件

2.1 圆柱螺旋面方程

螺旋面是由它的端截形或轴向截形作螺旋运动所形成的。设在空间有一固定坐标系O-xyz，其坐标轴方向的三个单位矢量分别为i、j、k。则已知的圆柱螺旋面工件端面廓形T的参数方程为

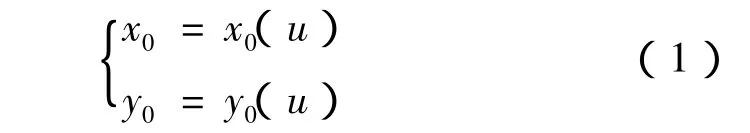
式中：u为参变量。

当端面廓形T绕z轴作等速转动，同时又沿z轴作等速移动时，曲线T在空间形成的轨迹曲面就是等升距圆柱螺旋面(简称为螺旋面)。如端面廓形T绕z轴转过θ角同时以导程Pz沿z轴上升Pzθ/(2π)时(如图7)，则形成的螺旋面方程用坐标式表示为

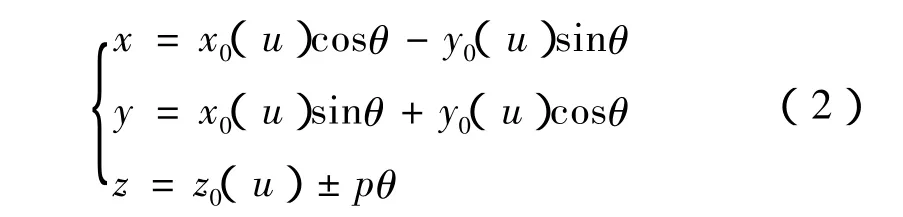
式中：θ为母线从起始位置绕z轴转过的角度，顺着z轴看，以顺时钟方向转动为正；p为螺旋参数，p=Pzθ/(2π)。式中±和∓号作这样规定：上面的用于右旋螺旋面，下面的用于左旋螺旋面。

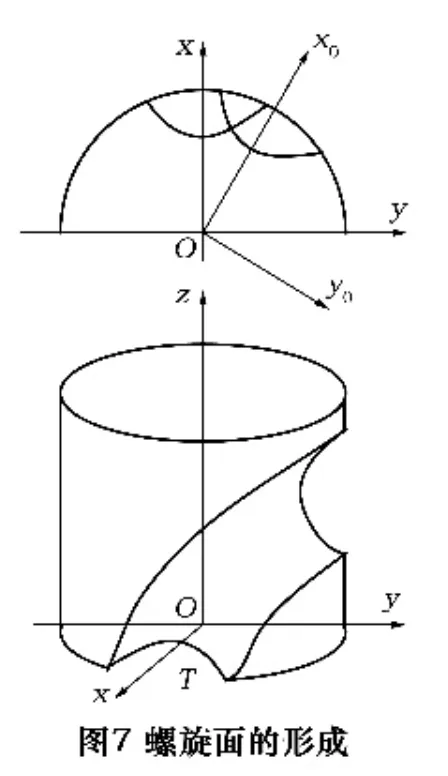
2.2 工件与刀具的坐标系

如图5所示，在工件上建立直角右手坐标系O-xyz，其中z轴与工件的轴线重合；在刀具上建立坐标系O1-x1y1z1，其中z1轴与刀具的轴线重合，x1轴与工件坐标系中的x轴重合。以上两个坐标系在空间位置是固定的，不随工件和刀具转动。

设刀具轴线与铣刀轴线的最短距离为A，以及两轴线间的夹角为δ，则由图5知，从O坐标系到O1坐标系的变换式为

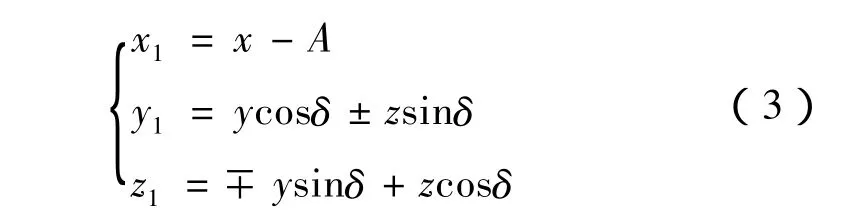
设坐标轴 x1，y1，z1方向的单位矢量为 i1、j1、k1，则单位基矢量间的变换式为

刀具回转面的轴向截形即刀具廓形方程为

2.3 铣刀刃形相接的条件式

设接触线在交接点d处的铣刀外圆半径为Rd(如图6)，则刀具d点处在O1坐标系中的铣刀圆方程为

其矢量方程为

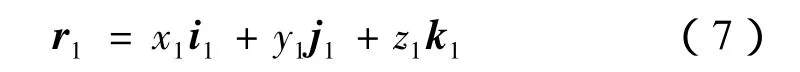
故铣刀圆在d点处的切矢为

将式(3)、(4)代入式(8)得 d 点刀的外圆切矢为

由式(2)代入上式化简得

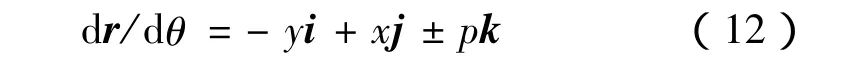
由过d点的铣刀圆切矢与过d点的螺旋线切矢平行的条件有如下关系式

将尖点d的端面截形坐标(x，y)代入式(13)即可求得使铣刀刃形相接的安装角δ和轴间距A。设计时，可考虑工艺条件和刀具设计的要求，选定出合适的最大铣刀圆半径以确定A，然后按式(13)求出此时使铣刀刃形相接的安装角δ。

3 铣刀分离部分的过渡刃形求解

当工件的端面齿形窄而深时，按式(13)修正后的δ角安装铣刀则会导致工件的外边缘部分过切掉(图8)。如采取缩小铣刀直径的方法来避免过切，会造成铣刀的直径太小无法正常设计。因此，最好的办法是精确求出铣刀上这部分分离的过渡曲线刃形，以保证尖点不致被切掉。

从图4b的分析可知，刀刃之所以出现分离是因为接触线在尖点形成的螺旋线D-D上的 d1、d2不重合的缘故。因而接触线e1d1和d2c1分别绕铣刀轴线回转一圈时形成的铣刀廓形出现了分离。因此，只要将d1d2段螺旋线求出，让其绕铣刀轴线回转一圈，即可求得铣刀分离部分的过渡曲线。当已知工件端面廓形的尖点d在O系中的坐标(X0，Y0)时，将其代入螺旋面的方程式(2)，即可得到尖点d形成的螺旋线D-D的方程为

d1d2只是尖点形成的螺旋线上的某一段曲线，要求出d1d2段的螺旋线，还必须确定θ的取值范围。为了确定式(14)中θ的取值范围，可求得接触线e1d1上对应点d1的角度参数θ1和d2c1上对应点d2的角度参数 θ2，显然，螺旋线 d1d2方程式(14)中 θ的取值范围为：θ1≤θ≤θ2。取不同的 θ 值即可由式(14)求得工件上一系列的接触点坐标，将其代入式(3)即可换算得到刀具上的接触点坐标。再由式(5)即可求得分离部分的刀具廓形。

［1］潘礼和，王春复.螺旋槽成型铣刀的加工［J］.工具技术，2007，41(9).

［2］吴卓，马世辉.加工螺旋槽成形铣刀的计算机辅助设计［J］.新技术新工艺，2009(4).

［3］张俊峰，王华震，左忠新.螺旋槽专用成型刀的设计与加工［J］.工具技术，2005，39(2).

［4］刘杰华.刀具精确设计理论与实践［M］.北京：国防工业出版社，2005：44-49.