Cr12模具钢铣削性能的研究*

陈孝光 王永国 刘 钢 李 明 姜良银 黄文鑫

(①上海大学机电工程与自动化学院，上海，200072；①上海工具厂有限公司，上海，200093；③机械工业高速精密工具工程技术研究中心，上海， 200093)

随着工业的高速发展以及生产水平的不断提高，具有高效率、低成本、节约原材料和产品质量好等特点的模具成型工艺越来越多地代替传统的切削加工工艺和其他加工工艺。如温拔、冷拔、精冲、冷挤压、冷弯、热挤压以及压铸工艺等，均已得到广泛应用。例如70%以上的汽车、拖拉机、电机、电器、仪表零件，80%以上的塑料制品，70%以上的日用五金等都是用模具成型的方法来生产的［1-2］。

模具制造过程中，需要提供很高的精度与加工效率，以达到现代工业的需求。机械加工作为模具加工过程中的通用性较好的加工方式被广泛应用［3-4］，铣削加工为机械加工中主要加工方式。模具铣削加工过程中，切削力的大小与进给量、切深、表面速度等切削条件有很大关系，且与刀具寿命有关并影响到工件的加工精度。而加工工件表面粗糙度是衡量已加工表面质量的重要指标。影响切削加工表面粗糙度的因素也很多，如切削加工条件、工件材料、机床振动、刀具参数以及产生的积屑瘤、鳞刺等。铣削表面粗糙度可以通过预测模型来预测［5］。

本文采用理论分析与切削试验相结合的方法分析研究了铣削Crl2模具钢时切削参数与切削力和表面质量的关系。

1 切削力实验研究

1.1 实验设计

本实验采用正交试验设计方法进行设计，对于Cr12槽铣与侧铣分别设计实验参数。以减少试验次数，有利于线性回归数学模型的建立。本文铣削的材料为Cr12淬硬模具钢，硬度为230 HB。

表1 试验加工条件

切削力实验在DMG公司生产的DECKEL MAHO DMU 50 evo linear五轴加工中心上进行。刀具采用上海工具厂生产的MG-4BA35M-D6-M1PCS，直径为6 mm的整体硬质合金TiN涂层立铣刀(图1)。

实验过程中的加工条件见表1。铣削力信号采集采用瑞士KISTLER 5070测力仪，构成如图2、3所示。

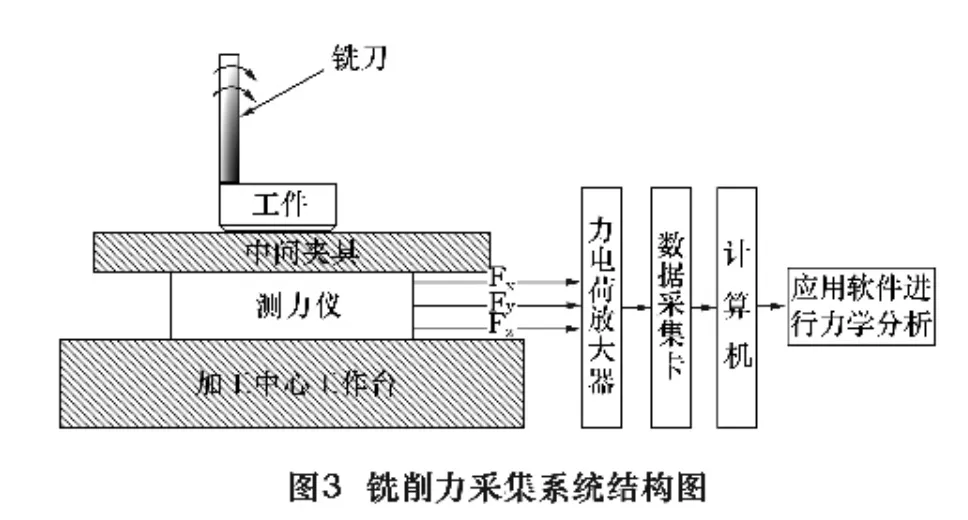
本试验分为槽铣与侧铣。采用正交试验方法设计三因素三水平与四因素三水平正交试验。切削参数如表2、表3所示。试验编号及对应参数分别见表4、表5。表中：Vc、fz、ap、ae、n、F 分别表示刀具线速度(m/min)、每齿进给量(mm/z)、轴向切深(mm)、径向切宽(mm)、转速(r/min)、进给速度(mm/min)。

表2 槽铣试验参数

表3 侧铣试验参数

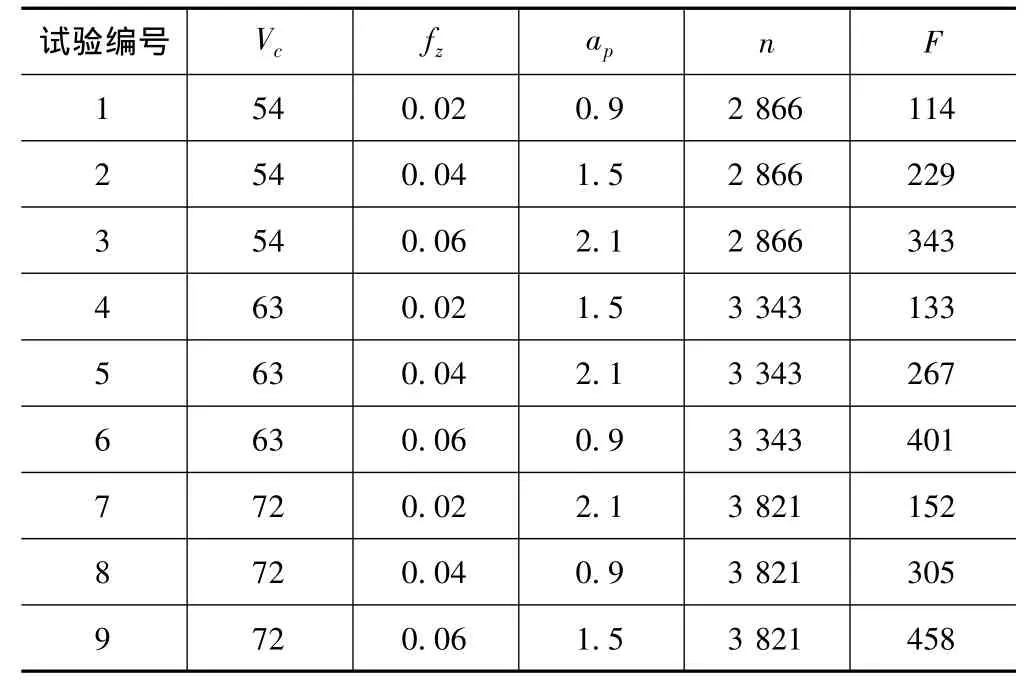
表4 槽铣正交试验设计参数(ae=d0)

表5 侧铣正交试验设计参数

1.2 实验结果

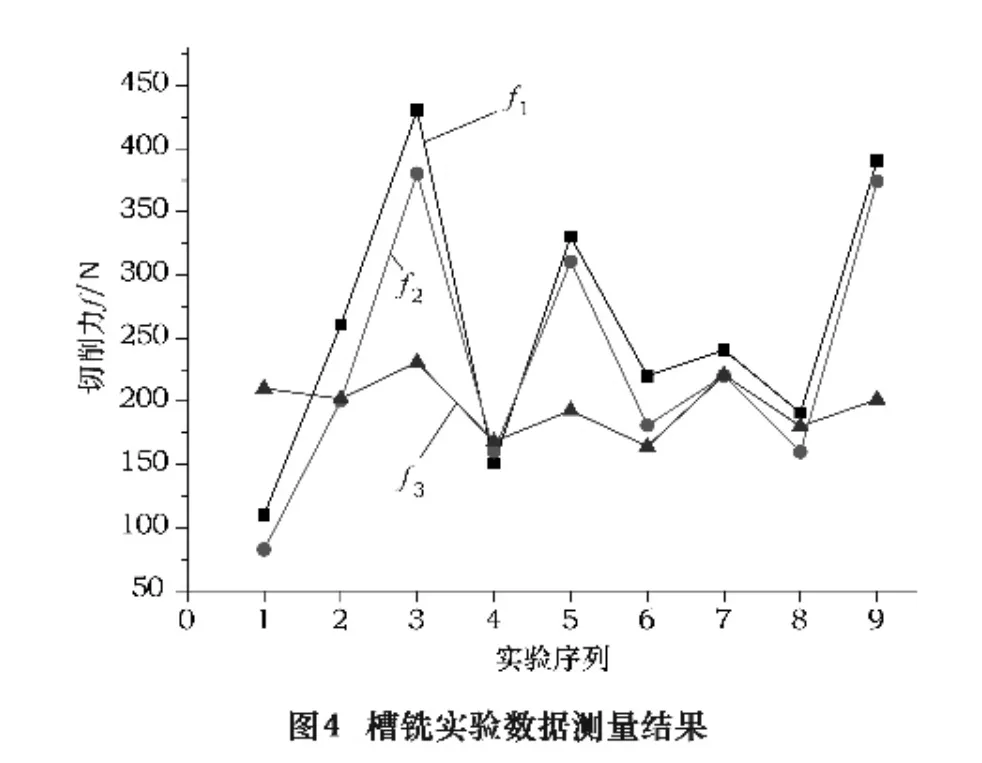
不同实验条件下槽铣和侧铣的切削力如图4、5，其中 f1、f2、f3分别为 x、y和 z向切削力。可以看出，对槽铣和侧铣，z向切削力f3基本上与加工参数无明显相关性，故而可以不考虑。而本研究中f2为主切削力，因而我们考虑f2与加工参数的变动关系建立铣削数学模型。记f2为Fz。

2 铣削力数学模型

本研究采用多元回归方法，分别用两种切削方式的结果来建立切削力与切削参数之间的关系模型。

在实践过程中，一般使用指数公式作为切削力的经验拟合公式，这种指数回归方程通常用于正交试验设计场合，适合本研究的使用。由金属切削原理可知，在机床、刀具和工件材料确定的情况下，铣削力Fz和铣削参数之间的关系可表示为［6］

其中变动参数为铣削深度ap，每齿进给量fz，铣削宽度ae和转速n。已知铣刀齿数z=4，铣刀直径d0=6 mm。由此得到其经验公式为

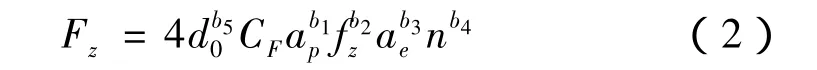
特别的，对于槽铣，经验公式为

以下为通过以上所述的公式以及实验得到的数据，应用多元线性回归的方法求得的切削力经验公式。

2.1 侧铣的铣削力数学模型

对式(2)进行线性化处理，即取对数。本研究中，刀具直径不变，得到

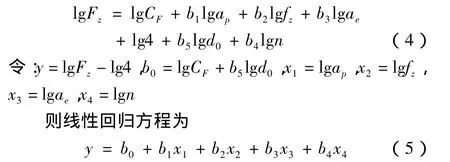
在式(5)中，b0、b1、b2、b3、b4为待求的 4 个数值；y、x1、x2、x3、x4分别取 n个不同的数值(本次试验中 n=9)。

对于线性方程(5)，n个试验点，各点的偏差为

应用多元线性回归的方法并利用Matlab将试验结果进行多元线性回归分析，通过最小二乘法对参数b0、b1、b2、b3、b4进行估计，从而得到主切削力 FZ与铣削深度ap、每齿进给量fz、铣削宽度ae、转速n之间的线性回归模型［7］。如下：

2.2 槽铣的铣削力数学模型

对于槽铣，由于其ae也为d0，为常数。因而可对式(5)进行化简。令b0=lgCF+b5lgd0+b3lgae，y=lgFzlg4，x1=lgap，x2=lgfz，x4=lgn，则上式(5)化为下式：

通过Matlab编程求出b0=-0.4617，b1=0.9491，b2=0.6535，b4=0.8454。得出方程为

3 铣削力实验结果分析

对于侧铣，通过最小二乘法计算得到 R2为92.5%，R越大，数据拟合得越好。F统计量值为12.375，取检验的显著水平为0.01，由F分布临界表(α=0.01)查得 F0.01(P，n-P-1) =12.06，则得到的回归方程是显著的。

回归方程呈显著性，但并不一定所有自变量对因变量的影响都显著，自变量对因变量的影响不显著说明二者之间关系呈非线性或者与二者无关［6］。所以要对回归系数进行显著性检验，以考察每个切削参数对切削力的显著程度。对假设 H0i：bi=0(i=1、2、3、4、5)进行检验，所用统计量为

取检验的显著水平为0.01，查表得t1-α/2(n-k-1)=t0.995(3)=5.8409，进行显著分析可得：

由回归系数显著性检验可知，对于Fz，影响显著性排序为：

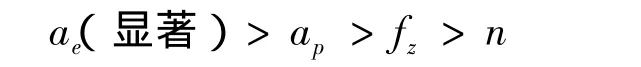
对于槽铣，铣削力的数学模型：R2=99.0%，F统计量值为160.593，取检验的显著水平为0.01，由F分布临界表(α =0.01)查得 F0.01(P，n-P-1) =15.98，则得到的回归方程是显著的，与实际情况拟合较好。

由回归系数显著性检验可知，对于Fz，影响显著性排序为：

4 粗糙度分析

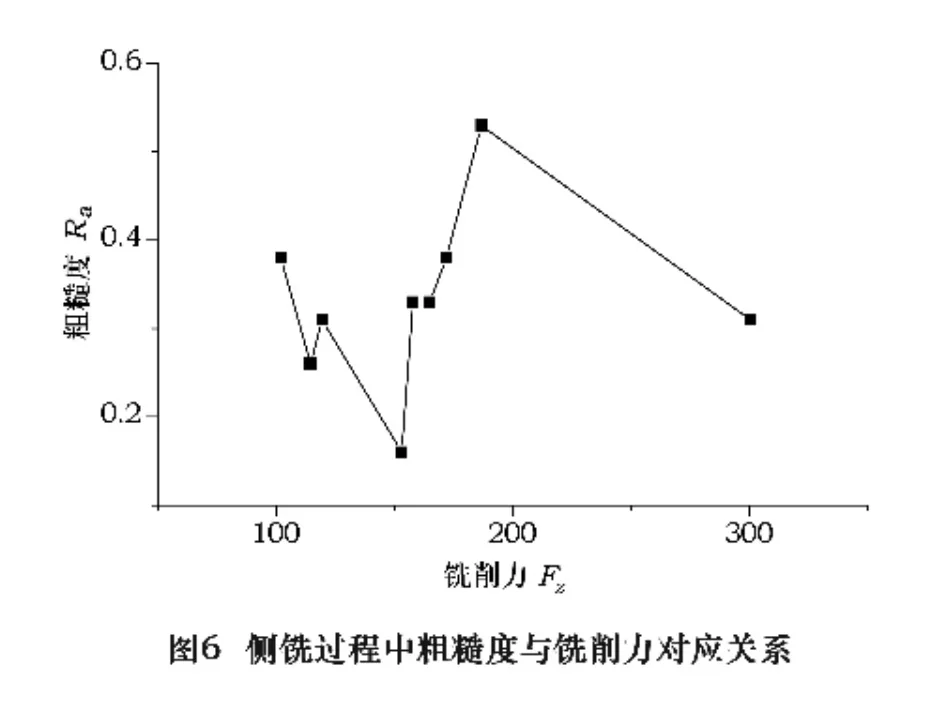
侧铣粗糙度数据如图6。可以得出：在对Cr12模具钢的侧铣过程中，粗糙度与铣削力并不是严格对应增减的，而是在不同区段呈不同特性。在Fz＜150 N的时候，其粗糙度稳定在Ra=0.2～0.5 μm之间；在Fz=150～220 N范围内，粗糙度与铣削力呈正相关关系。在Fz=150 N时候，Ra得到最小值。因而在该范围内，应尽量设法使铣削力减小。同时，在侧铣过程中，铣削力集中在Fz=150～220 N范围内。因而对于实际加工，若要减小粗糙度值，应该首先考虑减小切削力。

5 结语

在五轴加工中心上对Cr模具钢进行铣削试验，通过对加工条件与铣削力和表面粗糙度的关系进行分析，建立了数学模型，并通过一系列的分析，得出以下结论：

(1)在低速铣削段内，切削力大小与转速关系不明显。而与ae、ap有很大关系。要减小铣削力，提高加工表面质量，通过调整这些参数就可以达到目的。具体的调整方向与优先度为：增大ae，增大ap、提高fz、增大n(侧铣)或降低n(槽铣)。

(2)当铣削力较小时，表面粗糙度随切削参数的变化不大；当切削力超过一定范围后，表面粗糙度值则会明显增大。因而在精密切削时，考虑到加工质量，切削参数的选取必须保证其切削力Fz=(140～200)N。

(3)为了减小铣削过程中的铣削力，通过对文中的数学模型进行分析，本文给出的切削参数的推荐范围为：n=4000～5000 r/min，ae=0.5～0.8 mm，fz=0.08 ～0.12 mm/z，ap=4 ～6 mm。

［1］甄瑞麟，模具制造工艺学［M］.北京：清华大学出版社，2005.

［2］魏庆岐，国内外模具钢的概况［J］.河北冶金，1996(1)：42-45.

［3］赵国艳，赵晓明，许黎明.高速铣削加工中进给量和进给间隔对表面粗糙度的影响［J］.上海交通大学学报，2005，39(1)：108-103.

［4］吴卫国，王贵成，马利杰，等.精密车削Cr12模具钢的表面粗糙度研究［J］.工具技术，2007(41)：38-40.

［5］田欣利，佘安英.基于回归分析方法的铣削表面粗糙度预测模型的建立［J］.制造技术与机床，2008(11)：101-103.

［6］韩荣第，周明.金属切削原理与刀具［M］.哈尔滨：哈尔滨工业大学出版社，2007.

［7］王沫然.MATLAB与科学计算［M］.北京：电子工业出版社，2003.