一个新的非常规Hermite型矩形元的构造及收敛性分析

刘付军，卢 静

(1.河南工程学院 数理科学系，河南 郑州 451191；2.河南工程学院 计算机科学与工程系，河南 郑州 451191)

1 问题的提出

考虑下面的二阶椭圆方程，求u满足:

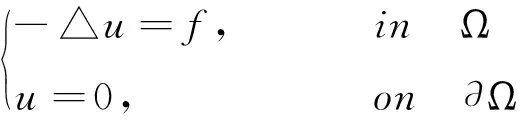
(1.1)

其中, Ω⊂R2是有界凸区域，f∈L2(Ω)是已知函数.令ψ=u，则问题(1.1)的混合变分形式为：求(ψ,u)∈H×M满足:

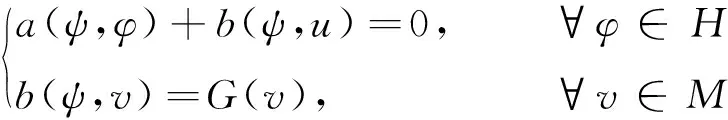
(1.2)

其中,H={φ∈L2(Ω)×L2(Ω),divφ∈L2(Ω)},m=L2(Ω);

如果Hh⊂H和Mh⊂M是混合有限元空间，则(1.2)的混合有限元解为：

求(ψh,uh)∈Hh×Mh满足:

(1.3)

这里先给定几个假设[1]，本文正是基于它们得到了一些结论：

(H1)D⊂H′×M′使得问题(1.2)存在唯一的解(ψ,u)∈H×M

(H2)存在Hilbert空间V使得M→V(连续嵌入)，并且使得对于∀d∈V′存在(λd,yd)∈H×M,满足:

(1.4)

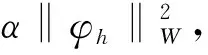
Zh={φh∈Hh；b(φh，vh)=0， ∀vh∈Mh}.

(H4)存在s(h)>0使得‖vh‖H≤s(h)‖vh‖w, ∀vh∈Mh.

(H5)存在算子rh∶Y→Hh使得对于任意的φ∈Y有b(φ-rhφ,vh)=0,∀vh∈Mh,其中Y={ψ,λd;d∈V′},ψ是问题(1.2)的解(ψ,u)中的ψ,λd是(1.4)中的解(λd,yd)中的λd.

利用混合有限元解Poisson方程最早是由Raviart-Thomas于1977年提出的[2-3].二十多年来，基本上都是使用这种格式，后续的一些工作都是在利用Raviart-Thomas格式去讨论稍微复杂的二阶椭圆方程,给出各种模的误差估计[4-7].但是,Raviart-Thomas所用的自由度太多而且论证过程也很复杂.此后，罗振东又采用一种自由度较少、论证过程也较简单的混合有限元格式[8-9],但是其研究的都是三角形单元.本文将利用由[10]改造得到的非常规Hermite型矩形元来研究二阶椭圆问题，并得到了其收敛性结果.

2 单元构造

为简单起见，设Ω是R2中的一个有界凸多边形区域，其边界∂Ω平行于x轴或y轴，h是Ω的一个矩形剖分族，即∀e∈h设其中心点为(xe,ye),两边分别平行于x轴和y轴,两边长分别为2hx和2hy.设ê=[-1，1]×[-1，1]是ξ-η平面上的参考单元，其四个顶点分别为和四条边为和则存在可逆放射变换

(2.1)

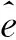
(2.2)

(2.3)

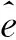
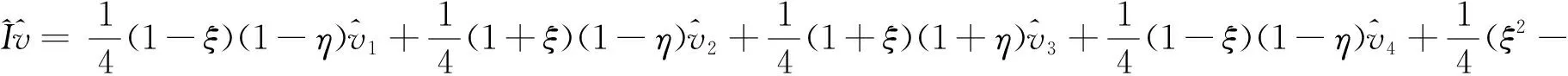
(2.4)

3 收敛性分析

取上面假设中的V=L2(Ω),W=L2(Ω)×L2(Ω),D=0×L2(Ω)⊂H′×M′,则(H1)-(H3)都成立；若h为Ω⊂R2的拟一致矩形剖分，he为单元e的直径，h=max{he;e∈h},则(H4)也成立，这时s(h)=ch-1, 即:

‖φh‖1≤ch-1‖φh‖0, ∀φh∈Hh∩(H1(Ω))2.

要讨论(H5)成立，为此我们引入下面的引理.

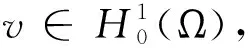
(divφ,v)=-(φ,v)

(3.1)

定理1 如果存在算子rh∶H→Hh使得对于φ∈H都有:

b(φ-rhφ,vh)=0, ∀vh∈Mh

(3.2)

则问题(1.3)存在唯一的解(ψh,uh)∈Hh×Mh并有下列误差估计:

‖ψ-ψh‖0≤‖ψ-rhψ‖0+|u-uh|1,

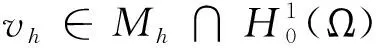
(3.3)

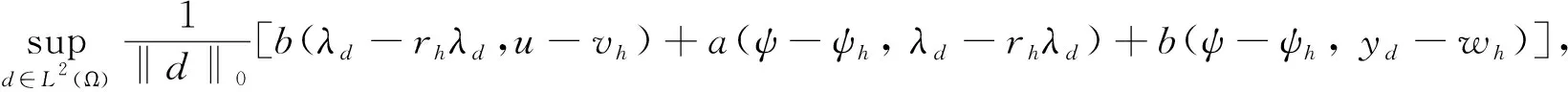
∀vh,wh∈Hh

(3.4)

(3.5)

并且有先验估计:

‖λd‖1+‖yd‖2≤D‖d‖0

(3.6)

下面来构造有限元空间Hh和Mh以及算子rh满足定理1的条件.

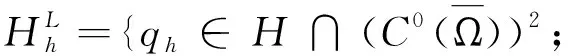
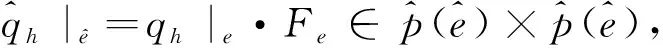
(3.7)

同时定义泡函数be(x,y)为:

(3.8)

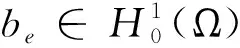
B=(span{be;e∈h})2

(3.9)

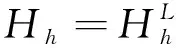
(3.10)

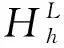
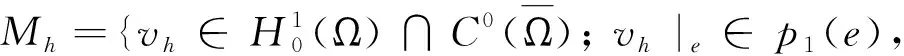
(3.11)

在这里我们需要定义v的插值函数Iv∈Mh,

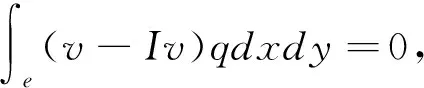
(3.12)

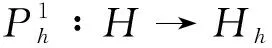
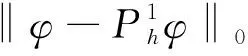
(3.13)

定义rh∶H→Hh使得, ∀φ∈H,

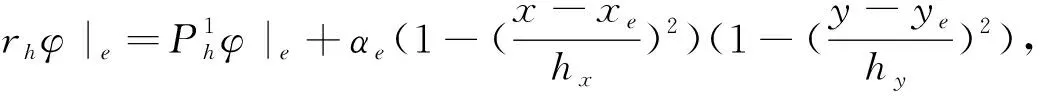
(3.14)

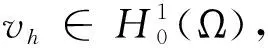
b(φ-rhφ,vh)=(div(φ-rhφ),vh)=-(φ-rhφ,vhdxdy.

由Mh的定义知，vh|e是常向量，所以定理1的(3.2)式成立，只需:

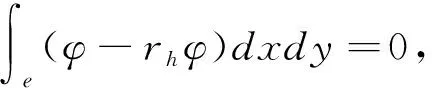
(3.15)

由rh的定义得:

(3.16)

这样当αe满足(3.15)时，rh满足(3.2)式.由前面的单元构造知道|e|=4hxhy又经过计算得到:

(3.17)

(3.18)

故由(3.16)和Hölder不等式得:

|αe|=

(3.19)

由rh的定义及(3.17)，(3.18)得到:

‖φ-rhφ‖0,e=

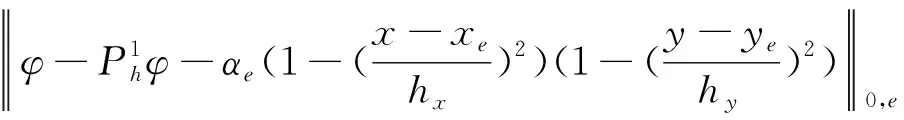
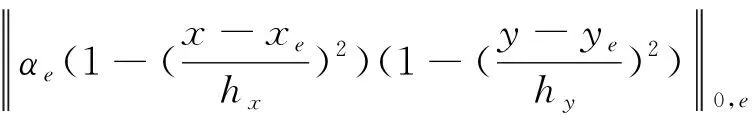
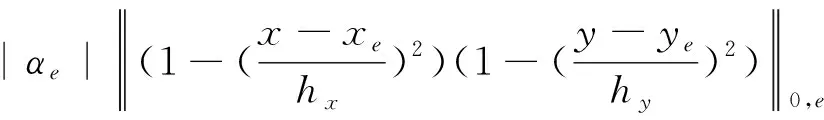
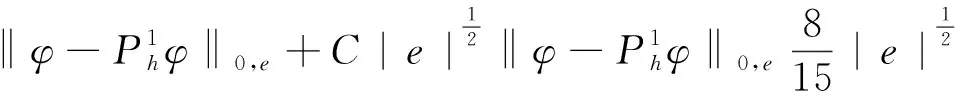
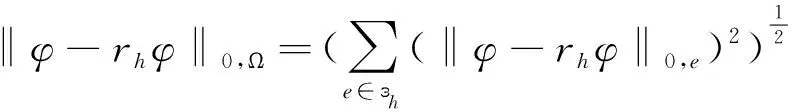
(3.20)

因此,Hh,Mh和rh满足定理1，于是得到下面的结论.

h‖ψ-ψh‖0+‖u-uh‖0≤Ch2‖f‖0

(3.21)

证明设ρh∶H2(Ω)→Mh为L2投影算子, 则:

|u-ρhu|1≤Ch|u|2, ∀u∈H2(Ω)

(3.22)

由(3.3)、(3.18)、(3.20)得到：

‖ψ-ψh‖0≤C(‖ψ-rhψ‖0+|u-ρhu|1)≤Ch‖f‖0

(3.23)

下面我们来估计‖u-uh‖0，由引理1，Hölder不等式及(3.6)、(3.18)、(3.22)得到:

b(λd-rhλd,u-ρhu)=(div(λd-rhλd),u-ρhu)=-(λd-rhλd,(u-ρhu))≤

C‖λd-rhλd‖0|u-ρhu|1≤Ch2‖u‖2‖λd‖1≤Ch2‖u‖2‖d‖0

(3.24)

α(ψ-ψh,λd-rhλd)≤C‖ψ-ψh‖0‖λd-rhλd‖0≤Ch‖ψ‖1h‖λd‖1≤Ch2‖u‖2‖d‖0

(3.25)

b(ψ-ψh,yd-ρhyd)=(div(ψ-ψh),yd-ρhyd)=-(ψ-ψh,(yd-ρhyd))≤

C‖ψ-ψh‖0‖yd-ρhyd‖1≤Ch‖ψ‖1h‖yd‖2≤Ch2‖u‖2‖d‖0

(3.26)

将(3.24)、(3.25)、(3.26)代入(3.4)得到:

‖u-uh‖0≤Ch2‖u‖2≤Ch2‖f‖0

(3.27)

由(3.23)、(3.27)即可证明本定理.

参考文献:

[1] 罗振东.混合有限元法基础及其应用[M].北京:科学出版社，2006.

[2] BREZZI F, FORTIN M.Mixed and hybrid finite element methods[M].Springer-Verlag,1991.

[3] RAVIART PA,THOMAS P A. A mixed finite element method for 2nd order elliptic problems[J]. Lecture notes in math:springer-verlag,1977(68):292-315.

[4] DOUGLAS JR J, ROBERTS J E.Global estimates for mixed methods for second order elliptic equations[J]. Math.Comp,1985,169(44):39-52.

[5] 黄建国.一个混和元的最大模估计及超收敛估计[J].计算数学,1991,13(3):174-279.

[6] 庞之垣.混合有限元法的误差估计[J].计算数学,1986,8(4):337-344.

[7] 石东洋，梁慧.一个新的非常规型各向异性矩形元的超收敛分析及外推[J].计算数学,2005,27(4):369-382.

[8] CIARIT P G. The finite method for elliptic problem[M]. Amsterdam: North-Holland Publ., 1978.

[9] 林群,严宁宁.高效有限元构造与分析[M].石家庄:河北大学出版社,1996.

[10]王烈衡,许学军.有限元方法的数学基础[M].北京:科学出版社,2004.