大脑皮层信号作用下人体步态节律运动的探讨
董 玮 王如彬 张志康
(华东理工大学信息科学与工程学院认知神经动力学研究所,华东理工大学理学院数学系,上海 200237)
引言
早在1911年,Graham Brown实验证明了步态的基本模式是由脊髓系统产生的,并不需要大脑皮层的运动指令[1-2],这里的脊髓系统就是中枢模式发生器(central pattern generator,CPG)。当时的解剖学对于CPG的了解还很少,因此Graham Brown的这一观点并不被广大研究者所认可。直到1961年,Wilson通过解剖蝗虫的实验明确了生物体内(无脊椎动物)CPG的存在。从那时起,脊椎动物的CPG证据也逐渐显现,研究者们开始对许多低等动物的CPG进行了模拟仿真。
高等动物及人类的节律运动,同样是由CPG所产生和控制的。现代的研究,不仅证实了控制人体运动CPG的存在,同时证明了它的稳定性和适应性[3-4],人体控制运动的CPG不仅能够产生节律模式,而且对各种环境具有很好的适应性。近几年,有许多研究者对CPG模型展开了研究,修正了生物CPG的数学方程式,使其相对简单化。这些数学化的CPG模型广泛应用于工程应用等方面,例如:机器人控制,动物或人类运动的建模和仿真,脊髓受损病人的康复控制[5]。一些研究者也对于 CPG的一些重要特性进行针对性的研究,例如强直性输入和感应反馈、稳定性振荡和偶联关系等。通过仿真研究,可以理解CPG的复杂性,为CPG在工程方面的应用提供坚实的基础。
现有的CPG模型都是以自发节律行为作为研究对象的,模型本身没有体现大脑皮层的指令性调节作用,为了更好的体现大脑皮层信号对于CPG神经网络具有的调控性,本研究对原有模型各参数间的相互联系进行了重新构建,重点强化了输入刺激信号与CPG内部各连接参数的关系,突出表达了输入信号对于CPG内部的调控,从理论上实现了自发节律与大脑调节性节律运动的共存,做到大脑信号与CPG模型的统一,使其得出与实际情况更为接近的仿真结果。
1 生物CPG模型
生物CPG分为链式和网状两种结构[6]。其中链式结构多见于低等生物。网状CPG存在于脊椎动物体内,控制动物体各肢体间的协调运动[7-8]。对于高等动物和人类而言,其体内的 CPG更为复杂,是链式结构和网状结构的相互结合[9-10]。
目前,有3种神经振荡器模型被广泛应用于生物CPG的模拟研究。第一种是Matsuoka神经振荡器[11],着重体现的是CPG的周期循环性;第二种是七思鳗振荡器[12],着重体现的是 CPG的相位耦合性质;第三种是 Van der Pol神经振荡器[13-17],体现的是CPG产生节律运动时,生物体相应部位关节角度的相对关系。其中,Matsuoka神经振荡器是应用最为广泛的,关于Matsuoka神经振荡器和生物CPG之间的相互关系可参阅文献[18]。
现阶段,对于节律性运动的理论研究,都是以CPG模型为基础,进行的理论性预测。不同的生物体具有不同的CPG结构,某一生物体内部的不同部位的CPG结构亦是有所差别的。对于人体的腿部节律性步态运动的研究,即需要在建立腿部CPG模型时结合腿部的肌肉骨骼结构。本研究中的CPG网络模型就是以Matsuoka神经振荡器为理论基础,并结合了Hill腿部肌肉简化模型的结构来组建的,其中包含了3组二维神经振荡器单元,分别表示腿部的3个关节—臀(hip)、膝(knee)、踝(ankle)。每个神经振荡器单元内含有2个神经元集群,分别表示对应关节部位的两种肌肉集群—伸肌(extensor)和屈肌(flexor),模型示意图参见图1,具体的模型介绍可参见文献[19],该 CPG模型中,输出量 Yi是一个状态评定量,表示肌肉的状态形式,范围在0~1之间,1表示完全活跃状态,0表示不活跃状态。
2 对原有模型的修正
2.1 步态模式的不同表现形式
生物学研究表明,CPG网络可以与外部输入信号耦合,传递输入模式,因此改变输入激励信号可以调节网络的输出行为,实现步态的转换[20]。目前的CPG模型的腿部模式的模拟研究,仅仅局限于单一模式下的运动状态,无法将各种不同运动模式进行转换,也就无法体现大脑皮层信号对于节律性运动的指令性调节作用。已有的文献中也曾介绍了关于不同模式的节律性运动输出:由Zhang等人的CPG建模仿真及其实验,阐述了腿部运动的两种基本形态,即步行状态[8](见图 2)和踏车运动状态[6](见图3)。
上述存在的实验结论,都是互抑制神经网络构成的人体腿部CPG网络模型,通过不同的参数设置,对不同的步态表现形式做出了一定的仿真实现,具体的内容可参看文献[6,8]。然而,这两种步态形式的体现仅表现为单一形式的出现,两种模式之间并没有表现出一定的关联性。因此,试图表现不同形式步态运动间的相互关联性,表达出步态模式之间是可以相互转换的。以此为依据,来对模型进行修正。

图1 CPG模型的构建原理。(a)腿部肌肉骨骼结构[8];(b)二维神经振子模型[2];(c)基于腿部模型的 CPG框架;(d)CPG的网络模型[6]Fig.1 The theoretic foundation of CPG model.(a)muscle-skeleton structure of leg[8];(b)neural oscillator theory[2];(c)CPG frame based on leg model;(d)CPG network model[6]
2.2 体现不同步态运动之间相互转换关系的模型
在实际生活中,人体的步态运动多种多样,比如,行走、奔跑、踏步等,这些多种多样的步态运动形式是如何通过现有的CPG网络模型来体现的呢?由上述的例子我们可以知道,通过对CPG网络内部各连接参数的改变,可以得到不同的运动形式,这些运动形式可以从模式及频率上产生不同的变化,然而,由于理论与实际的复杂关系,目前的研究,并不能准确的将某种节律运动与特定的CPG模式进行一一对应的解释,这里,仅仅是为了说明CPG输出具有不同的表现模式,且各模式间具有一定的转换关系,即关联性的体现,这种模式变化的表现形式是符合生物实际运动现象的,做到了步态模式间的相互转换,正是理论与实际的进一步接近。CPG神经网络是表现腿部节律运动的主要网络结构,这一神经网络的运作并不直接受大脑控制,而是一种自行运作的模式。原有的CPG模型一直是以强制性输入作为刺激信号的,仅体现了自发情况下的运动状态。然而,实际生活中不同的运动形式是由大脑进行调节的,当大脑一旦确定了某种运动模式后,CPG的自发运动模式使得特定的运动形式能够有节律的进行下去,我们试图体现不同模式的转换,也就是在自发性运动的CPG网络中考虑了大脑皮层的调节作用,就目前的仿真研究而言,多以正弦信号作为大脑皮层的指令信号作为研究对象[20]。修正后的CPG理论模型的数学表达式为

式中,Kf和Kt分别是节律性感应增益和强直性输入增益(模型中 Kf=1,Kt=1),i,j表示神经元 1 ~12,Xi表示第i个关节的神经元集群的两种状态—屈肌(flexor)与伸肌(extensor),νi表示肌肉恢复过程的适应性,ωi,j表示双腿共12个神经元集群之间的相互联接权重,τ是状态常数,T是适应度常数,输出Yi是一个状态评定值,1表示完全活跃状态,0表示不活跃状态,详细的参数介绍可参见文献[19]。
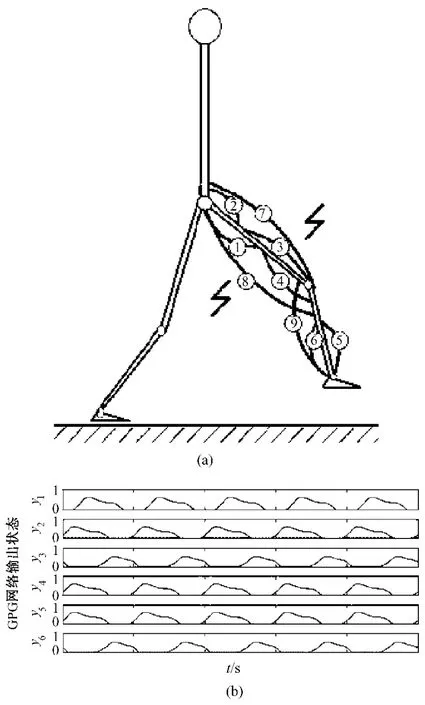
图2 步行运动情形。(a)步行运动时的肌肉模型;(b)仿真结果的CPG输出模式。Fig.2 Walking state.(a)muscle skeleton structure model when walking;(b)the output of CPG model in simulation
式(1)中,由*号标示出的式子是对原有CPG模型中各参数之间的修正,加强了彼此的联系,使其更好的表达出了输入信号与CPG网络间的调节关系,修改后的模型,其结果更加符合生物实际中的现象。原有模型的输入信号 r与CPG模型内部各参数之间没有关联性,即仅依赖于常数信号来模拟自发节律运动现象,修改后的输入信号与CPG网络内部的参数联系紧密,用正弦模拟脑部指令信号,从而实现步态的模式及频率的转变,以从模型上更好的反映出步态的变化性特点,实现了更接近于实际的模型构建。
3 仿真结果

图3 踏车运动情形。(a)周期性踏车运动时的肌肉模型;(b)仿真结果的CPG输出模式Fig.3 Cycling state.(a)muscle skeleton structure model when cycling;(b)the output of CPG model in simulation
在节律性运动情况下,以脊髓为中心的运动控制是以低位神经系统并通过自激振荡的网络而自发地产生神经信号。这类神经信号可以设定为内刺激,实际上内刺激可看作CPG模型的常值输入信号。而当步态运动的节律改变时,大脑会给肢体发出运动节律改变的指令。而大脑皮层对肢体运动的输入信号大多取为正弦波的形式[20]。因此,在仿真中,用常数信号表示CPG的自激振荡刺激,用正弦波信号来表示大脑的指令刺激,当大脑产生瞬间的指令信号时,CPG的输出模式就会发生一定的转换,从而实现了大脑的调节功能。
3.1 模式间的相互转换
这里,仅列举两种不同的CPG输出模式间的相互转换,根据正弦波的3种不同状态,即表示了大脑的3种不同的调节指令,可以得到3种CPG输出模式的转换关系:
状态1:当正弦信号即大脑指令信号的作用为正半周期时,CPG模型的输出模式可由模式1转变为模式2(见图4);
状态2:当正弦信号即大脑指令信号的作用为负半周期时,CPG模型的输出模式可由模式2转变为模式1(见图4);
状态3:当正弦信号即大脑指令信号的作用为完整周期时,CPG模型的输出模式是不会发生变化的。
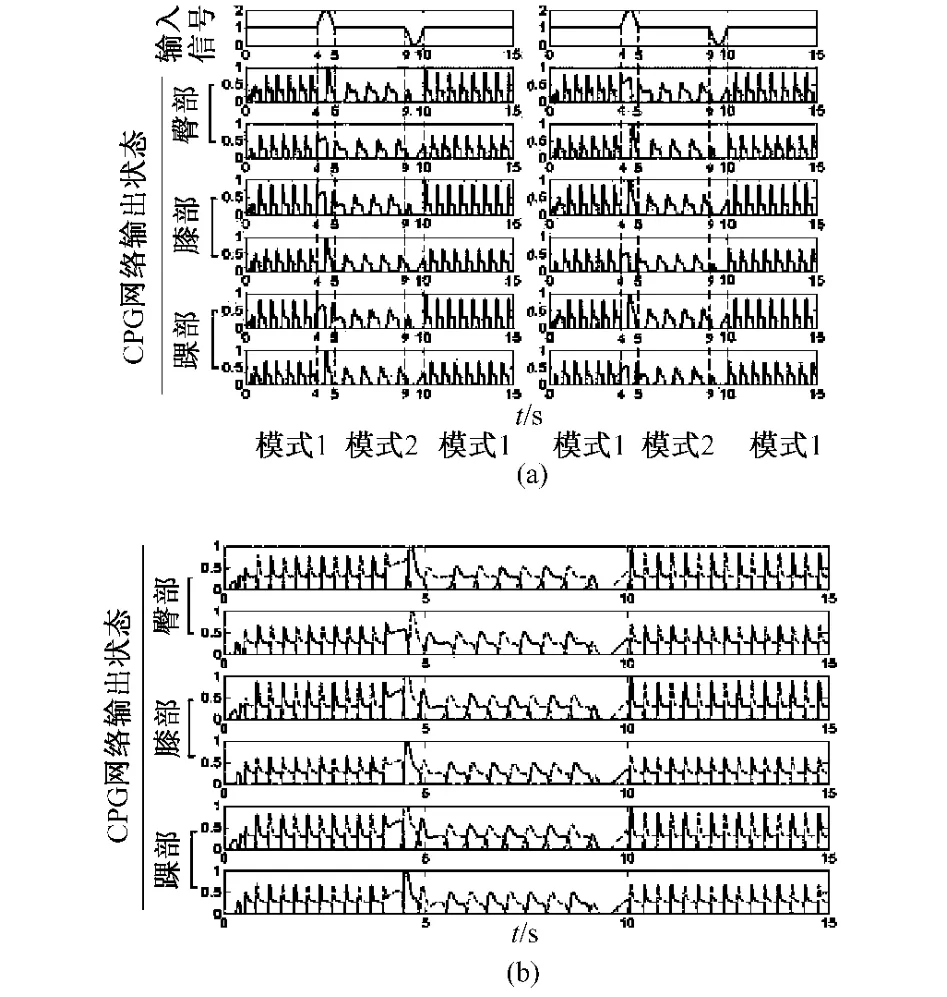
图4 模式转换。(a)腿部运动的节律性;(b)腿部运动相位互补的协调性Fig.4 Interchange between modes.(a)the rhythm characteristic of the leg movement;(b)the coordinated characteristic of the leg movement,the locked outof-phase
3.2 同种模式下不同频率状态的相互转换
大脑调节信号rbrain除了可以引起CPG不同模式之间的相互转换,对于同一种模式的不同频率下的状态同样可以实现转换。由于,大脑调节信号rbrain的正弦周期Tr与CPG网络的时间参数 τ和 T有着紧密联系,适当调节影响参数b、c的值,仿真实验也可以得到同种输出模式下不同频率之间的相互转换,对应的,也存在3种状态:
状态1:当正弦信号即大脑指令信号的作用为正半周期时,CPG模型的输出频率可由快状态转变为慢状态(见图5);
状态2:当正弦信号即大脑指令信号的作用为负半周期时,CPG模型的输出频率可由慢状态转变为快状态(见图5);
状态3:当正弦信号即大脑指令信号的作用为完整周期时,CPG模型的输出频率将不发生改变。
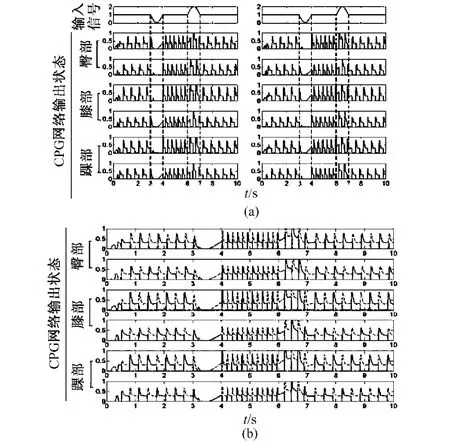
图5 同种模式下的频率转换。(a)腿部运动的节律性;(b)腿部运动相位互补的协调性Fig.5 Interchange between frequencies in the same mode.(a)therhythm characteristicofthe leg movement;(b)the coordinated characteristic of the leg movement,the locked out-of-phase
所修正的模型,体现出了两种不同的转换形式:模式转换和频率转换,模型各参数的设定具有以下特点:
1)在大脑指令信号rbrain不变的前提下,参数b,c的取值直接影响转换的类别,当b逐渐增大时,转换类型由频率转换变为模式转换,例如:频率转换时,b=0.01(见图5);模式转换时,b=0.1(见图4)。而b又不能无限增加,当b达到一定的数值时,就会破坏输出模式的节律性。参数c则是影响着转换前后输出的频率变化程度,c越大变化越明显。
2)参数τ主要控制模式的类别,τ越小,输出结果接近于模式1(形状较尖锐);τ越大,输出结果接近于模式2(形状较缓和)。
3)参数T则控制着运动输出的初始频率,T越大输出模式的初始频率亦越快。
4 讨论和结论
CPG是一种低级神经中枢系统,控制着生物体的节律性运动,其运动过程并不直接受大脑的信号作用,但对于人类而言,大脑的调节指令是不容忽视的,大脑对于节律运动的调节功能必然存在。原有的CPG建模仅仅表现了 CPG的自激行为,本研究通过对原有CPG模型内部各参数间的连接关系的函数构建,使得各参数与输入信号的联系更加密切,随着输入信号的变化CPG网络内部参数亦发生改变,从而实现模式和频率上的转换与恢复,理论上体现了大脑皮层信号对于CPG网络的影响,很好的反映出步态节律运动过程中,大脑信号对其步态的模式和频率起到调节作用,既可以改变运动的频率又可以改变运动的模式,这一修正,更加完善了CPG模型本身的理论性意义,将其理论性的仿真研究更加接近于生物学的实际现象,更符合生物学的实际情形,这也将更有利于CPG理论在实际工程中的应用,更有利于拓宽其理论研究及实际应用的道路。
但由于目前生物实验方面研究的局限性,仅仅将运动形式划分为模式和频率上的变换。建立理论模型与实际生物现象之间更密切的对应关系将是今后研究的重点内容。
[1]Brown G.The intrinsic factors in the act of progression in the mammal[J].Proceedings of the Royal Society B:Biological Sciences,1911,84:308-319.
[2]Grillner S.Some aspects on the descending control of the spinal circuits generating locomotor movements[A].In:Herman RM,et al,eds.Proceedings of an International Conference on Neural Control of Locomotion,Advances in behavioral biology[C].New York:Plenum,1976.77-82
[3]Kiehn O,ButtSJ. Physiological,anatomicaland genetic identification of CPG neurons in the developing mammalian spinal cord[J].Prog Neurobiol,2003,70:347 - 361.
[4]Choi JT,Bastian AJ.Adaptation reveals independent control networks for human walking[J].Nature Neuroscience,2007,10:1055-1062
[5]Gerasimenko YP,Makarovskii AN,Nikitin OA.Control of locomotor activity in humans and animals in the absence of supraspinal influences[J].Neurosci Behav Physiol,2002,32:417-423.
[6]Zhang Dingguo,Zhu Kuanyi,Zheng Hang.Model the leg cycling movement with neural oscillator[A].In Piscataway NJ,ETATS-UNIS,eds.IEEE International Conference on Systems,Man and Cybern[C].Netherlands:IEEE,2004.1:740-744
[7]Warrick H,Cohen AH.Serotonin modulates the central pattern generator for locomotion in the isolated lamprey spinal cord[J].Biol,1985,116:27 -46.
[8]Zhang Dingguo,Zhu Kuanyi.Modeling biological motor control for human locomotion with function electrical stimulation[J].Biol Cybern,2007,96:79-97
[9]Marder E,Bucher D.Central pattern generators and the control of rhythmic movements[J].Current Biology,2001,11(23):986-996.
[10]Zehr EP,Fujita K,Stein RB.Regulation of arm and leg movement during human locomotion[J].The Neuroscientist,2004,10(4):347-361.
[11]Matsuoka K.Mechanisms of frequency and pattern control in the neural rhythm generators[J].Biol Cybern,1987,56:345-353.
[12]Ijspeert,Auke J,Kodjabachian J.Evolution and development of a central pattern generator for the swimming of a lamprey[J].Artificial Life,1999,3(5):247-269.
[13]Dutra MS,Armando C,Filho P,et al.Modeling of a bipedal locomotor using coupled nonlinear oscillators of Van der Pol[J].Biol Cybern,2003,88:286-292.
[14]张健鹏,王如彬,沈恩华,等.关于昆虫步态运动时神经控制机理的动力学分析[J].动力学与控制学报,2009,7(1):29-34.
[15]张健鹏,王如彬.基于被动力学的昆虫运动动力学建模与分析[J].力学季刊,2009,30(1):39-43.
[16]Zhang Zhikang,Wang Rubin,Yasuda K.On joint stationary probability dendity function of nonlinear dynamic systems[J].Acta Mechanica,1998,130:29 -39.
[17]Wang Rubin,Kusumoto S.A new equivalent non-linearization technique[J].Probabilistic Engineering Mechanics,1996,11:129-137
[18]Zhang Dingguo,Zhu Kuanyi.Compiter simulation study on central pattern generator:from biology to engineering[J].International Journal of Neural System,2006,16(6):405-422.
[19]董玮,王如彬,沈恩华,等.节律性步态运动中 CPG对肌肉的控制模式的仿真研究[J].动力学与控制学报,2008,6(4):327-331.
[20]Todorov E.Cosine tuning minimizes motor errors[J].Neural Computation,2002,14:1233 -1260.

