慎对课堂的意外 拾拣智慧的珠玑
——记一道课本例题的意外收获
●
(嘉兴市第一中学 浙江嘉兴 314050)
0 前言
在平常的教学过程中,总会遇到这种情况:当教学活动正按事先预设的方向前进时,突然有学生提出与教学设计完全不同,但又非常“闪光”的想法,若对这“意外”发言给予重视、肯定,合理施教,可能会打乱整个教学设计,但也可能会得到意外的收获.笔者在讲解课本例题时就曾遇到过这种情况,现整理成文以供大家参考.
1 课堂回顾
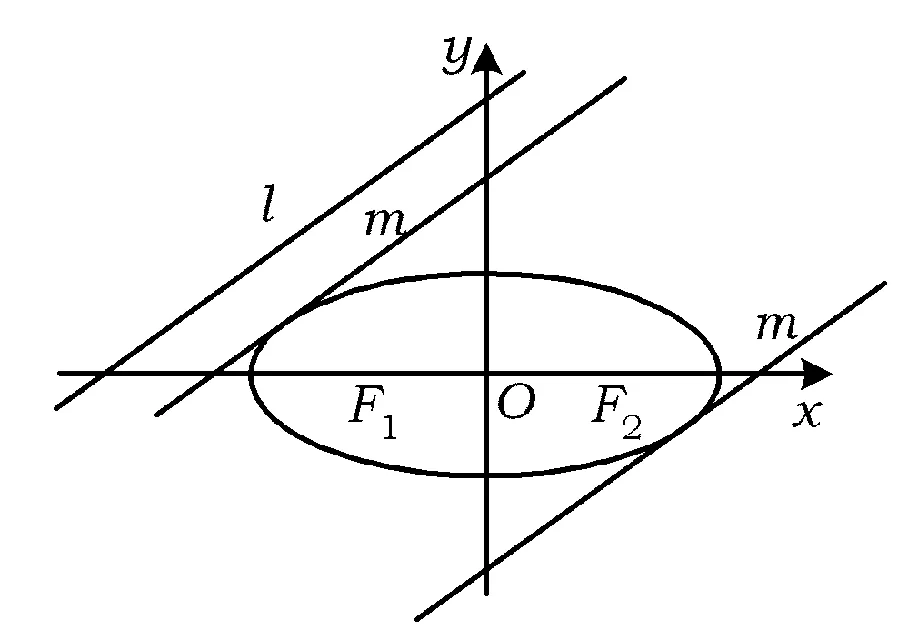
图1
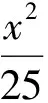
笔者在讲解此题时是用数形结合的方法求解的.作出直线l及椭圆,观察图形可以发现利用平行于直线l且与椭圆只有一个交点的直线,可以求得相应的最小距离.让学生感受到数形结合在解圆锥曲线中的重要应用,也让学生深刻体会了如何去求与已知直线平行且与椭圆只有一个交点(切线)的直线方程.刚讲解完此题,有位学生突然举手且发言:“老师,此题不需要画出图像,根据所给方程,可以很快求出答案”.笔者心里一惊,请他发言.
生:解决本题的关键是求出椭圆的切线.令切线方程为4x-5y+c=0,则

于是

确实和答案完全一样.其他同学也很惊讶.
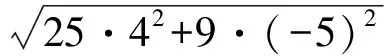
生:其实c就等于直线常数项的平方,等于直线方程中x系数的平方乘以椭圆长半轴的平方再加上直线方程中y系数的平方乘以椭圆短半轴的平方.
其他同学听得一头雾水.
师:你是怎么知道的?
生:就是您刚才讲解例题时,我发现的.
师:这个方法是只对于这个题目成立,还是对于一般的直线方程和椭圆也成立呢?我们一起来探究.
2 探究

(并请该生上黑板板演.)
证明联立方程
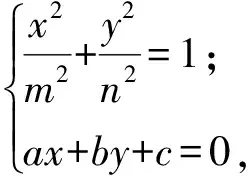
消去y得
(b2n2+m2a2)x2+2acm2x+m2c2-b2m2n2=0,
于是
Δ=(2acm2)2-4(b2n2+m2a2)(m2c2-
b2m2n2)=
4m2b2n2(m2a2+n2b2-c2).
令Δ=0,得
c2=m2a2+n2b2,
从而

不但答案是肯定的,而且又有学生发现:当c2
师:也许是巧合,让我们得到了一个判断直线与椭圆位置关系的简便方法.

(1)若c2=m2a2+n2b2,则直线l与椭圆有且只有1个交点(相切);
(2)若c2 (3)若c2>m2a2+n2b2,则直线l与椭圆没有交点(相离). 直线与二次曲线位置关系的判别,常用的方法是判别式,而利用“Δ”法计算量往往很大.上述几个性质是从“Δ”法中提炼出一般的结论:利用直线的参数与二次曲线参数之间的关系,可以快速地判断直线与二次曲线的位置关系.直观性强、简单易记,应用起来十分方便,请看以下的例子. 解因为 62·9-52·16=-166<32, 所以由性质2可知直线l与双曲线相交. 例3直线y=mx+1与椭圆x2+4y2=1有且只有1个交点,则m2=________. 解由性质1可得 解得 分析结合图形发现,求出与直线l平行且与椭圆相切的直线,由此可以求得相应的最小距离. c2=22·2+(-1)2·1=9, 得 c=-3(c=3舍去), 于是最小距离为 例5试就实数k的取值情况,讨论方程x2+4(kx+k+2)2-12=0的实根个数. 分析此题若用判别式来求解,运算较为复杂,但用上述性质来处理却十分容易. 解令y=kx+k+2,则方程变为 x2+4y2-12=0, (k+2)2=12k2+3, 即 11k2-4k-1=0, 解得 例6设m∈R,在平面直角坐标系中,已知向量a=(mx,y+1),向量b=(x,y-1),a⊥b,动点M(x,y)的轨迹为E. (1)求轨迹E的方程,并说明该方程所表示曲线的形状. (2009年山东省数学高考文科试题) 解(1)略. x2+4(kx+t)2=4, 即 (1+4k2)x2+8ktx+4t2-4=0. 要使切线与轨迹E恒有2个交点A,B,由推论1可得 t2<4k2+1, 且 于是 y1y2=(kx1+t)(kx2+t)= k2x1x2+kt(x1+x2)+t2= 于是 5t2-4k2-4=0, 即 5t2=4k2+4且t2<4k2+1, 从而4k2+4<20k2+5恒成立.又因为直线y=kx+t为圆心在原点的圆的一条切线,由推论2可得 t2=(k2+1)r2, 于是 又l与轨迹E只有一个公共点B1,由推论1可得 由式(1),式(2)得 此时,点A,B重合为点B1(x1,y1).由 得 x1=x2, 从而 因为点B1(x1,y1)在椭圆上,所以 得 在Rt△OA1B1中, |A1B1|2≤5-4=1, 课后,笔者还给学生布置了思考题:能否把我们的结论推广到其他的圆锥曲线呢?从学生反馈的作业中归纳了以下6个推广. (1)若m2=a2k2+b2,则直线l与椭圆有且只有1个交点(相切); (2)若m2 (3)若m2>a2k2+b2,则直线l与椭圆没有交点(相离). 推广2已知圆方程x2+y2=r2,直线l:ax+by+c=0. (1)若c2=(a2+b2)r2,则直线l与圆有且只有1个交点(相切); (2)若c2=(a2+b2)r2,则直线l与圆有2个交点(相交); (3)若c2=(a2+b2)r2,则直线l与圆没有交点(相离). (1)若c2=m2a2-n2b2,则直线与双曲线有且只有1个交点(相切); (2)若c2>m2a2-n2b2,则直线与双曲线有2个交点(相交); (3)若c2 (1)若c2=n2b2-m2a2,则直线l与双曲线有且只有1个交点(相切); (2)若c2>n2b2-m2a2,则直线l与双曲线有2个交点(相交); (3)若c2 推广5已知抛物线y2=2px,直线l:ax+by+c=0. 推广6已知抛物线x2=2py,直线l:ax+by+c=0. 本文记录的是笔者教学活动中的一次“意外”.在平常的教学过程中,常常会遇到突如其来的“意外”.若能结合教学内容进行研究,既能自然地得到学生容易接受的结果,又能使学生通过自己的探索,沟通知识之间的内在联系.这节课的“意外”通过教师的点评、归纳,学生不但全面掌握了直线与圆锥曲线有且只有1个公共点的求法,而且掌握了根据方程快速判定直线与圆锥曲线位置关系的方法,提升了解题能力. 由此看来,在平时教学中,教师若能放手让学生去思考、探索,充分发挥学生的主观能动性,注意学生的“闪光点”,并通过问题探究引导学生在收集、整理、归纳中获得新知识,在知识的联系中进行有效整合,这不仅对学生能力的培养和提高很有益处,而且也使课堂充满生机,收获不断.3 应用
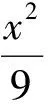
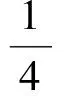
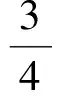
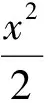
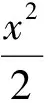







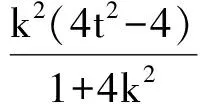

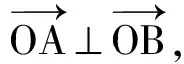
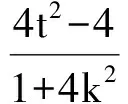

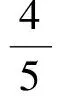





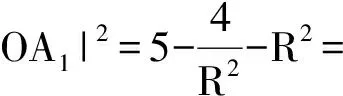
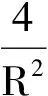
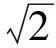
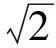
4 推广
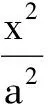
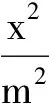




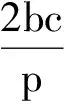
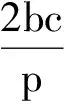
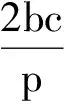
5 反思

