集值映射空间上的κ-Fréchet Urysohn性质

郭先一,李祖泉

(杭州师范大学 理学院,浙江 杭州 310036)

κ-Fréchet Urysohn空间是弱于Fréchet空间从而弱于第一可数空间的一类拓扑空间,它最初是由Arhangel’skii A V作为κ-伪特征的自然推广引入的.Liu C, Ludwig L D[1]对κ-Fréchet Urysohn空间进行过系统的研究.在单值连续映射空间Ck(X)中κ-Fréchet Urysohn性质的刻画是由Sakai M[2]得到的,Ck(X)是Frechet空间,严格Fréchet空间和强Fréchet空间的等价证明在[3]中能看到.虽然Ck(X)是Ck(X)的闭子空间,但是κ-Fréchet Urysohn空间对子空间甚至是闭子空间没有遗传性.所以Ck(X)空间的κ-Fréchet Urysohn性质的研究是有意义的.本文给出了点紧连续集值映射空间Ck(X)的κ-Fréchet Urysohn性质与基本空间X的对偶定理,获得了Ck(X)是κ-Fréchet Urysohn空间的等价性证明.

1 预备知识

该文中,拓扑空间X是Tychonoff的,K(X)表示X的所有非空紧子集族,ω表示可数序数,ω1表示第一个不可数序数,R表示实直线,C(X)为X到R上的所有单值连续映射族,M(X,Y)为X到Y上的所有集值映射族,Ck(X)为X到R上的所有点紧致的连续集值映射族,并且赋予紧开拓扑.文中未定义的术语和符号均以[3-5]为准.

设f∈Ck(X),对A⊂X,记f(A)=∪x∈Af(x);对B⊂R,记

f+(B)={x∈X:f(x)⊂B};
f-(B)={x∈X:f(x)∩B≠∅}.

对于X的子集K,R的子集U,V,记

W+[K;U]={f∈Ck(X):f(K)⊂U};
W-[K;V]={f∈Ck(X):f(x)∩V≠∅,x∈K}.

定义1[6]以所有形如W+[K,U],W-[K,V]的集为子基作为Ck(X)的拓扑,该拓扑称为Ck(X)上的紧开拓扑,其中K∈K(X),U,V为R的开子集.

以下谈到的Ck(X)上的拓扑均指紧开拓扑.

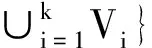
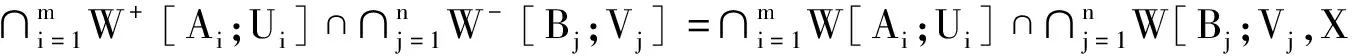
定义2对于任意A,B⊂R,定义ρ(x,A)=inf{|x-y|:y∈A},ρ(A,B)=sup{ρ(x,B):x∈A}和d(A,B)=sup{ρ(A,B),ρ(B,A)},对于x∈R,记d(x,A)=d({x},A).

引理2设X是拓扑空间,Ck(X)为X到R上的所有点紧致的连续集值映射族,则Ck(X)的紧致处一致收敛拓扑等价于紧开拓扑.

证明只须将[7]中定理1的空间Y换成R.

2 主要结果

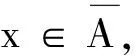
显然,第一可数空间⟹Fréchet空间⟹κ-Fréchet Urysohn空间.

定义5空间X的子集族{Aα:α∈Λ}称为点有限的,若对于x∈X,{α:x∈Aα}是有限的.

定义6空间X的子集族{Aα:α∈Λ}称为强点有限的,若对于α∈Λ,存在开集Uα⊂X使得Aα⊂Uα且{Uα:α∈Λ}是点有限的.

定义7空间X的非空子集族F称为是moving off的,若对于任意K∈K(X),存在F∈F使得K∩F=∅.

定义8空间X的子集族F称为是强moving off的,若对于任意F∈F,存在开集UF使得F⊂UF且{UF:F∈F}是moving off的.

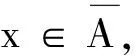
定理1对于空间X,下列结论是等价的:

1)Ck(X)是开可数tightness空间;

2)X的每一个moving off紧子集族都存在一个可数强moving off子族.

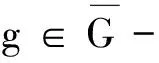
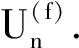
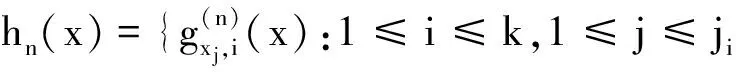
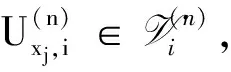
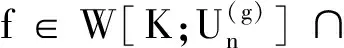
定义10空间X的子集族{Aα:α∈λ}称为紧有限的,若对于任意K∈K(X),{α:K∩Aα≠∅}是有限的.{Aα:α∈λ}称为强紧有限的,若对于任意K∈K(X),存在开集Uα使得Kα⊂Uα,并且{α:K∩Uα≠∅}是有限的.

对于空间X,A⊂X,记s0(A)=A.对于α∈ω1,令sα(A)为∪β<αsβ(A)中的序列极限点集.s(A)=∪α∈ω1sα(A)称为A的列型闭包.

定理2对于空间X,下列结论是等价的:

1)Ck(X)是κ-Fréchet Urysohn空间;

2)Ck(X)的任意开集的列型闭包是闭集;

3)X的每一个moving off紧子集族都存在一个可数子族是强紧有限的;

4)对于X的每一个moving off紧子集族列{Kn}n∈ω,存在Kn∈Kn使得{Kn}n∈ω是强紧有限的.

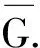
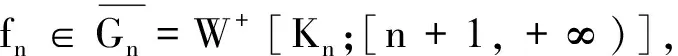
4)⟹1).证明方法与定理1中的2)⟹1)完全相似.

[1] Liu C, Ludwig L D.κ-Frechet Urysohn spaces[J]. Houston J Math,2005,31:391-401.

[2] Sakai M.κ-Fréchet Urysohn property ofCk(X)[J]. Topology Appl,2007,154:1516-1520.

[3] 林寿.度量空间与函数空间的拓扑[M].北京:科学出版社,2004:213-219.

[4] 郭先一,李祖泉.集值映射空间上可数强fan tightness[J].杭州师范大学学报:自然科学版,2010,9(1):23-25.

[5] Engelking. General topology[M]. Warszwa: Polish Scientific Publishers,1977:78-91.

[6] Li Zuquan. Tightness and fan tightness on multifunction spaces[J]. J Math Res Exposition,2008,28(4):1007-1012.

[7] 李祖泉.集值映射空间的度量化[J].工程数学学报,2008,25(3):567-570.

[8] 李祖泉.集值映射空间在紧开拓扑下的0性质[J].数学研究与评论,2007,27(4):933-938.