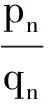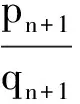以整数幂为元素的连分数对数的线形型下界
庄晨婕
(杭州师范大学 理学院,浙江 杭州 310036)
1 引言与预备知识
自A.Baker[1-3]对代数数的对数的线性形式的下界做出开创性成果以来,关于对数线性型下界估计的研究一直是超越数论研究中的中心课题,并不断出现新的有成效的方法和成果[4-5].1991年,朱尧晨[6]给出了一类超越连分数代数无关性的结果.于秀源等[7-8]给出了一类连分数的超越性,以及以anx(an为正整数)为元素的连分数的对数的线性型的下界估计,该文对一类以整数幂为元素的连分数对数的线性型下界给出了估计.
文献[8]给出了下面的定理:
定理A设{an}是给定的正整数列,α与β是用连分数定义的函数
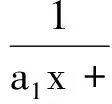
在两个不同的正整数点的值.
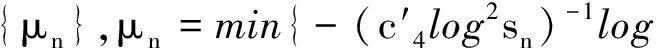
i)μ(x)=μn,n=1,2,…;
ii)μ(x)在区间[n,n+1]上是线形函数.
用μ*(x)表示μ(x)的反函数.
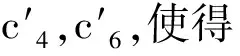
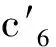
其中A=max{λ(μ*(logH+1)+1),λ(μ*(logH+1)+2)}.
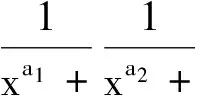
设x1,x2∈N*,1 p1(x)=1,q1(x)=xa1,p2(x)=xa2,q2(x)=xa1+a2+1, pn(x)=xanpn-1(x)+pn-2(x),qn(x)=xanqn-1(x)+qn-2(x) (n≥3), (1) α=f(x1),β=f(x2). 如所知[9] (2) 容易看出,对于n=2,3,…,有 (3) 由式(1)得到 以及 (4) 同理,有 证明需证明对于任意不全为零的正整数k,l, logsnlogqn+1=logqnlogsn+1. (6) 由式(1)有 (7) (8) 于是,若引理结论不成立,则由式(6)-(8),得到 (9) 其中 由式(4)及式(5),有估计 (10) (11) 由式(9)-(11)以及假设条件得到 这是一个矛盾,从而引理结论得证. 引理2[1,10]设α1,…,αn;β1,…,βn是两组代数数,αi不为0或1,βj不全为0,用logαi表示对数主值,记 m=degQ(α1,…,αn),H=max{|β1|,…,|βn|,e},Ti=max(H(αi),e),1≤i≤n. 若Λ=β1logα1+…+βnlogαn≠0,则 |Λ|≥exp(-(16mn)2(n+2)logT1…logTnlogH). |Λ|=|klogα+llogβ|>exp(-c0log2snlogH)(1-exp(c4log2snlogH+logc3wn)). (12) 证明由引理1,存在只与α,β有关的常数n0,使得当n≥n0时,有 (13) (14) 此外,有 (15) (16) 由式(14),(16)得到 |Λ|>exp(-(c0log2snlogH))-c3Hwn. (17) 显然,存在常数c4,使得 c0log2snlogH+logH+logwn+logc3 (18) 由式(17)及式(18),有 |Λ|>exp(-c0log2snlogH)(1-exp(c0log2snlogH+logH+logwn+logc3))> exp(-c0log2snlogH)(1-exp(c4log2snlogH+logc3wn)). 取数列{μn},μn=min{-(c4log2sn)-1logc3wn,-(c4log2sn+1)-1logc3wn+1}.用下面的方式定义数列{μn}的扩展函数μ(x),且μ(x)是递增函数: i)μ(x)=μn,n=1,2,…; ii)μ(x)在区间[n,n+1]上是线形函数. 用μ*(x)表示μ(x)的反函数. 定理1设上面引理3中的假设条件成立,k,l是不全为零的整数,并且 μ(n+1)-μ(n)>1(n≥1),存在常数c0和c4,则有 |Λ|=|klogα+llogβ|>exp(-c0AlogH)(1-exp(-c4A)), 其中A=max{λ(μ*(logH+1)+1),λ(μ*(logH+1)+2)}. 证明以n表示使 μ(n-1) (19) 成立的最小正整数.使用引理2中的记号,可以分两种情况进行考虑. |Λ|>exp(-c0log2snlogH)(1-exp(c4log2snlogH+logc3wn)). (20) 由式(19),得到 |Λ|>exp(-c0log2snlogH)(1-exp(c4log2snlogH+logc3wn))> exp(-c0log2snlogH)(1-exp(c4log2sn(logH+(c4log2sn)-1logc3wn)))> exp(-c0log2snlogH)(1-exp(c4log2sn(logH-μn)))> exp(-c0log2snlogH)(1-exp(-c4log2sn)). (21) 为了叙述简便,引用文献[8]中的符号,记λn=log2sn.由式(19),有 μ*(logH+1)≤n<μ*(logH+1)+1, 结合上式与式(21),并注意到λn→∞(n→∞),给出 |Λ|>exp(-c0λnlogH)(1-exp(-c4λn))> exp(-c0λ(μ*(logH+1)+1)logH)(1-exp(-c4λ(μ*(logH+1)+1))). (22) |Λ|>exp(-c0λn+1logH)(1-exp(c4λn+1logH+logc3wn+1)), 类似于情况I中的证明,同理可以得到 |Λ|>exp(-c0λn+1logH)(1-exp(-c4λn+1))> exp(-c0λ(μ*(logH+1)+2)logH)(1-exp(-c0λ(μ*(logH+1)+2))). (23) 联合式(22)与(23),并注意到λn的定义,便证得此定理结论. [1] Baker A, Wustholz G. Logatithmic forms and group varieties[J]. J Reine Angew Math,1993,442:19-62. [2] Baker A. The theory of linear forms in the logarithms. Diophantine approximations and its applications[M]. New York: Academics Press,1973:1-23. [3] Baker A. Transcendental number theory[M]. Cambridge: Cambridge University Press,1979. [4] 王莉,于秀源.关于∏有理逼近的注记[J].杭州师范大学学报:自然科学版,2008,7(1):9-11. [5] 徐传胜,李红婷,韩振来.数学史和数学课程整合的实现途径[J].山东师范大学学报:自然科学版,2008,23(4):128-131. [6] Zhu Yaochen. The algebraic independence of certain transcendental continued fractions[J]. Acta Math Sinica NS,1991,7(2):127-134. [7] Yu Xiuyuan. A theorem on the transcendence and its applications[J]. Science in China(A),1997,40(8):826-831. [8] 于秀源,沈忠华.连分数对数的线性型下界[J].数学年刊,2009,30A(3):353-358. [9] 华罗庚.数论导引[M].北京:科学出版社,1986. [10] Diophantine. Approximations, diophantine equations, transcendence and applications[J]. Indian Jour of Pure and Applied Math,2006,37:9-39.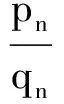
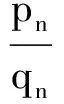
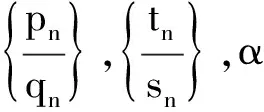
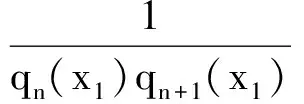
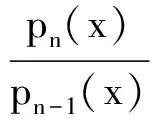
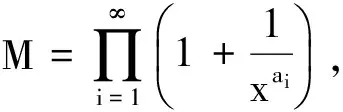
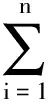
2 引 理
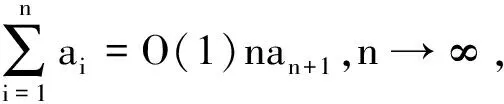
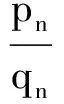
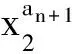
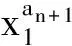
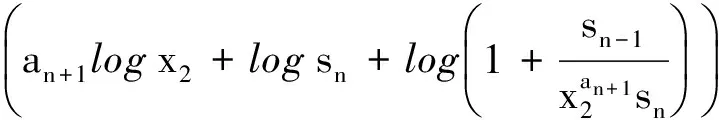
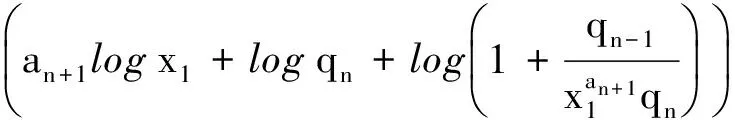
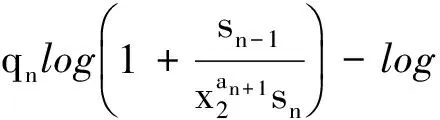
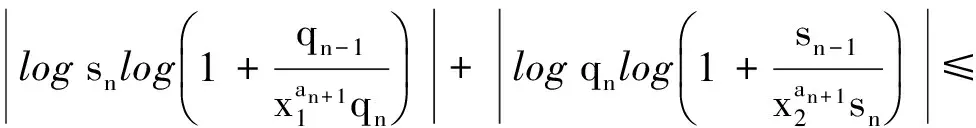
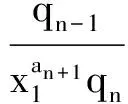
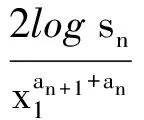
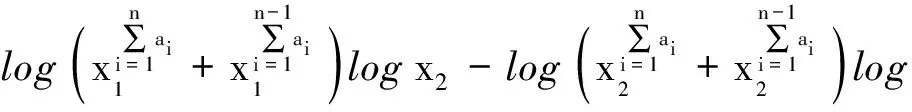
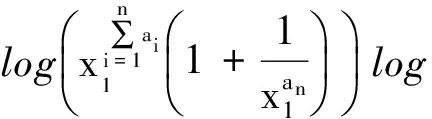
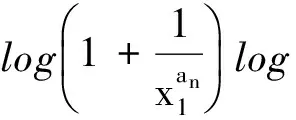
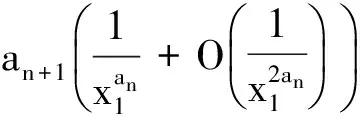
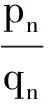
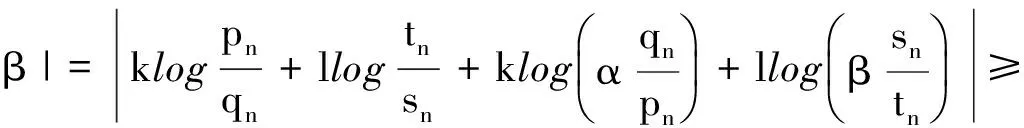
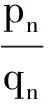
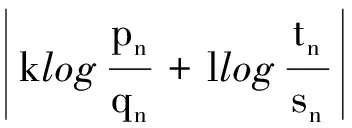
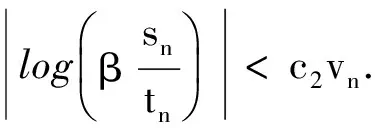
3 定理及证明