Some Properties on ω-Stage Euclidean Ideals

WU Zhong-lin

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

1 Introduction

LetRbe a ring. A norm overRis defined as a function

φ:R→N∪{0}

satisfying the following conditions:

1)φ(a)≥0 for alla∈R.

2)φ(a)=0 if and only ifa=0.

Ak-stage division chain (k∈N) for any arbitrary elementsa,b∈R,a≠0, is understood as the sequence of equalities

b=aq1+r1,
a=r1q2+r2,
⋮
rk-2=rk-1qk+rk.

Suchk-stage division chain is called terminating ifrk=0.

A ringRis calledω-stage Euclidean ring with respect to the normφ, if any arbitrary elementsa,b∈R,a≠0, there exists ak-stage division chain for somek, such thatφ(rk)<φ(a). Since the above sequence of equalities shows the Euclidean[1-2]algorithm

φ(r1)<φ(a),
φ(r2)<φ(r1),
⋮
φ(rk)<φ(rk-1),

thenφ(rk)<φ(a) implies the fact

φ(rk)<φ(rk-1)<…<φ(r1)<φ(a).

Examples ofω-stage Euclidean rings are the ringZof integers, the ringF[x] of polynomials. In [3], there are manyω-stage Euclidean rings that are not Euclidean in the usual sense. For instance,R(n) isω-stage Euclidean whennis equal to 14, 22.

2 ω-Stage Euclidean Ideals

Definition1[4]LetRbe a ring. For two elementsa,b∈R, if there exists an elementc∈Rsuch that

a=bc.

Thenbis said to dividea. We denote it byb|a.

For two elementsa,b∈R, if there exists an elementd∈R, such that

1)d|a,d|b;

2) For anyc∈R,c|a,c|b⟹c|d;

Thendis called the greatest common divisor ofaandb, and denote it bygcd(a,b)=d.

In this article, we introduce the concept ofω-stage Euclidean ideal.

Definition2LetAbe an ideal of a ringR. If there exists a mapφ:A→N∪{0} such that

1)φ(x)≥0 for allx∈A. Moreover,φ(x)=0 if and only ifx=0.

2) For anya,b∈A,a≠0, there exists ak-division chain for somek,

b=aq1+r1,
a=r1q2+r2,
⋮
rk-2=rk-1qk+rk,

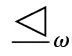
3 The Main Results

Theorem1LetAbe an ideal ofR. ThenAis anω-stage Euclidean ideal if and only if for arbitrary elementsa,b∈A,a≠0, there exists a terminatingk-stage division chain for somek.

ProofSufficiency: The last remainder in a terminating division chain is 0, and satisfies

φ(rk)<φ(a).

Thus, for arbitrary elementsa,b∈A,a≠0, there exists a terminating division chain. HenceAis anω-stage Euclidean ideal ofR.

Necessity: Assume thatAis anω-stage Euclidean ideal ofR. For arbitrary elementsa,b∈A,a≠0, there exists ak-stage division chain for somek,

b=aq1+r1,
a=r1q2+r2,
⋮
rk-2=rk-1qk+rk,

such thatφ(rk)<φ(a). Ifrk=0, then the chain has terminated. Ifrk≠0, then consider the pair (rk-1,rk). For some integert, there exists at-stage division chain starting from (rk-1,rk),

rk-1=rkqk+1+rk+1,
rk=rk+1qk+2+rk+2,
⋮
rk+t-2=rk+t-1qk+t+rk+t,

such thatφ(rk+t)<φ(rk). Ifrk+t=0, then the chain has terminated. Ifrk+t≠0, then process the pair (rk+t-1,rk+t). This yields

…<φ(rk+t)<φ(rk)<φ(a).

After a finite number of application, there will reduce a terminating division chain from the pair (a,b).

Proposition1LetAbe anω-stage Euclidean ideal ofR. Then for arbitrary elementsx,y∈A,x≠0, there exists the greatest common divisor for (x,y).

ProofIfy=0, thengcd(x,y)=x. Ify≠0, then by Theorem 1, there exists a terminating division chain from (x,y). Letrk=0,

x=yq1+r1,
y=r1q2+r2,
⋮
rk-3=rk-2qk-1+rk-1,
rk-2=rk-1qk.

By the last equation, we haverk-1|rk-2. Fromrk-3=rk-2qk-1+rk-1, we getrk-1|rk-3. Analogously, this yieldsrk-1|x,rk-1|y. Supposem|xandm|yfor an elementm∈A. By the first equation, we getx-yq1=r1,m|r1. The second equation impliesm|r2. Continuing the process, this yieldsm|rk-1. Hence,gcd(x,y)=rk-1.

Theorem2Everyω-stage Euclidean ideal of a ring is principal .

ProofLetAbe anω-stage Euclidean ideal ofR. IfA={0}, thenA=(0). IfA≠{0}, then there exists at least a nonzero element inA. SinceAis anω-stage Euclidean ideal, there exists a mapφ:A→N∪{0}. Let the setM={φ(x)|x∈A,x≠0}. Obviously,M≠∅, there exists a minimal number inM, and we denote it byφ(a), 0≠a∈A. SinceAis anω-stage Euclidean ideal, then for anyb∈A, there exists a terminating chain

b=aq1+r1,
a=r1q2+r2,
⋮
rk-2=rk-1qk+rk.

such thatφ(rk)<φ(a). By Euclidean algorithm, we have

φ(rk)<φ(rk-1)<…<φ(r1)<φ(a).

Sinceφ(a) is the minimal number inM, then this forcesφ(r1)=0. Hencer1=0. In other words, the chain must be terminated in the first row. Thereforeb=aq1∈(a), we haveA⊆(a). On the other hand,a∈AandAis an ideal, so (a)⊆A. This yieldsA=(a). ThereforeAis principal, as desired.

Example1LetR=Z[x]/(x2)={a+bx|a,b∈Z,x2=0}. ThenRis not anω-stage Euclidean ring. ButI1={bx|b∈Z,x2=0} is anω-stage Euclidean ideal ofR.

ProofAssume thatRis anω-stage Euclidean ring. Then every ideal ofRis anω-stage Euclidean ideal. Choose

I2={2m+nx|m,n∈Z,x2=0}.

I2=R(2p+qx),

wherep,q∈Z. We choose (2+0x), (0+1x)∈I2, then there exista+bx,c+dx∈R, such that

2+0x=(a+bx)(2p+qx)=2pa+(qa+2pb)x⟹2pa=2,qa+2pb=0,
0+1x=(c+dx)(2p+qx)=2pc+(qc+2pd)x⟹2pc=0,qc+2pd=1.

We getp≠0 andc=0. Hence

qc+2pd=2pd=1.

Sincep,d∈Z, this yields a contradiction. HenceRis not anω-stage Euclidean ring.

However,I1={bx|b∈Z,x2=0} is anω-stage Euclidean ideal ofR.

Let the ringZof integers be anω-stage Euclidean ring with respect to the normφ. We define a map overI1:

φ:I1→N∪{0},

It is easy to show that

1)φ(nx)=φ(n)≥0 for allnx∈I1.

2)φ(nx)=0⟺nx=0.

For anyax,bx∈I1,ax≠0, we havea,b∈Z,a≠0. SinceZis anω-stage Euclidean ring, there exists ak-division chain for somek,

b=aq1+r1,
a=r1q2+r2,
⋮
rk-2=rk-1qk+rk,

such thatφ(rk)<φ(a). This yields

bx=axq1+r1x,
ax=r1xq2+r2x,
⋮
rk-2x=rk-1xqk+rkx,

such thatφ(rkx)=φ(rk)<φ(a)=φ(ax). Therefore,I1is anω-stage Euclidean ideal ofR.

Theorem3LetAbe anω-stage Euclidean ideal of a ringR. Then everyn×nmatrix overAcan be reduced to a canonical diagonal matrix by elementary transformation.

wheredi∈A.

ProofLetM=(aij)∈Mn(A). Ifa11≠0, then consider the first column

SinceAis anω-stage Euclidean ideal of a ringR, thena11anda21have a finite division chain. By successive row operations we may reduce the form

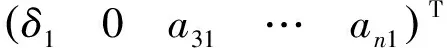
whereδ1is the greatest common divisor for (a11,a21), Now work onδ1anda31. Continue untila31,…,an1are reduced to 0,…,0. Nowδn-1will be a common divisor ofa11,a21, …,an1.

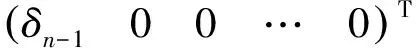
To the first row, we reducedMto the form similar to the first column

whered1∈A.

Ifa11=0, then the element of the upper left corner may turn into a nonzero element by row (column) elementary transformations. Similarly, we get the above diagonal form as well.

Continuing the process,Mis further reduced to the form

wheredi∈A. Hence, the theorem is proved.

[1] Cohn P M. On a generalization of the Euclidean algorithm[J]. Proc Cambrige Phil Soc,1961,57:18-30.

[2] Samuel P. About Euclidean rings[J]. J Algebra,1971,19:282-301.

[3] Cooke G. A weakening of the Euclidean property for integral domains and applications to algebraic number theory[J]. J Reine Angew Math,1976,282:133-156.

[4] Hungerford T W. Algebra[M]. New York: Springer-Verlag,1974.