高维空间中一类正多面体的构造与其体积

林 磊

(华东师范大学数学系,上海 200241)

高维空间中一类正多面体的构造与其体积

林 磊

(华东师范大学数学系,上海 200241)

确定了在n维欧几里德空间中两向量间夹角均大于等于90度的非零向量组中向量的最大个数,进而确定了向量间夹角大于90度时的最大个数.由此导出了n维欧几里德空间中正n+1面体的构造与其体积公式.

正n+1面体;体积;n维欧几里德空间

在2006年华东师范大学攻读硕士学位研究生入学试题《高等代数》中有这样一道填空题:

如果α1,α2,…,αm是n维欧几里德空间中一组非零向量,且满足(αi,αj)≤0,∀i≠j,则m的最大值是___________.

我们首先来给出这道题的解答.

解 m的最大值是2n.

设m的最大值是t.令e1,…,en是n维欧几里德空间V的任一规范正交基,即该组基满足(ei,ej) =δi,j,i,j=1,…,n,则取V中2n个非零向量±e1,±e2,…,±en.容易看出这一向量组满足题目的要求,于是得t≥2n.

下面我们通过对维数n用数学归纳法来证明t=2n.

n=1时.若至少存在3个满足性质的非零向量α1,α2,α3∈V,则因dimV=1,故存在非零k,l∈,使得α2=kα1,α3=αl1.由于

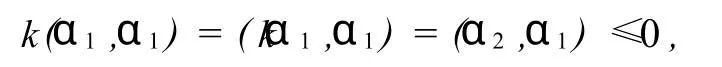
而(α1,α1)＞0,因此k＜0.同理得l＜0.于是,(α2,α3)=kl(α1,α1)＞0,这与条件(α2,α3)≤0相矛盾.故t≤2,从而t=2.于是,n=1时结论成立.

假设n=k-1时结论成立,我们要证n=k时结论也成立(k＞1).由上面的讨论可知,只要证明在V中不存在2k+1个非零向量α1,α2,…,α2k+1,使得(αi,αj)≤0,∀i≠j.假设α1,α2,…,α2k+1是V中满足性质的非零向量组,令α=α2k+1,W=(α)⊥,则W是V的k-1维子空间.设βi是αi在W中的正交投影,i=1,2,…,2k,则存在ki∈,使得αi=βi+kαi,i=1,2,…,2k.由于

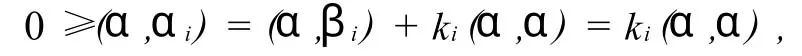
故ki≤0.某些βi可能等于0,由于αi≠0,故此时必有ki＜0.若存在i≠j,使βi=βj=0,则(αi,αj) =(kiα,kjα)=kikj(α,α)＞0,矛盾.故至多只能有一个βi等于0.不妨设β1,β2,…,β2k-1均不为0,则由于

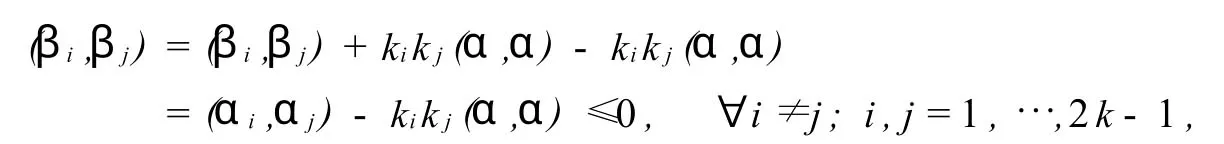
所以β1,β2,…,β2k-1是k-1维欧几里德空间W中满足性质的非零向量组.但是由于这些向量共有2k-1个,这就与n=k-1时的归纳假设相矛盾.于是这样的2k+1个非零向量α1,α2,…,α2k+1不存在,故n=k时结论也成立.由数学归纳法知,该结论对任何n都成立.

如果将上述问题中不同的向量间的内积“≤0”的条件改为“＜0”,情况会更加有趣,而讨论将更为复杂.

命题1 设α1,α2,…,αm是n维欧几里德空间V中的向量,满足(αi,αj)＜0,对任意i≠j,则m的最大值等于n+1.

证先证在V中存在满足命题条件的n+1个向量.从而得m的最大值大于等于n+1.我们对V的维数n用数学归纳法来构造性地证明满足命题条件向量组的存在性.

当n=1时,设α是V的基,则α1=α,α2=-α就是满足条件的向量组.

假设n=k-1时满足条件的向量组存在,现在来考虑dimV=n=k＞1的情形.在V中任取一单位向量,记作αk+1.考虑W=(αk+1)⊥,则W是k-1维的欧几里德空间.根据归纳假设,在W中存在k个向量β1,…,βk,使得(βi,βj)＜0,对任意i≠j成立.于是,这些向量均非零,所以,不妨设它们都是单位向量.令则a＞0.取实数l,使得0＜l＜a,则对任意i≠j,有 l2＜-(βi,βj).取αi=βi-lαk+1,i=1,…,k,则

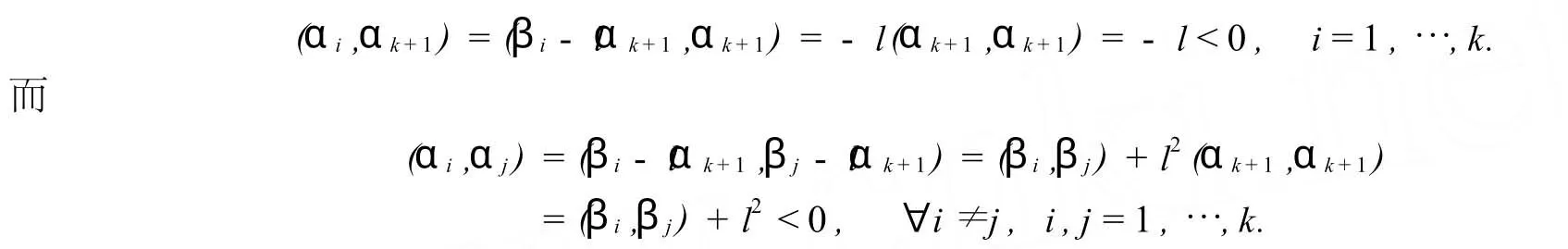
从而α1,…,αk,αk+1就是满足条件的向量组.于是,由归纳假设知,对任意的n维欧几里德空间V,存在满足条件的向量组.

下面我们仍对V的维数n用数学归纳法来证明V中满足命题条件的向量组最多只有n+1个,从而证得命题.

对于1维欧几里德空间,设α是V的基,αi=liα,i=1,2,3是V中任意3个非零向量,则非零实数l1,l2,l3中必有两个数是同号的,不妨设它们是l1,l2,从而(α1,α2)=l1l2(α,α)＞0.于是,在V中不存在向量个数大于2的满足条件的向量组.

假设V的维数等于k-1时,不存在k+1个满足条件的向量组.考虑dimV=k＞1时的情形.用反证法.假设V中存在k+2个非零向量β1,…,βk+2,满足(βi,βj)＜0,对任意i≠j.令W=(βk+2)⊥,则W是V的k-1维子空间.令αi为βi在W上的正交投影,i=1,…,k,k+1,则βi=αi-lβik+2,其中li∈,i =1,…,k,k+1.由于(βi,βk+2)=(αi-lβik+2,βk+2)＜0,故li＞0,i=1,…,k,k+1.若有某个αi=O,则存在另一j≠i,使得(βi,βj)=(-lβik+2,αj-lβjk+2)=lilj(βk+2,βk+2)＞0,这与假设矛盾.因此,α1,α2,…, αk+1是W中的非零向量组,且(αi,αj)=(βi,βj)-lilj(βk+2,βk+2)＜0,对任意i≠j,i,j=1,…,k+1.这与维数等于k-1时的归纳假设相矛盾.从而易得:当V的维数等于k时,不存在k+2个满足命题条件的非零向量.由数学归纳法得结论成立.

事实上,我们还有比命题1更强的结论.

命题2 在n维欧几里德空间V中,存在n+1个单位向量α1,…,αn+1,使得对任意i≠j,(αi,αj)= -

证该命题的证明与上述命题中存在性部分的证明相近.仍对V的维数n用数学归纳法.

当n=1时,设α是V的任一单位向量,则α1=α,α2=-α即满足要求.

假设当n=k-1时结论成立,则当n=k＞1时,任取一单位向量α∈V,考虑W=(α)⊥,在k-1维欧几里德空间W上,由归纳假设,存在k个单位向量β1,…,βk,使得(βi,βj)=-,对任意i≠j.取则

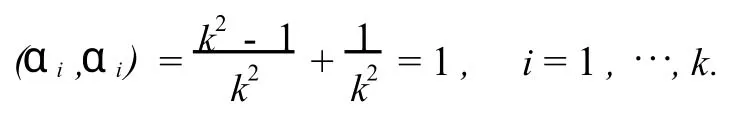
设P0P1…Pn是n维欧几里德空间中的一个正n+1面体,则该正多面体的顶点间的距离都是相同的.故可取P1(1,0,…,0),P2(0,1,…,0),…,Pn(0,0,…,1).可知它们任两点间的距离相等,都等于2.现设P0=(a,a,…,a),则由|P0P1|=|P1P2|=2得

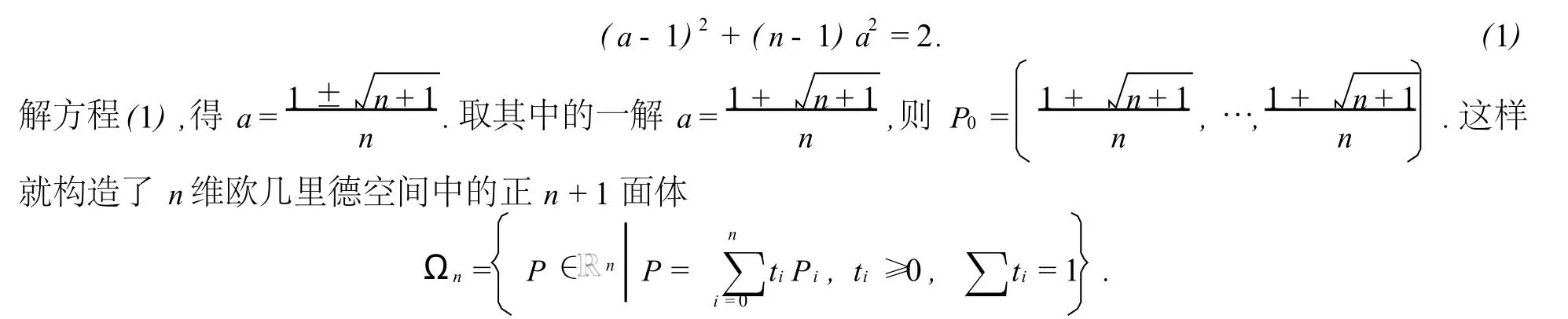
为计算Ωn(在n中)的体积,先考虑由向量确定的平行2n面体Ω的体积|Ω|.由n级行列式的几何意义(参见[2,P97])得,Ω的有向体积等于下列行列式D的值

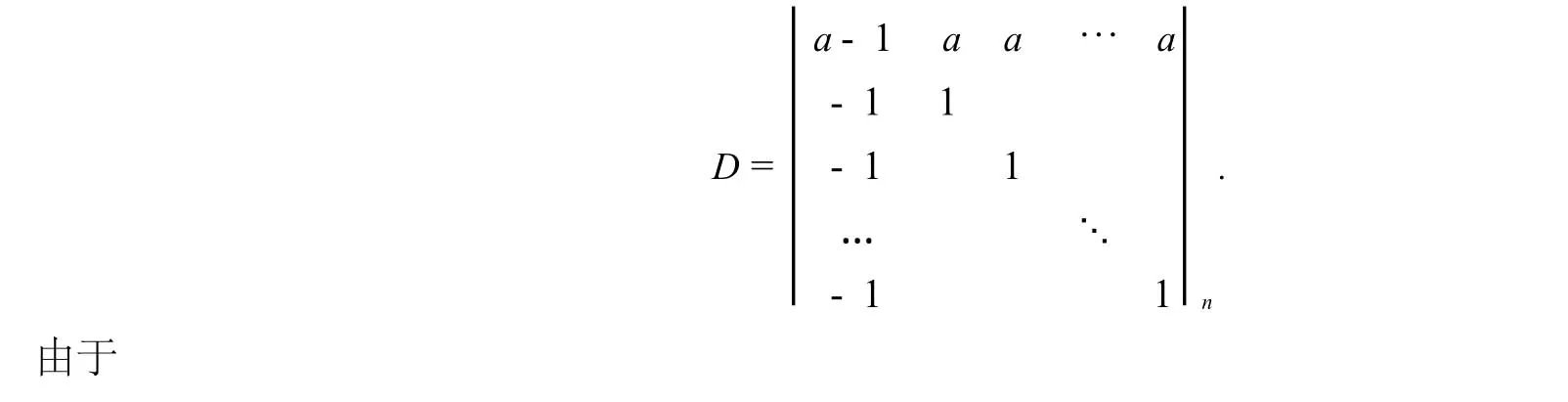
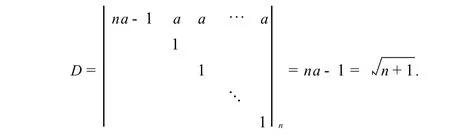
或等价地,因为Ωn就是n维空间中由P1,P2,…,Pn,P0张成的单纯形,所以根据[3,P319]中关于单纯形的体积公式,其体积为

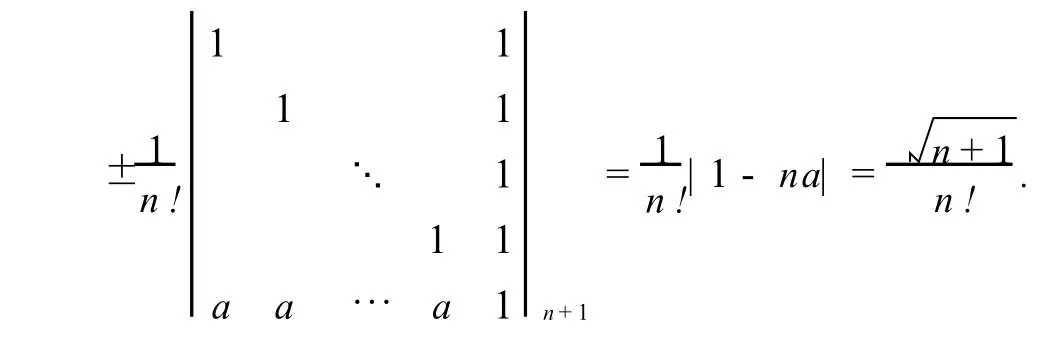
由于正n+1面体Ωn的棱长等于2,于是我们有

定理3 在n维欧几里德空间中,棱长为a的正n+1面体的体积

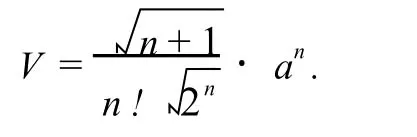
最后考虑一些特例:取n=2,在平面上,边长等于a的正三角形的面积等于a2.取n=3,在三维空间中,棱长等于a的正四面体的体积等于在四维空间里,棱长等于a的正五面体的体积等于.而在七维空间中,棱长等于a的正八面体的体积等于注意到此时a7的系数为有理数.

[1] 日本数学会.数学百科辞典(第2版)(中译本)[M].北京：科学出版社,1984.

[2] 陈志杰.高等代数与解析几何(上册)[M].北京：高等教育出版社,2000.

[3] 数学手册[M].北京：高等教育出版社,1979.

O151.24

C

1672-1454(2010)03-0181-04

2007-10-30

上海市重点学科(B407)以及国家级精品课程“高等代数与解析几何”建设项目资助