不同温度亚微米粒子扩散运动的实验研究

杨 蒙,王昊利,韩 巍

(中国计量学院计量测试工程学院,浙江杭州310018)

过去二十多年来,微电子机械系统(MEMS)在科学研究和工业生产领域得到了巨大发展和广泛应用.由于在化学、生命、医学、机械、电子、计算机、能源、热学等领域中的广泛应用,作为微电子机械系统重要分支的微流体流动和传热问题已成为研究热点.到目前为止,多种方法用于微流体流动和传热问题的研究,其中实验研究仍然占有重要地位.由于微流体装置中微通道的特征尺度在0.1～100 μ m,传统的流动与传热测量工具已无能为力,直到可视化测量技术的出现才解决了这一难题[1-6].目前,测量分辨率最高且最具代表性的微尺度全流场可视化测量技术当属微流体粒子图像测速技术(micro-PIV),它是在大尺度PIV技术上发展而来的.大尺度PIV技术目前应用已经非常广泛,如凃程旭等人利用PIV技术开展了圆柱绕流的实验研究[7],但对于Micro-PIV而言,仅有10年左右的发展时间.1998年,Santiago等人在原有大尺度PIV技术基础上首先发展了Micro-PIV技术,并利用100～300 nm粒径的荧光示踪粒子测量了120 μ m×120 μ m Hele-Shaw 盒子的表面张力驱动流,整体速度为50 μ m/s[8].利用micro-PIV技术可以分析在不同温度下微通道中微纳米粒子的扩散运动.近年来,国内外进行了许多代表性的粒子扩散运动的理论及实验研究.Olsen和Adrian理论研究了布朗运动对micro-PIV相关信号峰值的影响[9].Hohreiter等提出了一种新技术,利用示踪粒子布朗运动会引起互相关函数峰值扩散的原理来进行温度测量[10].Park等人实验测量了500 nm粒子布朗运动和温度的关系,测得二维布朗运动的精度为4.26%[11].Seok和Sang利用大数值孔径的显微物镜获得了荧光示踪粒子的全场布朗运动图像,布朗运动现象明显[12].王绪伟和李战华实验观测了200 nm荧光粒子的布朗运动,利用单粒子追踪(SPT)算法获得粒子的均方位移,实验扩散系数为2.09×10-12m2/s,比理论值偏小约5%[13].王昊利提出了一种基于纳米粒子群布朗运动图像分析的微流体温度测量算法,探索微流体温度场的测量方法[14].最近,Aloke等人提出了一种光学扩散仪技术,并将其应用到生物试剂检测中[15].利用粒子图像追踪测速(PIV/PTV)技术,研究粒子位移的空间和时间演化过程,可以从细节上了解亚微米粒子扩散规律.基于此,本文利用micro-PIV/PTV可视化测量技术研究了18℃(室温)到70℃不同温度下,方形槽道内粒径为520 nm的荧光示踪粒子热扩散运动规律.

1 实验系统

实验采用德国 LaVison公司生产的micro-PIV系统,系统照片及原理图如图1.Micro-PIV系统包括美国New Wave公司生产的Nd:YAG 15 mJ双脉冲激光器、Lavision公司生产的图像增强型CCD相机(像素数为1376×1040)、同步控制器以及由高性能三坐标轴控制器和显微物镜组成的MITAS显微平台.被测对象为520 nm荧光示踪粒子(Thermo ScienTIF;%95%94ic公司),示踪粒子按照1∶150的体积比与去离子水混合成粒子溶液注入边长为5 mm、深度1 mm的有机玻璃方形槽中.为了研究不同温度下亚微米粒子的扩散运动,本文设计安装了一个温控电加热系统,包括电加热板、热电偶和温控仪.温控仪接收热电偶的温度信号,从而控制固定在通道上表面的电加热板的开关,以此来实现对水温的控制与调节,方槽及温控系统如图2.

图1 micro-PIV系统照片(a)和测量原理图(b)Figure 1 Micro-PIV system(a)and measurement schematic(b)

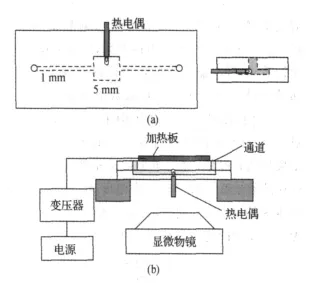
图2 热电偶和电加热器及控制系统示意图Figure 2 Setup of thermocouple and electrical heater(a)and electrical heating system of temperature control(b)

实验中,532 nm激光对荧光粒子进行照明,粒子发射出610 nm(红色)的荧光,分别经过L D Plan-Neofluar 20×0.40 NA型显微物镜和荧光滤色镜,由CCD相机获得不同时刻的示踪粒子跨帧运动图像.整个实验的硬件驱动、数据采集、图像分析及速度矢量计算由micro-PIV系统提供的DaVis 7.2软件完成.

2 粒子图像与速度矢量计算

实验过程中,水溶液温度控制在18℃(室温)到70℃之间,为了获得粒子运动的统计规律,每个温度下拍摄80对粒子图像.相邻两帧粒子图像的时间间隔 Δ t设定为分子运动的近似时间尺度30 ms[16].图3给出了其中一幅粒子图像,可以看到所采集520 nm的粒子图像拍摄清晰,是进行粒子运动速度场分析的重要基础.

图3 520 nm粒子图像Figure 3 Particle images of 520 nm

在本文的研究中,为实现不同温度下亚微米粒子扩散运动分析,须对任一时刻的粒子运动进行追踪测速,获得每个时间间隔的粒子运动的位移.为实现这一方法,采用DaVis软件所提供的粒子图像和粒子追踪混合算法(PIV/PTV)计算全部粒子的运动速度.PIV/PTV算法的主要思路为利用粒子图像相关算法跟踪单个粒子的运动获得粒子运动速度.为了准确识别粒子,需设定粒子图像尺度和灰度范围,将单个粒子与背景噪音准确区分,同时对跨帧图像中的粒子进行正确配对.DaVis软件中的粒子探测方法是,寻找到粒子最大灰度值的位置并在此位置周围设定边长为粒子直径大小的判读区域,通过两帧粒子的相关性获得每个粒子的速度值.由于粒子追踪算法不适合高浓度粒子溶液,因此实验中的粒子溶液配比设定为1∶150.图4给出了某一个时刻粒子速度矢量图,可以看到,所获得的粒子速度的长度和运动方向呈现明显的随机特征,由此可见 520 nm粒子受水分子作用产生了明显的布朗运动现象.粒子速度场的计算为研究亚微米粒子扩散运动提供了定量分析基础.

图4 速度矢量Figure 4 Velocities evaluated by PIV/PTV algorithm

3 粒子扩散实验结果与分析

本文通过计算粒子的空间均方位移的方法对粒子扩散运动进行分析.根据所获得的速度场,首先按照式(1)计算出每个示踪粒子的位移平方值

式(1)中ri为第i个粒子的位移,ui和vi分别是该粒子在X和Y方向的速度分量.

由于在同一温度下测量条件恒定不变,所以不同时刻粒子的位移平方应该有相同的分布规律.本文以291 K(18℃)和 323 K(50℃)两个温度为例进行说明,其余温度情况类似.随机选取两个温度下拍摄的三对图像计算粒子的位移平方,并取对数分布结果,由图5给出.从图中可以看到,大约有3500个测量点的位移平方的对数值分布于-16到-10.5之间,除了位于-11到-10.5之间的粒子存在少量偏差外,绝大多数的粒子数据分布基本相同,表明相同温度下不同时刻粒子扩散运动具有统计不变性.

图5 相同温度下粒子位移平方值的对数分布:(a)T=291 K,(b)T=323 KFigure 5 Distributions of logarithm of square displacement of particles under the same temperature:(a)T=291 K,(b)T=323 K

图6给出了从291 K(18℃)到343 K(70℃)温度下,粒子数Np关于位移平方对数值的直方图.图中,X轴为位移平方的对数,Y轴为粒子数.可以看到,任一温度下的粒子位移呈现类正态分布特征,粒子的位移平方的对数值分布于-16到-11之间,而粒子数主要集中于-13和-12两点.当位移平方的对数值为-13时各温度下的粒子数均达到峰值,这与单个粒子布朗运动的均方位移的数量级一致.例如,当温度为291 K时,由Stokes-Einstein公式(2)计算得到的单个粒子在无限空间中的均方位移为0.98×10-13m2[17].

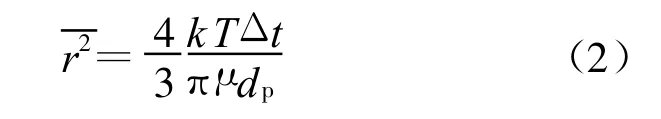
图6 不同温度下粒子位移平方对数的直方图Figure 6 Histogram of the particles number distributions in terms of SD under different temperatures

从图6中我们还能够看到,不同温度下粒子数分布情况不同.当位移平方的对数值不大于-13时,粒子数随着温度的升高而减少(除-13点因测量误差等原因303 K温度下的粒子数略低于313 K);而当位移平方的对数值大于-13时,粒子数则随着温度的升高而增加.这一统计规律表明随着温度的升高粒子的扩散能力得到增强.

式(3)中,〈r2〉为空间均方位移,N为粒子总数.需要指出的是,公式(3)中的空间均方位移〈r2〉与公式(2)中的均方位移有着不同的含义.前者是一对图像中所有粒子的位移在空间上的平均值,而后者是单个粒子在在其所有的运动时间内位移的时间平均值.图7给出了粒子空间均方位移与温度之间关系的实验值与拟合曲线.可以看到,空间均方位移随着温度的升高而线性增大.

为了定量说明粒子扩散能力与温度之间的关系,本文提出采用空间均方位移来研究粒子扩散运动的强度,由式(3)给出:

图7 空间均方位移(SMSD)与温度的关系Figure 7 Relationship between the spatial mean square displacement(SMSD)and the temperature

由于实验技术的限制,目前很难对100 nm左右及以下尺寸的粒子运动进行跟踪观察,多是研究悬浮液及悬浮气体中不同粒径的粒子的含量.粒径较大的粒子在悬浮液中受到重力沉降作用的影响,主要表现出粒子的沉降,而非粒子的扩散运动.例如,对于悬浮液而言,粒径为500 nm的粒子由于布朗扩散与重力沉降在1 s内平均位移(μ m)之比为1.05∶0.138;而粒径为10 μ m时,该比值为0.24∶55.4,扩散的影响可忽略不计[16].

4 结 语

本文利用micro-PIV/PTV技术对不同温度下方形通道中520 nm粒子的扩散运动进行了实验研究,并通过PIV/PTV混合算法计算得到了粒子运动速度和位移平方的对数分布.利用空间均方位移的概念分析了一定数量亚微米粒子的扩散运动问题.结果表明,相同温度不同时刻的粒子位移平方分布一致,位移平方的对数分布于-17～-11之间,呈现类正态分布特征.粒子空间均方位移值随着温度的升高而线性增大.以上结果对于利用亚微米粒子热扩散特性获取微小尺度液体温度分布提供了研究思路.

[1]GAD-EL-HAK M.The fluid mechanics of microdevices—T he Freeman Scholar Lecture[J].Fluids Eng,1999,121:5-33.

[2]HO C M,TAI Y C.Micro-Electro-Mechanical sy stems(MEMS)and fluid flows[J].Annu Rev Fluid M ech,1998,30:579-612.

[3]王昊利,王 元.Micro-PIV技术——粒子图像测速技术的新进展[J].力学进展,2005,35(1):77-90.

[4]WERELEY S T,MEINHART C D.Recent advances in micro-particle image velocimetry[J].Annu Rev Fluid Mech,2010,42:557-576.

[5]WERELEY S T,WILLERT C E.Particle Image Velocimetry[M].Berlin:Springer,2007,241.

[6]ADRIAN R J.Twenty years of particle image velocimetry[J].Exp Fluids,2005,39:159-169.

[7]凃程旭,王昊利,林建忠.圆柱绕流的流场特性及涡脱落规律研究[J].中国计量学院学报,2008,19(2):98-102.

[8]SANTIAGO J G,WERELEY S T,MEIN HART C D.A particle image velocimetry system for microfluidics[J].Ex p Fluids,1998,25(4):316-319.

[9]OLSEN M G,ADRIAN R J.Brownian motion and correlation in particle image velocimetry[J].Optics&Laser T echnology,2000,32(8):621-627.

[10]HOHREIT ER V,WERELEY S T,CHUNG J N,et al.Cross-correlation analysis fo r temperature measurement[C]∥In Proceeding of the 4th International Symposium on Particle Image Velocimetry.Germany:Gö ttingen,September,2001:17-19,134-138.

[11]PA RK J S,CHOI C K,KIHM K D.T emperature measurement for a nanoparticle suspension by detecting the Brownian motion using optical serial sectioning microscopy[J].Meas Sci Technol,2005,16:1418-1429.

[12]SEOK K,SANG J L.Measurement of 3D laminar flow inside a micro tube using micro digital holographic particle tracking velocimetry[J].Micromech Microeng,2007,17:2157-2162.

[13]王绪伟,李战华.SP T方法在纳米粒子布朗运动观测中的应用[J].实验流体力学,2008,22(1):84-87.

[14]WANG H L.Algorithm of measurement for microfluidic temperature by using micro-piv technique[J].Acta Metrologica Sinica,2008,29(4A):1-4.

[15]KUMAR A,GORTI V M,SHANG H,et al.Optical diffusometry techniques and applications in biological agent detection[J].Fluid Eng,2008,130:111401-1-8.

[16]严宗毅.低雷诺数理论[M].北京:北京大学出版社,2002:179.

[17]EINSTEIN A.On the motion,required by the molecularkinetic theory of heat of particles suspended in a fluid at rest[J].Ann Phys Lpz,1905,17:549-560.