混合次分数布朗运动下交换期权的定价

徐 峰，李润泽

(1.苏州市职业大学 商学院，江苏 苏州 215104；2.湖南大学 经贸学院，湖南 长沙 410006)

随着期权定价模型研究的不断深入，不少学者开始考虑用修正的分数布朗运动来描述股票价格的变化行为，如次分数布朗运动。T.Bojdecki等[1]、C.Tudor[2-3]先后研究了次分数布朗运动，并指出次分数布朗运动具有分数布朗运动类似的许多性质，如自相似性、增量相关以及长记忆性等。由于次分数布朗运动的这些性质，所以用次分数布朗运动也可以刻画股票价格的行为模式。Yan Litan等[4]给出次分数布朗运动下的Itô公式，并将之推广到多维的情形。肖炜麟等[5]给出了次分数布朗运动下带交易费用的备兑权证定价的公式，并通过数值模拟检验了长记忆性对定价结果有显著的影响。N.C.El等[6]引入一个新的过程，即混合次分数布朗运动，它是由一个次分数布朗运动和一个布朗运动共同构成的线性组合，并证明在次分数布朗运动和布朗运动独立的情况下，当Hurst参数H∈(3/4，1)时，混合次分数布朗运动是一个半鞅，等价于布朗运动。为了刻画金融资产的长记忆性，本文假定股票价格遵循混合次分数布朗运动过程，利用随机分析理论，得到混合分数布朗运动环境下交换期权价格所满足的Black-Scholes偏微分方程，并通过求解该偏微分方程，给出了交换期权的定价公式.本文假定1/2＜H＜1。

1 混合次分数型Itô公式

在这一部分，将文献[4]中给出的次分数型I t ô公式推广到混合次分数型I t ô公式。记则过程{X(t)│t≥0}为混合次分数布朗运动，它的一些性质参见文献[6]。

定理1 假定且，均属于L2(P)，则有

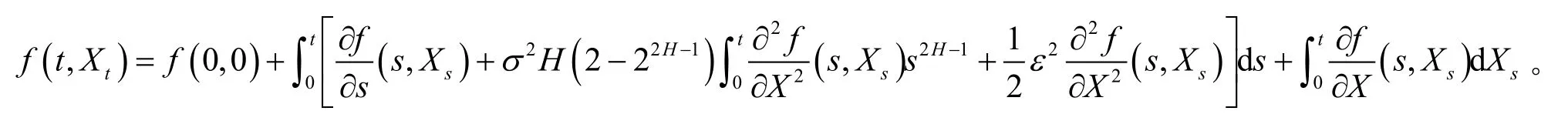
证明 由于根据泰勒展开并整理可得

由于，所可以近似地认为且和Bt独立，所以，代入式(1)并忽略高阶无穷小，则有

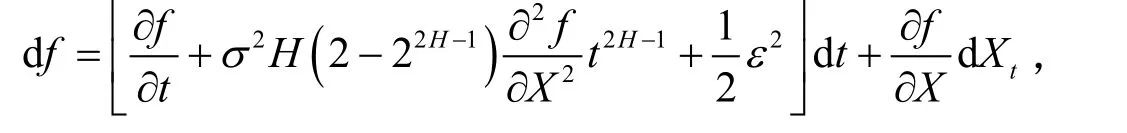
从而定理1成立。

2 混合次分数布朗运动环境下交换期权的定价模型

假设金融市场中有3种证券，1种是无风险资产，即债券，其价格满足

2种是风险资产，如股票，i种风险资产的价格满足

式(3)中：r，μi，σi，εi(i=1，2)为常数；BH(t)为概率空间(Ω，F，P)上的Hurst参数为H的次分数布朗运动；B(t)为布朗运动，这里假设BH(t)和B(t)相互独立。

定理2 随机微分方程(3)的解为

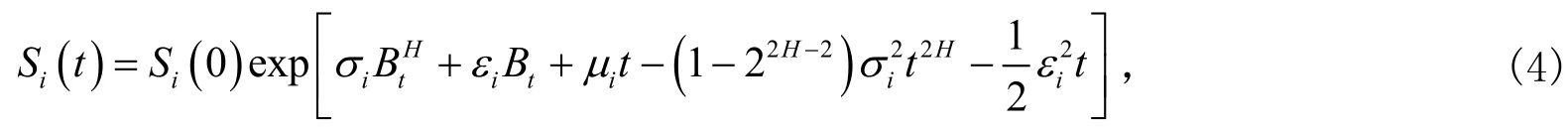
式中i=1，2。

证明 记

定理3 假设 F (⋅ ,⋅,⋅)∈ C1,2,1(R × R × R →R)是未定权益的价值过程，则混合次分数布朗运动环境+下的Black-Scholes偏微分方程为

证明 假设 Ft=F( t , S1,S2)，由定理1和定理2有

构造一个自融资投资策略，则财富过程从而

比较式(6)和式(7)可得

根据可得从而定理3得证。

3 模型的求解

交换期权可视为T时刻到期的未定权益下面给出混合次分数布朗运动环境下交换期权的定价公式。

定理4 假设股票价格满足式(3)，到期日为T，则交换期权V(t，S1，S2)在任意t时刻的价格为

证明 由定理3知，交换期权的价格V(t，S1，S2)满足偏微分方程(5)，即初始条件为

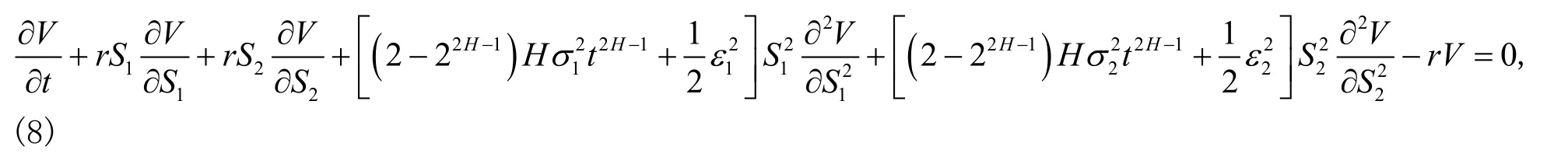
下面采用变量替换将式(8)转化成一个Cauchy问题，令通过计算得

将上式代入式(8)并整理可得

令x=lnZ，则式(9)可以写成

进一步地，令U(Z，t)=u(η，τ)，η=x+α(t)，τ=ρ(t)，则有

将式(11)代入式(10)，则有

假设

则有

将式(13)代入式(12)，则有

式中边界条件为

根据热传导方程经典解理论，方程(14)存在唯一强解

通过计算可得

将变量反代入即可证得定理4成立。

4 结论

本研究采用混合次分数布朗运动刻画股票价格的变化过程，研究混合次分数布朗运动环境下交换期权的定价模型，通过求解偏微分方程得到了期权定价公式的显式解。该模型也可应用于研究其他期权的定价，如利差期权、亚式期权等。

参考文献：

[1]BOJDECKI T，GOROSTIZA L G，TALARCZYK A.Sub-fractional Brownian motion and its relation to occupation times[J].Statistics and Probability Letters，2004，69：405-419.

[2]TUDOR C.Some properties of the sub-fractional Brownian motion[J].Stochastics，2007，79(5)：431-448.

[3]TUDOR C.Inner product spaces of integrands associated to sub-fractional Brownian motion[J].Statistics and Probability Letters，2008，78(14)：2201-2209.

[4]YAN Litan，SHEN Guangjun，HE Kun.Itô′s formula for the sub-fractional Brownian motion[J].Communication on Stochastic Analysis，2011，5(1)：135-159.

[5]肖炜麟，张卫国，徐维军.次分数布朗运动下带交易费用的备兑权证定价[J].中国管理科学，2014，22(5)：1-6.

[6]EL N C，ZIL I M.On the sub-mixed fractional Brownian motion[J].Appl.Math.J.Chinese Univ.，2015，30(1)：27-43.