正规乘积算符积分法及其应用的教学探讨

夏立新陈翠云袁盼盼

(1．河南科技大学 物理系,河南 洛阳 471003；2．河南科技大学 艺术学院,河南 洛阳 471003)

0. 言

在量子力学中，算符的不对易给量子系统的数学处理带来了复杂性与困难，有什么方法能使普通数与算符在数学处理上的差距缩小呢? 如何把量子力学中抽象的符号法变得浅显易懂，变得更实用呢? 这是我们需要研究的课题。

在符号表示方法上，突出的是狄拉克,通过结合薛定谔波函数的物理思想，他开创性地引入了态矢这一概念，并建立了q数与态矢的关系。在此基础上，狄拉克进一步用抽象的方式直接处理一些有重要意义的物理量。狄拉克的符号法不只是非常有用的数学方法，更为重要的是它能深入事物的本质，可用简洁精炼的方式来表达物理规律。在物理观念上, 符号法对量子力学的发展具有革命性的贡献[1]。

从狄拉克提出符号法以来,符号法已引起了许多研究者的关注[2-6]。特别是范洪义教授，他从解决积分系统地建立了有序算符积分法理论，他相继出版了三部重要的学术专著[2-4]，为符号法的发展做出了贡献，取得了重要的成果。在看似已非常完善的量子力学理论体系中，解决了多年来悬而未决的若干问题，开辟了一个全新的研究方向，发展了量子力学的表象与变换理论[2]。该积分法在量子光学、群表示论、固体理论，耦合振子动力学、Wigner函数、经典力学向量子力学的过渡、统计力学、相干态与压缩态等方面发挥了积极的作用。在有序算符积分法的基础上，范教授也系统地建立了量子力学的纠缠态表象，并介绍了它在量子光学、固体物理、热场动力学和量子场论等方面的应用[3]。同时，范教授进一步地建立了量子力学的连续纠缠态表象，使量子光学的数理基础理论得到了更新的发展，对相干态、压缩态、相位算符，以及量子主方程等理论都有崭新的阐述，深化了量子纠缠的思想。还给出了若干纠缠态表象、量子幺正变换等变换理论，促进了对傅利叶光学理论的研究[4]。

本文主要介绍了量子力学中玻色子算符正规乘积算符的积分方法。特别是，对正规乘积算符积分法及其应用的教学给出了简单的探讨。在量子力学的教学中，期望该积分法引起广泛的关注，它有利于培养学生发现问题和解决问题的能力。

1.规乘积及其性质

对于波色子算符a和 a+，由其所构成的任何函数或算符f( a,a+)，可写为

其中，j,k,l,⋅⋅⋅,m是正整数或零。利用算符a和a+的对易关系[ a, a+]=1，可将任意算符(1)中的产生算符 a+都移到所有湮灭算符a的左边，这时，我们称算符 f( a,a+)已被排列成了正规乘积形式，并用︰︰标记。算符的正规乘积在量子场论、量子光学、固体物理等理论的描述中都被广泛采用。算符有序乘积有三种常见的形式，分别为正规乘积、反常乘积和对称乘积。其中，正规乘积具有非常重要的性质，它们是发展狄拉克的符号法以及表象理论的重要形式[1]。本文以正规乘积为例。首先，我们参考文献[2-4]写出八条正规乘积的性质，它们给出如下

① 正规乘积内，玻色子算符相互对易。

② 对于c数(普通数)，它可自由出入正规乘积记号。

③ 对于正规乘积内的c数，可进行积分(或微分)运算，只要积分是收敛的。

④ 正规乘积内部的函数的和差可以分拆,即,︰W±V︰ =︰W︰±︰V︰。

⑤ 厄米共轭操作可进入︰︰内，也就是，

(︰W⋅⋅⋅V︰)+=︰(W⋅⋅⋅V)+︰。

⑥ 正规乘积内的正规乘积记号可以取消；或在︰︰内部的任意两个算符(相邻或不相邻的)紧外边可以加上正规乘积记号。

（2）菌种驯化将活化后的乳酸菌接种到山羊乳中训化增殖，依次调整菌种接种量为8%，4%，2%，40℃恒温培养至凝乳，保证菌种活力能在4 h内凝乳。

⑦ 正规乘积内，以下两个等式成立：

对单模情形，表示为

在教学中，我们要逐一地将这八个性质详细地介绍给学生，让他们能够很好地理解，并能灵活运用它们。

2.本算符的正规乘积表示

这一节，我们介绍两个基本算符的正规乘积表示。首先，给出真空投影算符00的正规乘积展开形式

这是容易证明的。根据文献[2]的方法，由粒子态的完备性，可得

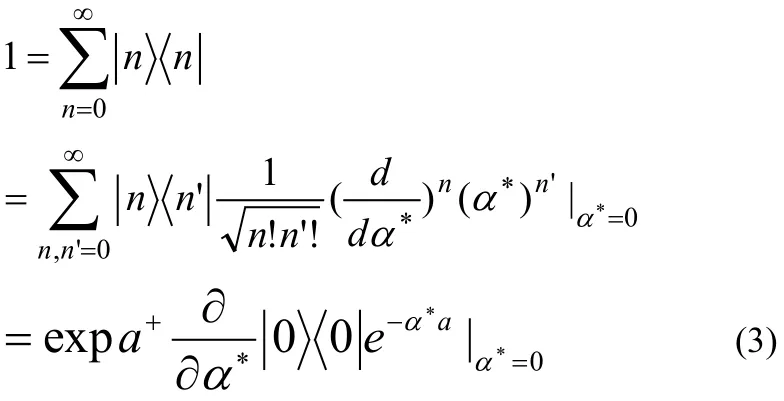
在具体的计算中，公式(2)和(6)是两个重要算符的正规乘积表示。在教学中，不仅要介绍给学生，同时还要学生会证明。证明过程对理解算符正规乘积的性质是很有帮助的。

3.规乘积算符积分法

对于玻色算符, 正规乘积算符积分法，这个理论充分注意并应用了正规乘积的性质，其基本思想[2-4]可表述为：利用正规乘积内部玻色算符相互对易的特点,只要把原本并不对易的玻色算符变为正规乘积形式，就可在对互不为共轭量的投影型积分算符积分时，可把算符视为互相对易的(c数)参量，这样，积分就可以顺利进行。最后，把积分结果取消其正规乘积形式，从而可恢复算符明显的不对易性。

在教学中，最好用一个简单的例子来说明正规乘积算符积分法，这样使学生更容易理解。

上面，只说明了正规乘积积分法。算符的排序还有反正规乘积和对称乘积，相应的就有反正规乘积和对称乘积积分法，有兴趣的读者可参考文献[2-4]。上述三种积分法可统称为有序乘积积分法。

4.单应用

为了对正规乘积算符积分法有一个更深的认识, 本节中，我们举文献[2]中的两个例子来说明该积分法的应用。

其中, ︰e−a+︰a的左边是产生算符,右边是湮灭算符。因此，整个被积的算符函数已被排成正规乘积。所以，可把左边的︰移到第一个指数左边，并把右边的︰移到第三个指数的右边。根据性质①，玻色算符在︰︰内对易,三个exp指数函数的指数可直接相加，(8)式变成

5.束语

总之，本文介绍了正规乘积算符积分法及其应用的教学探讨。正规乘积算符积分法使狄拉克的符号法更完美、更具体，而且能更好地表达物理规律。

在教学中，正规乘积算符积分法的关键是如何利用正规乘积算符的八个性质，以及两个基本公式(2)和(6)。符号法知识的教学是非常重要的，期望该积分法引起广泛的关注，它有利于本科学生加强基本功、扩大知识面，以及有利于培养他们发现问题和解决问题的能力。

[1]P.A. Dirac, The Principle of Quantum Mechanics[M], Oxford:Oxford University Press，1958.

[2]范洪义,量子力学表象与变换论----狄拉克符号法进展[M],上海:上海科学出版社, 1997.

[3]范洪义,量子力学纠缠态表象及应用[M],上海:上海交通大学出版社,2001.

[4]范洪义,从量子力学到量子光学---数理进展[M],上海:上海交通出版社,2005.

[5]W.Y. Louisell,Quantum Statistical Properties ofRadiation[M],New York:John Wiley Press,1973.

[6]M.O. Scully, M.S. Zubairy, Quantum Optics[M], Cambridge:Cambridge University Press, 2000.