大跨径混凝土箱梁桥腹板受力研究

王 涛

预应力混凝土箱梁桥以其特有的优点,如整体性能好、结构刚度大、变形小、抗震性能好等被人们广泛的采用。目前预应力混凝土连续箱梁桥在大多数情况下均采用三向预应力结构,这就使箱梁腹板的受力变得极其复杂,而如果对箱梁腹板上的主拉应力控制不当,使主拉应力超过允许值,则会引起腹板的斜裂缝。腹板斜裂缝的出现是箱梁桥跨中下挠的主要原因,而且斜裂缝的存在在很大程度上还影响到了桥梁的美观,承载能力和使用寿命,严重的还会影响到交通安全。

1 腹板主拉应力的理论计算分析

预应力混凝土受弯构件由作用(或荷载)短期效应组合和预加力产生的混凝土主拉应力,应按下列公式计算[1]:

其中,σcx为在计算主应力点,由预加力和按作用(或荷载)短期效应组合计算的弯矩Ms产生的混凝土法向应力;σcy为由竖向预应力钢筋的预加力产生的混凝土竖向压应力;τ为在计算主应力点,由预应力弯起钢筋的预加力和按作用(或荷载)短期效应组合计算的剪力带产生的混凝土剪应力;当计算截面作用有扭矩时,尚应计入由扭矩引起的剪应力;对后张预应力混凝土超静定结构,在计算剪应力时,尚宜考虑预加力引起的次剪力;σpc为在计算主应力点,由扣除全部预应力损失后的纵向预加力产生的混凝土法向预压应力,按本规范公式计算;y0为换算截面重心轴至计算主应力点的距离;n为在同一截面上竖向预应力钢筋的肢数;σ′pe,σ″pe分别为竖向预应力钢筋、纵向预应力弯起钢筋扣除全部预应力损失后的有效预应力;Apv为单肢竖向预应力钢筋的截面面积;sv为竖向预应力钢筋的间距;b为计算主应力点处构件腹板的宽度;Apb为计算截面上同一弯起平面内预应力弯起钢筋的截面面积;S0,Sn分别为计算主应力点以上(或以下)部分换算截面面积对换算截面重心轴、净截面面积对净截面重心轴的面积矩;θp为计算截面上预应力弯起钢筋的切线与构件纵轴线的夹角。

2 有限元模型的建立

2.1 工程背景

包头镫口黄河特大桥(55+9×100+55)m变截面连续箱梁桥,该桥梁结构的基本资料如下:主梁采用单箱单室变截面预应力混凝土箱梁。该桥桥面为双向2%的横坡,桥面单向纵坡为0.742 5%。箱梁顶板宽12.75 m,底板宽7 m。顶板厚30 cm,底板厚 30 cm～55 cm,腹板厚35 cm～55 cm。主墩采用矩形截面,高10.25 m。在主墩两侧2.5 m处分别设置两个直径为800 mm的钢管混凝土作为临时支撑,施工阶段主梁和主墩铰接。该桥采用三向预应力体系,采用公路一级荷载设计标准。

2.2 有限元模型的建立

采用空间三维结构模型,将主梁模拟为空间梁单元。全桥共建节点67个,共划分单元64个。其成桥结构计算简图如图1所示。

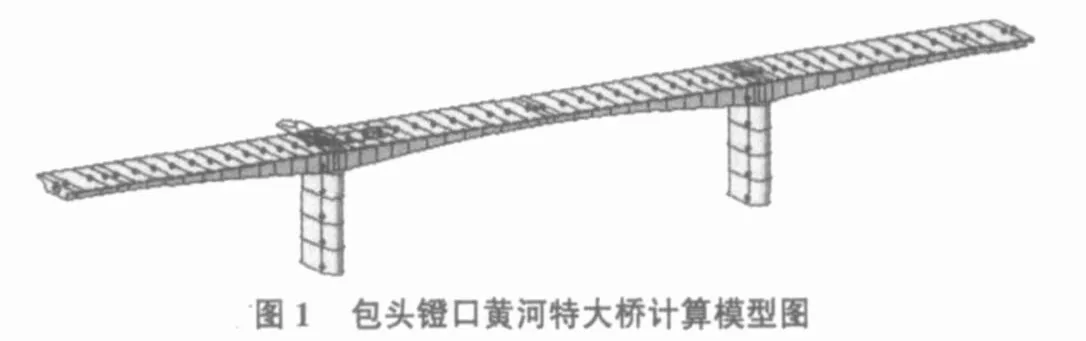
2.3 材料常数的确定

通过现场采样对混凝土的弹性模量进行试验,试验结果确定混凝土的弹性模量 Ec=35GPa,混凝土容重按规范取γ=25 kN/m3,预应力钢绞线弹性模量 Ep=195 GPa,混凝土泊松比 vc=0.2。

2.4 预应力损失摩擦系数和每米局部偏差系数的确定

通过现场进行的对顶板束和腹板束的预应力损失试验,其中预应力管道为塑料波纹管。确定预应力损失摩擦系数 u=0.17,每米局部偏差系数k=0.003 6。

2.5 计算荷载的确定

1)结构自重:把每个单元的重量折算成在该段上的均布荷载,作用在该单元上。

2)预应力作用:直接在有限元软件内输入钢束布置形状和钢束预应力荷载。

3)挂篮前移:等效成一个弯矩加到节点上。该弯矩等于挂篮自重乘以挂篮移动的距离。

4)解除临时支撑:将支撑拆除以前的所有工况的支撑内力进行叠加,就得到解除支撑前的内力。解除支撑后,用一个和支撑内力相反的集中力作用在支撑位置上。

5)二期恒载:将二期恒载等效成沿桥纵向的均布荷载作用在单元上。

6)活载:用公路一级荷载进行计算。

7)混凝土的徐变:计算成桥后1 500 d的徐变,其中徐变系数取2.39。

3 腹板受力计算结果

3.1 应力计算值与实测值比较

两个控制截面在各施工阶段下梁顶和梁底纵向正应力的计算值和实测值的比较见图2。

3.2 腹板受力计算结果

箱梁腹板的纵向正应力和剪应力由有限元软件Midas-Civil计算得到,其中腹板纵向正应力取梁顶和梁底纵向正应力的平均值。跨中1/4截面在各施工阶段和活载及徐变作用下的主拉应力值见表1(压为正,拉为负)。

表1 截面腹板主拉应力计算表 MPa

4 结语

本文通过现场的实际测量和计算分析得出以下结论:

1)由上面应力计算值和实测值的对比可以看出,各控制截面在各个施工阶段中的计算值和实测值的最大应力差均在0.5 MPa之内,验证了用该有限元软件建模进行仿真应力分析是十分可靠的。

2)在成桥后1 500 d徐变作用下,中跨1/4截面,它和梁根处的剪应力相差不大,但由于它的竖向预应力筋间距大,竖向压应力就小,且其纵向正应力也比梁根处小。根据有关理论分析,腹板斜裂缝往往就出现在1/4跨附近。

3)竖向预应力筋对控制和减小主拉应力起到很大的作用。

4)由表1中对主拉应力的计算结果来看,主拉应力值都在规范允许值之内,为该桥在运营过程中的安全可靠性提供了坚实的理论依据。

[1]贺拴海.桥梁结构理论与计算方法[M].北京:人民交通出版社,2003:146-201.

[2]王勖成,邵 敏.有限单元法基本原理和数值方法[M].第2版.北京:清华大学出版社,1996:531-540.