软土中细长桩稳定性分析

朱荣芳

桩基为埋置于土体中的结构物,其侧向受土体约束,稳定性比地面以上的受压构件要好得多,通常不容易失稳。然而,处于软基地段的桩基,由于其侧向约束差且桩基长细比相对较大,就有可能发生失稳,使结构丧失承载能力,最终导致结构破坏。特别在沿海地区,部分段落软土层厚度超过30 m,桩长超过60 m,在这种情况下,细长桩的稳定性问题就不容忽视。

1 细长桩稳定性分析过程

1.1 桩基的边界条件

通常情况下,如果桩底嵌固于岩层且岩性好,可以认为桩底无位移,桩底约束为固结;如果持力层为强风化层或黏土层,桩底可能有微小的位移,宜按铰接考虑。桩顶与桥墩墩柱相接,如果相接处设置系梁或承台,且系梁或承台周围土的抗力较大,可以认为桩顶约束为固结;如果不设系梁或承台,桩顶就有一定量的位移,当桩周土抗力较小时(如淤泥层),桩顶接近于无约束;如果桩周土抗力较大(如黏土层),则桩顶线位移比较小,且存在角位移,可近似按铰接处理。桩基的边界条件不同,其挠曲线方程就不一致。本文为说明其计算方法,采用相对简单的模式进行分析,即假定桩顶、桩底约束均为铰接。在工程实践中,应根据实际情况确定边界条件。当边界条件发生改变时,只要修改挠曲线方程,其他计算过程是类似的。

1.2 桩周土的弹性抗力

利用温克尔假定,认为土体的侧向抗力集度与桩基的挠度成正比,即 q1=k×y(k为比例系数)。

1.3 桩基的挠曲线方程

对于两端铰接的压杆,可假定其挠曲线为正弦曲线:

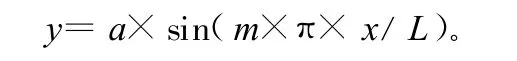
其中,L为桩长。

由于桩基受侧向土约束,各区段的幅值(反弯点间的水平位移极大值a)随桩基埋深成递减趋势,不可能是常量。如果取挠曲线方程为:

上式计算结果会精确些,但会大大增加计算工作量。本文为简化计算,选用形式相对简单的挠曲线方程。即:

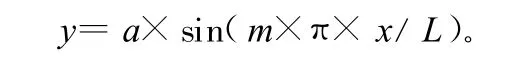
其中,L为桩长。

其一阶导数:

令 u=m×π×x/L,当 x=0时,u=0;当 x=L时,u=m×π。

进行变量代换后积分得:

2)桩顶垂直力所做的负功。

令 u=m ×π×x/L,当 x=0时,u=0;当 x=L时,u=m×π。

进行变量代换后积分得:

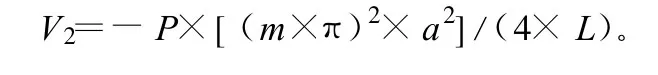
3)桩顶弯矩所做的负功。

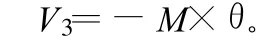
其中,M 为桩顶弯矩;θ为桩顶转角,θ=y′|x=L=a×(m×π/L)。

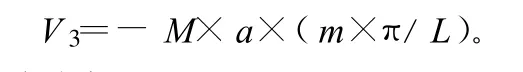
4)桩身弯曲应变能。

令 u=m ×π×x/L,当 x=0时,u=0;当 x=L时,u=m×π。

进行变量代换后积分得:

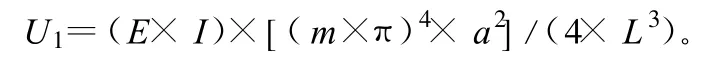
5)桩周土的应变能。

由于桩基通常穿越多种土层,各土层的比例系数 k也不一致,所以要分段进行积分。现假定桩基共穿过n种土层,土层厚分别为 L1,L2,…,Ln,各土层分界处坐标分别为X0,X1,…,Xn,如图2所示。

则桩周土的应变能:

现计算一般项:

其二阶导数:

在实际设计时,可多取几项正弦函数进行叠加,提高计算精度。当桩基的边界条件改变时,应修改挠曲线方程。

1.4 计算过程

计算图如图1所示。

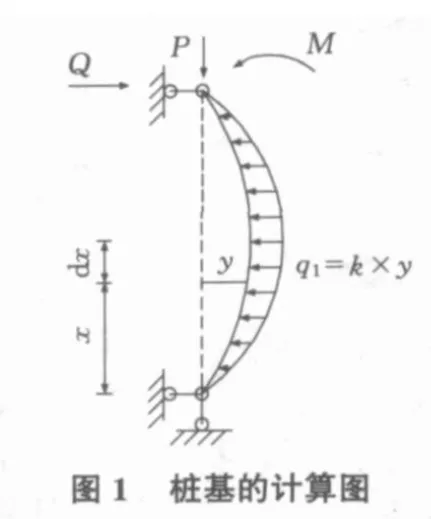
桩基的外力势能主要是桩顶垂直力、桩顶弯矩和桩身自重所做的负功。桩顶剪力对桩基临界荷载影响很小,故略去不计。桩基的应变能为桩基弯曲应变能与土体应变能之和。桩基的总势能等于外力势能与应变能之和。根据势能最小值原理,可计算桩基的临界荷载。现分项计算如下:

1)桩身自重所做的负功。

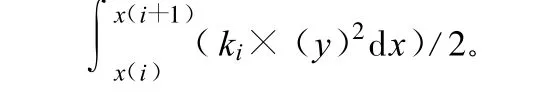
令u=m×π×x/L,当 x=0时,u=0;当 x=L时,u=m×π。

进行变量代换后积分得:

将各项求和,即求出桩周土的应变能。

6)桩基临界荷载的确定。

桩基的总势能等于以上各项之和,即:

上式只有两个未知量:a和m。根据势能最小值原理,当结构处于稳定状态时,总势能为最小值。

令d∏/d a=0,d∏/d m=0,可列出两个方程。

而根据a和m不可能等于零的条件,可求出桩基临界荷载PCR。

2 实例计算

淮安市南昌路大桥主桥为100 m下承式系杆拱,主墩为三柱式桥墩,下接承台、钻孔灌注桩基础。桩基穿越三层土层,桩顶反力7 500 kN,桩长 65 m,土层高度及土层性质见表1。

表1 土层高度及土层性质表

通过计算可知桩基稳定性满足要求。

3 结语

软基地段细长桩的稳定性是一个不容忽视的问题。桩基临界荷载的计算精度受多种因素的影响:1)除了计算荷载外,桩周土的弹性抗力对桩基稳定性有很大影响。因此,桩周土比例系数的取值是否合适,是否与实际受力状况吻合,直接关系到计算结果的精确度。2)挠曲线方程的选取也是很关键的。本文选正弦曲线(只取一项)拟合桩基的变形,变量偏少,存在一定的误差。而且能量法计算结果总是上限,比实际临界荷载(精确解)大,这是不够安全的。3)施工误差(如构件初始缺陷、尺寸误差等)使构件难以达到理想压杆的要求,因此,有必要对计算结果进行适当折减。4)桩基的边界条件还需要进一步探讨,而边界条件对计算结果有较大的影响。

总之,细长桩的稳定分析是一个相对复杂的问题,要精确计算其临界荷载是相当困难的。虽然如此,能量法可以在一定范围内确定桩基的临界荷载,从而在一定程度上避免了设计的盲目性。

[1]JTJ 024-85,公路桥涵地基与基础设计规范[S].

[2]JTG D63-2007,公路桥涵地基与基础设计规范[S].

[3]崔树琴,殷和平.单桩竖向失稳的密度理论分析[J].山西建筑,2007,33(35):112-113.

[4]李廉锟.结构力学[M].北京:高等教育出版社,1999.