格空间中混合单调算子的不动点定理

孙 洁

(徐州师范大学数学科学学院,江苏徐州 221116)

格空间中混合单调算子的不动点定理

孙 洁

(徐州师范大学数学科学学院,江苏徐州 221116)

利用格结构与半序方法相结合,在(ru0)完备的Archimedean型向量格中讨论算子A=BC耦合不动点的存在性.

向量格;格混合单调算子;耦合不动点

0 引言

1987年,郭大钧和Lakshmikantham.v[1]首次提出了混合单调算子的概念并对它进行了一些研究,得到了一系列的结果,开创了一个新的研究方向.之后,由于混合单调算子不仅对非线性泛函分析的理论研究有重要意义,更由于其重要理论价值在于可以直接解决各种工程技术问题,特别对核物理研究及传染病模型研究有着广泛的应用.因此,国内外研究成果不断涌现[1-3].国内外在研究各种非线性问题时大都使用了两个基本条件,即连续性条件和紧性条件.本文利用半序方法(半序由锥 P导出),在非常弱的紧性条件 ——格拟可分和格列紧条件下,得到了不动点定理.在格空间中,这种格拟可分和格列紧是很容易被满足的.我们把算子A表为A=BC的形式,分别对B和C算子加条件,可以得到格混合单调算子A的不动点.在Banach空间中利用锥理论[1]、半序方法、单调迭代[3]等方法研究混合单调算子.而本文是在(ru0)完备的Archimedean型向量格中对格混合单调算子进行讨论.

1 预备知识

本文总假定 E是(ru0)完备的Archimedean型向量格,P是E中的正元锥.

定义1 设 X是一个半序集,D⊂X.如果存在z∈X,满足

(i)对于任给的 x∈D,都有 x≤z;

(ii)如果 y∈X满足x≤y,∀x∈D,就有 z≤y.

则称 z是D的上确界,记为 z=supD.类似的可以定义下确界infD.

定义2 设 X是一个半序集.如果对 ∀x,y∈X,都存在sup{x,y}和inf{x,y},则称 X是一个格.如果 X是一个格.对 ∀x,y∈X,定义 x∨y和x∧y为

x∨y=sup{x,y},x∧y=inf{x,y}.

定义3 设 E是线性空间,又是半序集.如果半序结构与线性结构相容,即对任给的α,β∈R1,α≥0,β≥0,x1,x2,y1,y2∈E,x1≤x2,y1≤y2都有αx1+βy1≤αx2+βy2,则 E称是一个半序线性空间.如果 E是一个半序线性空间,并且在半序结构下是一个格,则称是一个向量格.

格 E的序区间形式为[x1,x2]={x∈E,x1≤x≤x2}的任何集合,其中 x1≤x2,x1,x2∈E.

定义4 若 E为向量格,对于 x∈P,若对于 ∀n∈N,x,y∈E,有 nx≤y⇒x=θ,则称 E为Archimedean型向量格.

定义5 设 E为Archimedean型向量格,固定 u0∈P{θ},{xn}∈E,x0∈P{θ},若存在数列εn→0,εn∈(0,∞),使得|x-xn|≤εnu0(n ∈N),则称{xn}为(ru0)收敛到 x0,记为若对于任意的ε>0,存在 N=N(ε),使得当 m,n≥N时,有|xn-xm|≤εnu0,则称序列{xn}为(ru0)基本列.若 E中元素的任何(ru0)基本列都是(ru0)收敛的,则称 E为(ru0)完备的Archimedean型向量格.定义6 设 E为Archimedean型向量格,P为E中的正元锥,我们称一个线性算子B:E→E为正线性算子,如果 B(P)⊂ P.

定义7 设 E为序向量空间,E称为向量格(又称Riese空间),即对任意的 x,y∈E,存在它们的上确界sup{x,y}和下确界inf{x,y},并且满足下列代数运算与序相容的条件:(i)对任意 z∈E,由 x≤y可推出x+z≤y+z;(ii)如果 x≥θ,而数λ≥0,则λx≥θ.

给定 E中的正元锥P后,可以在 E中引入半序关系如下:x≤y,如果 y-x∈P.

若 u0∈P{θ},令,使得λ(x)u0≤x≤μ(x)u0}对于 u,v∈X,u≤v,则称为 E的一个序区间.

引理1 设 E为Archimedean型向量格,对任意固定的 u0∈P,{xn}∈E,{yn}∈E.

证明详见文献[4].

满足引理1的 E称为格下的序列相容空间.

定义8 设 X是一个格下的序列相容空间,S是X的一个子集

(i)如果对 S的每一个可数全序子集{xn},都存在{xn}的子列{xni}及 ¯x∈X,使得,则称S是X中的格拟列紧集.

(ii)如果对S的每一个全序子集Δ,都存在Δ的至多可数子集{xn}在Δ中格稠密(即对任给的x∈Δ,都存在{xni}⊂{xn},使,则称 S是X中的格拟可分集.

定义9 若 y-x∈P,则Ay≥Ax,A称为格增算子;若 y-x∈P,则Ax≥Ay,A称为格减算子(不要求A是线性的).

定义10 算子 A:Pu0→Pu0,若对任意的 x,y∈Pu0,t∈(0,1),存在η(t,x,y)>0,使得

则称A为格u0凹凸算子.

在 E×E中令

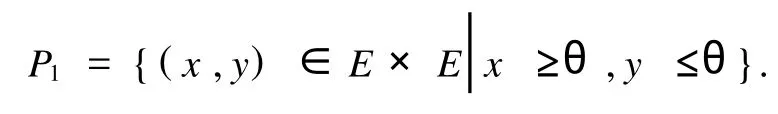
显然,P1是 E×E中的一个锥,并且由 P1导出的半序仍记做“≤”:

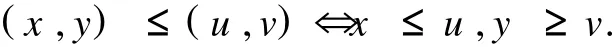
定义算子˜A:D×D→E×E如下:

引理2 A为格混合单调算子,则

(i)˜A在P1导出的半序下为格增算子;

(ii)˜A有不动点(x,y)⇔(x,y)为A的格耦合不动点.

2 主要结果

定理 设 E为(ru0)完备的Archimedean型向量格,D0=[u0,v0]是 Pu0的一个序区间,D=[(u0,v0),(v0,u0)],A:D→Pu0的格 u0-凹凸算子.

(i)存在格下的序列相容的半序空间Y及格混合单调算子B:D→Y和格增算子C:B(D)→Pu0,使得A=CB;

(ii)u0≤A(u0,v0),A(v0,u0)≤v0;

(iii)B(D)是 Y的格拟可分集,格拟列紧集;则A在D中必有格耦合不动点.

令 R2={(y,x)∈D(x,y)∈R1}.设M1是 R1的任意给定的全序子集,M2是 R2的任意给定的全序子集.

由于 B(Mi)(i=1,2)是全序集,故诸 un,vn都有定义,{un}⊂B(M1),{vn}⊂B(M2),并且

由 B(D)是 Y的格拟列紧集和Y为假设可知,un和vn是格收敛的,即存在 u,v∈Y和un,vn使得

且有 un≤u(n=1,2,…),vn≥v(n=1,2,…),由 un,vn的定义可知,对一切 n,有 an≤un≤u,bn≥vn≥v.因{an},{bn}分别在 B(M1)和 B(M2)中格稠密,故对于任何(x,y)∈M1,(y,x)∈M2,序列{an}和{bn}分别存在子序列{ani}和{bnj},使

由 Y为格下的序列相容空间,知

由B为格混合单调算子及(5)式和 Y为格下的序列相容空间,知

于是

故 Cu,Cv有定义,令 ˜u=Cu,˜v=Cv,因 C为格增算子,由(6)式可知,B(x,y) ∈M1,有

即 B(x,y) ≤(˜u,˜v),故 (˜u,˜v) 为 M1的上界.现证 (˜u,˜v) ∈ R1,由 (7) 式及条件(ii) 有

故(˜u,˜v) ∈D.由于{un} ⊂ B(M1),{vn} ⊂ B(M2),故可找到(xnk,ynk) ∈M1,(ynj,xnj) ∈M2,使 unk=B(xnk,ynk)(k=1,2,…)vnj=B(ynj,xnj)(j=1,2,…).

由(˜u,˜v) 为 M1的上界知 ,

故

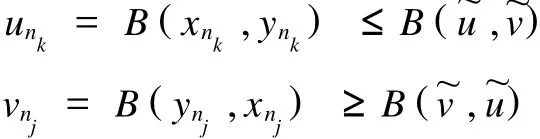
由 (5) 式及 (˜u,˜v) 为 M1的上界可知 u ≤B(˜u,˜v),v ≥B(˜v,˜u),

因此有

故 ˜u,˜v ∈R1,从而(˜u,˜v)为 M1在 R1的上界 ,由 Zorn引理(对向量格空间也成立) 知 ,R1有极大元(u＊,v＊),由(u＊,v＊)≤A(u＊,v＊)和˜A的格增性可知

于是˜A(u＊,v＊)∈R1,故(˜u,˜v)=˜A(u＊,v＊),由引理1,可知(u＊,v＊)为A在D中的格耦合不动点.证毕.

[1] Guo D J,Lakshmikantham V.Coupledfixed pointsof nonlinear operators with applications[J].Nonlinear Analysis,1987,11(5):623-632.

[2] 孙经先.非线性泛函分析及应用[M].北京:科学出版社,2007.

[3] 郭大钧.非线性分析中的半序方法[M].山东:科学技术出版社,1987.

[4] 姚遥.混合单调u0-凹凸算子不动点的存在唯一性[J].淮阴师范学院学报(自然科学版)2008,7(1):5-8.

Fixed Points Theorems of Mixed Monotone Operators In Lattice Space

SUN Jie
(School of Mathematical Science,Xuzhou Normal University,Xuzhou Jiangsu 221116,China)

In this paper,by using the partial order method and lattice theory,we discuss the operatorA=BCin u0-r complete Archimedean vector lattice and the existence of the coupled fixed point.

lattice theory;mixed monotone operators;coupling fixed point

O175

A

1671-6876(2010)04-0283-04

2010-06-18

国家自然科学基金资助项目(10971179);江苏省2010年研究生科研创新计划(CX10S-037Z)

孙洁(1987-),女,江苏宿迁人,硕士研究生,研究方向为非线性泛函分析.

[责任编辑:李春红]