带约束条件多项式的差分代换及其应用

刘保乾

（西藏自治区组织编制信息中心，西藏拉萨850000）

带约束条件多项式的差分代换及其应用

刘保乾

（西藏自治区组织编制信息中心，西藏拉萨850000）

对三角形几何不等式判定算法agl进行了改进和补充，并根据这种算法设计了agl程序的升级版agl2009，讨论了带约束条件差分代换在证明根式型不等式中的应用；给出了用agl程序发现的若干优美的三角形几何不等式.

差分代换；三角形几何不等式；agl算法；机器证明

0 引言

笔者在文献中介绍了2004年12月提出的用增量代换证明锐角三角形不等式的思想[1]，从而产生了带约束条件多项式的差分代换问题.此后又对这种思想做了进一步阐述[2]和改进[3-4]，得到了一种判定三角形几何不等式的算法agl.编写的同名程序对判定三角形几何不等式，尤其是含有角平分线或半角三角函数的不等式十分有效，且在一些方面性能优于Bottema软件[5].本文拟对agl的算法进行改进和补充，并讨论了带约束条件差分代换在证明根式型不等式中的应用.

以下约定：△ABC三边为a、b、c，面积为Δ，角平分线、中线、高、傍切圆半径分别为wa、wb、wc，ma、mb、mc，ha、hb、hc和ra、rb、rc，内切圆和外接圆半径分别为r和R，用∑表示循环和.另外，本文不等式验证环境均在Intel（R）Pentium（R）4 CPU 2.40 GHz，2.41 GHz，1.00 GB内存环境下完成.

1 agl算法的改进和补充

正如文献［3］所述，agl不是一个完备的算法，对一些三角形几何不等式可能失效.在解决这些失效不等式问题的过程中，笔者发现如果对带约束条件的多项式和条件同步进行差分代换，可以部分地解决这个问题.为了保证多项式和条件的同步性，通常将多项式f和条件u≥0写在一起构成一个列表t=[f，u]，称这个列表为一个条件组.显然条件组是由两部分构成，第一部分是多项式部分，用tf标识；第二部分是约束条件部分，用tu标识.为证明不等式f≥0成立，需要用条件u对f按照agl算法进行测试，称这个过程为对条件组t进行正性测试.为了说明agl算法的改进思路，先介绍一下agl算法.

算法agl由文献［3-4］可知，三角形几何不等式的证明，最后可化为条件组w=的正性判定，由于agl算法要进行多项式的相除运算，故需要约定一个主变元，我们约定z是主变元.算法agl的思路就是用w的tu部分去除tf部分差分代换集中的各个多项式，如果得到的商和余式均平凡非负，则可证得不等式f（m，n，z）≥0成立，如果商和余式中仍含有负系数项，则可继续去除，直至得到的多项式中没有负系数项，或者z的次数小于2为止.显然算法agl总是可以终止的.但是要注意，当temp2不为空时，输出的多项式如果是半正定的，则f（m，n，z）≥0一定成立；输出的多项式的正性若不可判定，则f（m，n，z）≥0可能成立也可能不成立，此时agl的算法失效.下面以条件组t=[f，u]为例，说明agl算法的改进思路.

1）对条件组t作差分代换.

2）条件组t的差分代换是一些新的条件组构成的集合S.为了便于叙述和用程序控制，按代换结果的特征和约束条件，可将S中的条件组分成如下几类.

i.如果条件组中tu部分的诸项系数全部为负数，则意味着出现了矛盾的结果（条件u≥0不能满足），称此条件组为矛盾条件组.矛盾条件组应当放弃.出现这种情况的原因是，我们是按照差分代换全集的公式计算S的.以3元为例，多项式f（m，n，z）的差分代换（全集的）计算公式为[6]：在约束条件下，显然z≤m，z≤n不会出现（否则会导出n≥m），这样式（1）中的代换式f（m+z，m+n+z，z），f（m+n+z，m+z，z）就是多余的.

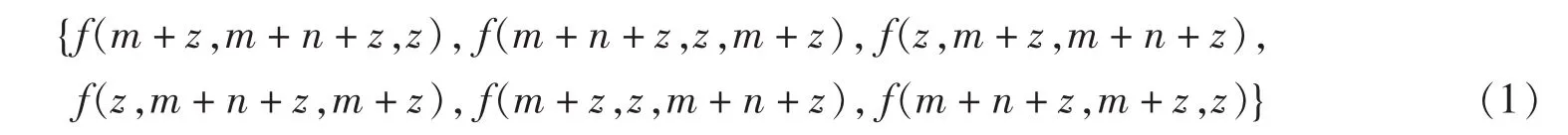
ii.如果条件组中tu部分的诸项系数全部为正数，而tf部分的诸项系数全部为负数，则意味着f≥0不成立，称这样的条件组为反例条件组.显然这里定义的反例条件组是一种极端反例，没有包括tf部分含有正系数项的反例，是最迟出现的反例，这也是本改进算法发现反例效率不高的主要原因之一.

iii.如果条件组中tf部分的诸项系数全部为正数，则称这样的条件组为平凡条件组.

iv.如果条件组中tf和tu两部分的系数均有正有负，则称这样的条件组为待测组.集合中的绝大多数属于待测组.

v.如果条件组中tu部分的系数全部为正，而tf部分的诸项系数有正有负，则意味着这个条件组中tf部分正半定的条件可以扩大为任意正数，从而把条件不等式化为关于正数的不等式，称这样的条件组为正数组.很显然，正数组的条件可以去掉成为普通的多项式不等式，但是否成立仍需要进一步判定.

vi.在算法agl中，由于考虑的是单个条件组的正性判定，tu部分的条件保持不变，故不需要对条件多项式进行检测.但对条件组做逐次差分代换[7]过程中，tu部分要发生变化.如果tu部分主变元最高次的系数出现字母，则多项式相除运算会产生分式，此时可能会产生一些不可预料的结果，这种条件组对agl算法来讲是有瑕疵的.称tu部分主变元最高次的系数出现字母的条件组为瑕疵组.如果出现瑕疵组，则输出相关信息并转入人工处理.

3）对S中符合2）的诸类型条件组进行过滤，以排除极端情形，寻找反例，并转入不同的处理流程.

4）按照agl算法，用待测组中的tu部分对tf部分进行正性测试，如果测试成功，则将该待测组抛弃.

5）对正数组的正性进行机器或人工测试.

6）如果某个待测组的正性不易判定，则可尝试给这个待测组作逐次差分代换，对代换结果再进行测试，以确定正性或进一步寻找反例条件组.

根据上述思路，下面以3元多项式为例，给出agl的改进算法ag.以下用∂（f）表示多项式f的次数.

算法ag算法ag过程如下.

A1）设有3元齐次多项式不等式f（x，y，z）≥0，满足约束条件g（x，y，z）≥0，且∂（g）≤∂（f）.

A2）建立初始条件组[f（x，y，z），g（x，y，z）]，并置入集合变量o中，得条件组集o={[f（x，y，z），g（x，y，z）]}；为保存o变量的状态，同时将o置入temp1中.

A3）对temp1作差分代换，并将代换结果置入temp1之中.

A4）对temp1中的矛盾条件组、平凡条件组进行过滤，剩余部分仍置于temp1中.

A5）检测temp1中的反例条件组，如果有，输出反例并停机.

A6）检测temp1中的瑕疵条件组.

A6.1）如果有瑕疵条件组，则连续做若干次（本文程序中设置为5次）逐次差分代换，并对每次代换寻找反例.若有反例，则输出反例并停机；无反例，则输出人工处理提示信息，停机.

A6.2）如果没有瑕疵条件组，则对temp1中的条件组按agl算法进行正性测试，将测试成功的条件组抛弃，剩余的部分仍置于temp1之中.

A7）检测temp1是否为空集，如果是，则输出不等式成立的信息并停机；如果不是，则转向A3.

可以看出，ag算法的终止性是不能保证的，这是因为：一是ag算法的终止是有缺陷的，这一点可以由A6.1看出，因为对于f（x，y，z）≥0成立但ag无法判定的情形，不可能输出反例，这样程序会进入死循环，为了避免这种情况，程序中设置了测试次数;二是当f（x，y，z）≥0成立但逐次差分代换过程中又没有出现瑕疵条件组时（相当于A6.2时段），程序无法自动终止，此时要强制停机，转入人工处理，这也是ag算法的最大缺点.后面的例11演示了人工处理的例子.

2 三角形几何不等式判定程序agl2009

根据ag算法，笔者编写了三角形不等式判定程序agl2009（源程序见http://www.irgoc.org/viewtopic.php?f=27&t=121&sid=ddaa5759422763f544551e5962898c69或http://www.mathlinks.ro/Forum/viewtopic.php?p=1705932#1705932）.它可以看作是文献［3－4］中agl程序的升级版本，因为它不仅兼顾了agl的功能，而且还增加了许多新功能.

2.1 agl2009程序的功能及命令格式

agl2009是在Maple平台上开发的应用程序，专门对三角形几何不等式进行判定.首先将agl2009拷贝到Maple的安装目录下，在进入Maple环境后就可以运行这个程序.具体运行指令是read`agl2009.txt`，执行了这个指令，就可以使用agl2009了.

auto命令

功能：对一个三角形几何不等式f（△ABC）≥0，作角代换A→π-2A，B→π－2B，C→π-2C，并将代换式化为用三角形边长表示的形式，输出这个代换式的分子w1和分母w2，而且w1和w2已经取掉了平凡非负因式.

指令格式：auto（ineq），其中ineq表示一个待判定正性的三角形几何量表达式.

例1判定wa-ha的正性.判定步骤如下：

＞read`agl2009.txt`；#读入agl2009程序.

＞wa-ha；#键入欲判定不等式表达式.

＞auto（%）；#%表示前次输入的式子wa-ha，即对wa-ha施行auto命令.

执行上述命令后，显示出用双线隔开的两组多项式，前组多项式表示对wa-ha施行角代换后，得到式子的分子和分母；后组表示取掉平凡非负因式后的分子和分母.之所以显示前一组，是为了观察到更多的信息（如不等式的取等号条件等）.

特别值得一提的是，如果w1=0，则预示着发现了一个三角形恒等式.此时程序自动出现“The Inequality may be an identity!”提示.

需要指出的是，auto命令对一些三角形几何量表达式（如含有中线奇次方，根式型几何量和有理式混合等情形）不能自动完成有理化，此时要想办法进行人工有理化.

agl命令

功能：对一个用三角形边长表示的多项式正性进行判定.对不成立者能够自动输出反例条件组；对不能判定者，可以输出一些提示信息.

指令格式：agl（ineq），或者agl（ineq，[ineqs]），其中ineq表示一个用三角形边长表示的多项式；ineqs表示一个条件，目前只能接受aa参数，表示三角形为锐角三角形.

需要指出的是，在agl模块中设置了全局变量o.当程序判定不成功时，变量o能够带出初始条件组的差分代换集，以便于人工进行分析.

qht命令

功能：寻找一些特殊退化条件下取等号的不等式的最佳系数，这个方法是试探性的.这个模块应用了文献[8]提供的恒等式.它本质上是利用了退化三角形＜1，1，2＞，＜1，1，0＞，或者锐角三角形退化为等腰直角三角形.

指令格式：subs（qht，ineq），其中ineq表示一个对应于三角形几何不等式的表达式.

例2确定三角形几何量表达式f1-kf2中可能有的最佳系数，需输入下面的指令:

＞w:=subs（qht，f1-k*f2）；#将所给表达式代换后赋给变量w，以便于调用.

＞solve（subs（x=0，w），k）；#尝试退化条件＜1，1，0＞时可能有的最佳值.

＞solve（subs（x=1，w），k）；#尝试退化条件＜1，1，2＞时可能有的最佳值.

>so lv e（su b s（x=sq rt（2）/2，w），k）；#尝试锐角三角形退化为等腰直角三角形时的情形.

所有这些最佳值得到后，均要用a g l2 0 0 9或其他软件进行验证确认.

e q命令

功能：寻找三角形几何不等式一些特殊的取等号条件.

指令格式：e q（in e q）.注意在用e q找取等号条件时，应通过平方运算尽量将根式化掉.

te stf命令

功能：用三角形边长的经验数据验证不等式.

指令格式：te stf（in e q，[a，b，c]），其中in e q表示不等式对应的表达式，a，b，c表示三角形边长的验证数据.

te stf命令虽然不能判定不等式是否成立，但它作为一个验证命令还是十分有用的.

a g g命令

功能：对单个的条件组按照a g l算法进行测试.如果条件组的正性得到判定，返回-1，否则返回1.

指令格式：a g g（lst），其中lst表示一个条件组.

sd sd命令

功能：对条件组构成的集合进行差分代换，并进行正性测试.

指令格式：sd sd（in e q），其中in e q表示一个条件组集.

a b c to x命令

功能：将一个三角形几何量表达式化为关于正数x，y，z的形式.

指令格式：sd sd（in e q），其中in e q表示一个三角形几何量表达式.

命令a g g、sd sd和a b c to x均是为了方便人工处理而设计的.

2.2 a g l2 0 0 9程序应用举例

例3（文献[9]中的l5 8）在△A B C中，证明

证明用a g l2 0 0 9程序证明如下：

>g:=w b*w c/（2*ra+w a）-2*（b+c）*a*r/（（a+b）*（a+c））；#输入不等式表达式.

>a u to（%）；#由显示的w 1知，不等式（2）有取等号条件b=c.

由于程序对w 1和w 2取平凡非负因式后，均已经是正数，故不等式（2）成立.

由w1的表达式知，不等式（2）有取等号条件b=c，现用e q命令再找一些不等式（2）的取等号条件.输入命令e q（g），则显示：

根据此提示信息可找到不等式（2）的部分取等号条件为{a+c=b}，{b=c}，{a+b=c}.

例4在△A B C中，确定不等式ma≥ha的取等号条件.

解运行e q（m a-h a）命令后，得到部分取等号条件为：

可以看出，第1个取等号条件特别有趣.

例5在锐角△ABC中，证明

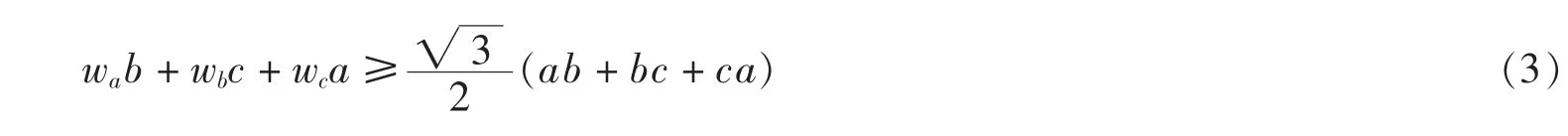
解输入以下命令序列：

>（sgm(wa*b））^2-（sqrt（3）/2*sgm（a*b））^2；#为便于有理化，对不等式两边要同时平方.>auto（%）；

>agl（w1，[aa]）；#由于是锐角三角形，故要带aa参数.

经过数秒运算后，打印出“The inequality holds”，故不等式（3）成立.

解键入以下命令序列：

>sgm（（hb-hc）^2）-k*sgm（（wb-wc）^2）；

>subs（qht，%）；#qht的本质是根据文献［8］建立的公式集.

>factor（subs（x=sqrt（2）/2，solve（%，k）））；则显示：

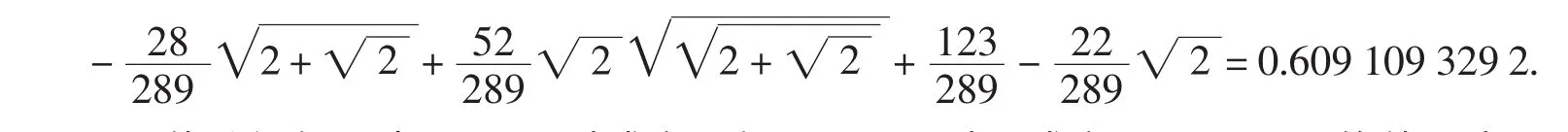
用agl具体验证知，当k=0.6时成立，但k=0.61时不成立（用Bottema软件否定）.虽然这里未能严格证明这个常数就是最佳值，但这个结果仍然让人鼓舞，因为用其他软件是难以得到这种结果的.

例7证明恒等式

证明运行auto命令后发现w1=0，故式（4）是一个恒等式.

例8设k∈R，证明含参不等式

证明不等式（5）化为关于k的一元二次不等式

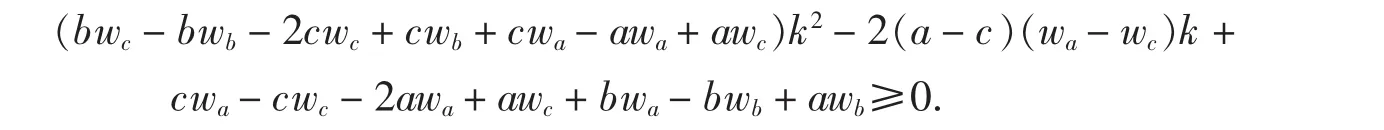
用agl易证二次项系数非负，判别式为-4g，其中g=（-bwa+awa-cwb+bwb+cwc-awc）·（-cwa+awa-awb+bwb+cwc-bwc），用agl易证g≥0成立，由此证得不等式（5）.

例9试对不等式

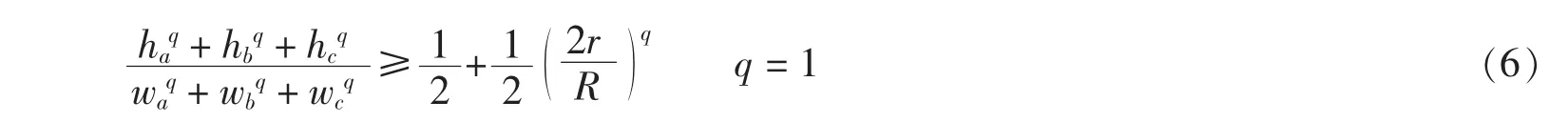
进行判定.

解运行agl（w1）命令后，数秒给出反例多项式.而运行带锐角参数的命令agl（w1，[aa]），很快判定式（6）在锐角三角形中成立.

注如果用Bottema软件寻找不等式（6）的反例，程序运行2 697 s后仍然没有结束迹象.由此可见，agl2009在发现和探讨三角形不等式方面，有一些不可替代的作用.例10在△ABC中，证明不等式

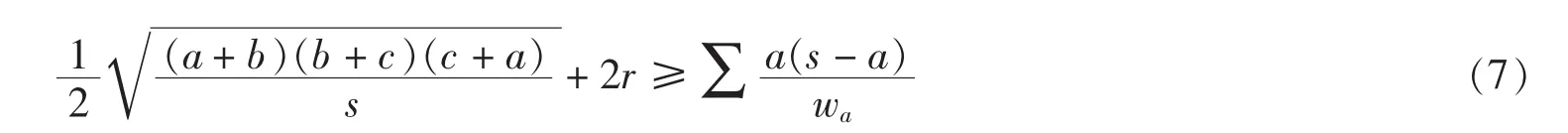
证明不等式（7）两边同时平方，并运行agl（w1）命令后，发现w1中有因式（a-b）2·（b-c）2（c-a）2，故知不等式（7）在等腰三角形时取等号（这类不等式一般非常强），其余证明略.

例11在△ABC中，证明不等式

证明键入agl（w1）命令后，判定没有成功，转入人工处理.经检查知，全局变量o中有一个条件组，且是一个正数组，故证明不等式（8）转化为证明o中正数组的tf部分关于正数m，n，z成立，而这可以用文献中的第二类差分代换程序完成[10].

3 带约束条件差分代换的其他应用

应用带约束条件多项式的差分代换方法，可以将一些根式形式且不易有理化的三角形几何不等式问题转化为条件不等式加以解决.

例12在△ABC中，证明

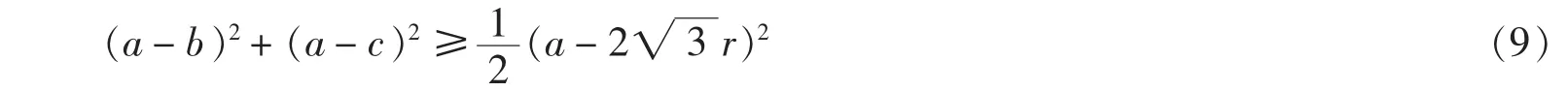
证明不等式（9）等价于如下条件不等式：

对此条件不等式进行代数化，得到一个条件组[f1，f2]（表达式略）.对条件组[f1，f2]进行一次差分代换，得到由3个条件组构成的差分代换集.用agg命令对这3个条件组一一进行检测，结果发现其中有2个是半正定的，另外1个正性不能判定.对这个正性不能判定的条件组继续作差分代换，用agg对得到的条件组进行测试，结果发现全部是正半定的，故不等式（9）成立.

例13在△ABC中,证明

证明不等式（10）可化为条件不等式

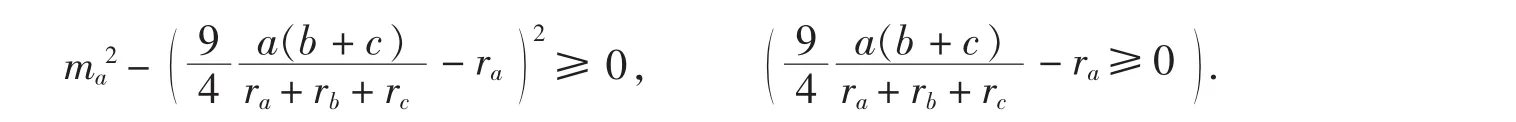
这个条件不等式代数化后可化为一个条件组，对这个条件组作一次差分代换，得到条件组集合（为节约篇幅，这里仅写出了部分表达式）：

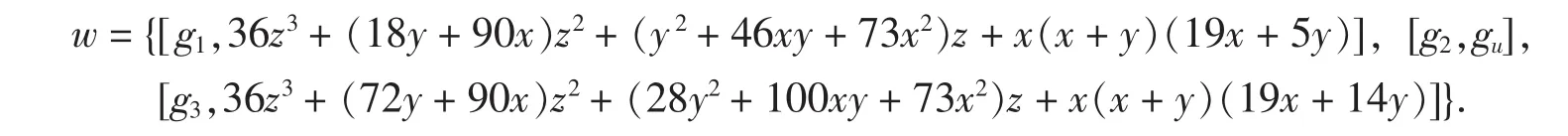
其中，

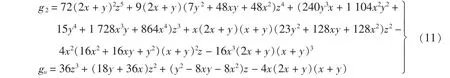
显然w中有2个正数组，其中g3≥0容易用逐次差分代换程序sds[7]判定成立，g1≥0不容易直接判定，但经过倒数代换加速[10]后容易判定.经验证知，剩余的条件组[g2，gu]的正性不能用agl算法判定，故这里我们未完成对不等式（10）的证明.

由例13可以看出，一般条件不等式的证明是十分复杂的.如何对由式（11）决定的条件组[g2，gu]的正性进行判定仍是一个待解决的问题.

4 用agl2009程序发现的优美不等式

截至目前，用agl2009程序已经发现了500多个优美的三角形几何不等式，这些不等式加强或隔离了一些著名的结果，而且其中的许多结果是用其他软件难以判定的.下面摘录若干个形式比较优美的结果（更多结果见http://www.mathlinks.ro/Forum/viewtopic.php?t=315511），同时注明用agl2009程序验证所花费的时间（这些不等式如果用Bottema软件验证，大多数时间超长或不能验证）.

5 结语

本文给出的算法ag，较好地改进了agl算法的不足，据此编写的程序agl2009适用于一大类三角形几何不等式的判定.从使用情况看，由于agl2009程序运行速度提高，形成了人的思维和判定结果同步和互动的局面，这使得一些难度甚大且形式新颖的优美不等式被发现（事实证明，如果不等式证明器的运行时间过长，将会使预热了的思维冷却和迟滞，瞬间产生的灵感火花由于等待而减弱或熄灭，从而使研究效率和质量大打折扣）.虽然如此，agl2009程序尚存在以下不足或问题：一是agl2009给出的反例是条件组，是一种间接反例；二是对于有些不等式，agl2009输出反例的时间过长，而从算法分析来看，反例条件组作为最迟出现的反例，是有改进余地的；三是agl2009的终止性是有缺陷的.另外，由本文可以看出，对于agl算法失效的情形，逐次差分代换不是总能奏效的.如何建立一般条件不等式的判定算法和程序，并向多元进行推广，这些都是十分有价值的研究课题.

最后再提几个有趣的不等式问题：

[1] 刘保乾.三角形几何不等式新探[J].不等式研究通讯，2009，16（4）：440-451.

[2] 刘保乾.不等式研究的几个新结论和新问题[J].嘉应学院学报，2008，26（6）：19-26.

[3]刘保乾.锐角三角形几何不等式的差分代换证法及应用程序[J].佛山科学技术学院学报，2009，27（5）：33-38.

[4] 刘保乾.条件Si类多项式的构造及其他[J].广东教育学院学报，2009，29（5）：8-13.

[5] 杨路，夏壁灿.不等式机器证明与自动发现[M].北京：科学技术出版社，2008：117-142.

[6] 刘保乾.用差分代换研究实数域中多项式的半正定性[J].佛山科学技术学院学报，2008，26（2）：8-11.

[7] 杨路.差分代换与不等式机器证明[J].广州大学学报，2006，5（2）：1-7.

[8] 阙浩涛.否定三角形不等式猜想的一种方法[M]//刘保乾.Bottema，我们看见了什么——三角形几何不等式研究的新理论、新方法和新结果.拉萨：西藏人民出版社，2003：552-556.

[9] 刘保乾.100个优美的三角形不等式新问题[M]//中国初等数学研究（第1辑）.哈尔滨：哈尔滨工业大学出版社，2009：92-95.

[10] 刘保乾.再谈第二类差分代换[J].佛山科学技术学院学报，2009，27（2）：1-6.

Constrained Polynomial Differential Substitution and Applications

LIU Bao-qian
(Information Center，Department of Personnel，Tibet Autonomous Region，Lasa 850000，Tibet，China)

Geometric inequality algorithm is improved and an upgraded version agl2009 isdesigned.Constrainedpolynomial differential substitution isstudied for square root inequalityand several geometric inequalities are found by the agl algorithm.

differential substitution；geometric inequality algorithm；agl algorithm；machine proofing

O 122.3

A

1001-4217（2010）02-0001-10

2009-11-24

刘保乾（1962-），男，陕西凤翔人，计算机本科.研究方向：多项式不等式与机器证明.E-mail：wshr987@163.com