递阶式虚拟结构非完整机器人的编队控制

袁健，张文霞

（1.中国海洋大学信息科学与工程学院，山东青岛266100；2.青岛理工大学琴岛学院机电系，山东青岛266016）

递阶式虚拟结构非完整机器人的编队控制

袁健1，张文霞2

（1.中国海洋大学信息科学与工程学院，山东青岛266100；2.青岛理工大学琴岛学院机电系，山东青岛266016）

提出一种递阶虚拟结构编队控制方法，将机器人编队按空间分布划分为簇，并定义某段时间内该簇（虚拟结构）的参考轨迹，将虚拟结构的运动转化为各机器人的期望轨迹，然后基于反步思想，并通过设计移动机器人误差跟踪系统的Lyapunov函数来设计动态反馈控制器，实现了对参考轨迹的全局渐近跟踪.最后通过对给定直线和圆轨迹的编队跟踪试验，验证了该控制策略的有效性.

移动机器人；编队控制；递阶式虚拟结构；跟踪控制

0 引言

多移动机器人编队控制是多机器人协作的典型问题，是要求各机器人在执行任务时，整个机器人团队建立并保持预先决定的几何形状（如一字形、三角形等），同时又要适应环境变化的一种控制技术.多移动机器人编队控制思想可以广泛应用于陆地自治机器人(AGV)[1-12]、无人驾驶飞行器(UAV)[13-15]、水下自治航行器(AUV)[16-19]以及人造卫星[20-21]等的队形控制问题中，可以完成单个机器人无法实现的控制任务.基于虚拟结构的编队控制方法要求机器人以刚体上相应点的位置和姿态信息作为各自的跟踪目标，这样就可以形成一定的队形[2，4，11，20-21]，与其它编队控制方法相比，其控制思想更容易理解和实现，缺点是采用集中式，无法实现灵活的编队切换，并缺乏对障碍的适应性.文献［4］提出一种分散式编队控制框架，实现了多机器人的编队控制，但其仅针对同类型的机器人，而不能扩展到异类型机器人的编队控制中.文献［11］将协商算法和领航者-跟随者思想应用到机器人的编队控制中，通过即时局部通讯实现了动态的协商控制，但一旦通讯失效则编队失败.文献［20］将主从式、行为式以及虚拟机构式编队思想应用到多深空探测器的编队控制中，并提出一种集中式的协调控制框架，利用多智能体控制思想实现了探测器的编队控制.文献［21］改进了文献［20］的集中式编队框架，并结合虚拟结构思想，实现了航天器的编队控制.编队控制不仅要考虑位置的协调，在实际环境中还需考虑时间上的协调，与路径跟踪方法相比，轨迹跟踪方法更适用于对时间有严格要求的编队控制.文献［22］对非完整移动机器人系统轨迹跟踪控制采取了反步控制方法，对满足一定条件的参考轨迹实现全局指数跟踪，此法要求参考平移速度不趋于零，或参考平移速度趋于零但参考角速度不趋于零.

本文提出一种递阶式虚拟结构编队控制方法，结合leader-follower和virtual structure编队思想，将机器人编队分为若干簇，对簇和簇内机器人的控制采用反步控制来实现具有递阶式虚拟的多机器人编队控制.首先将机器人编队按空间分布划分为簇，并定义某段时间内该簇（虚拟结构）的期望动力学特性，再将虚拟结构的运动转化为各机器人的期望运动（轨迹），然后基于反步思想，通过设计移动机器人误差跟踪系统的Lyapunov函数，来设计动态反馈控制器，通过具有障碍检测能力的机器人（此时为leader）和其它机器人之间的通讯来实现实时的队形切换和反馈，实现了一定性能指标下对参考轨迹的全局渐近跟踪，最后通过对给定直线和圆轨迹的编队跟踪试验，验证了该控制策略的有效性.

1 问题描述

机器人编队需要根据环境信息（障碍）进行相应灵活的队形切换操作，也就是我们要预先指定某种形状的队列以适应周围环境（比如避碰、避障等）.虚拟结构法可以很容易地指定机器人群体的行为，并可以进行队形反馈，机器人之间不涉及复杂的通讯协议，就可以实现各机器人的完全自主运动.一旦选择了某种队形后，机器人之间的相对位置保持不变，即在刚体参考坐标系下坐标不变的情况下，以一定的自由度来改变自己的姿态；多移动机器人以刚体上的相应点作为各自的跟踪目标，就可以形成一定的队形，从而编队控制问题就转化为机器人的轨迹跟踪问题.

1.1 递阶式虚拟结构

本文提出一种递阶式虚拟结构协调框架，用以解决由于通讯范围和带宽约束所导致的整个编队跟踪性能下降的问题.首先将整个编队在空间上分为若干簇，每簇选定一个通讯能力强的机器人作为该簇的领航者，只有领航者之间进行通信，获取期望轨迹后协调每簇的行为.簇间及簇中每个机器人只是按照虚拟结构进行编队控制，这样就可以控制大规模的机器人编队，如图1（a）所示.图1（b）为每簇的控制结构，其中最高层Gi为离散事件监测器，可以演化出一系列的编队模式，其输出为当前编队模式；Fi为编队控制模块，产生并以广播通信的方式协调变量ξi；Ki为机器人个体的局部控制器模块，其输入为机器人的输出向量yi和协调变量ξi，并将ξi转化为要求的机器人位置和指向，然后控制机器人跟踪该要求状态，输出为控制向量ui和性能值zi；最底层的Si代表机器人系统，机器人的输入就是其控制器的输出向量ui，机器人的输出向量yi代表机器人的位姿.为确保跟踪性能，定义各个机器人性能指标：

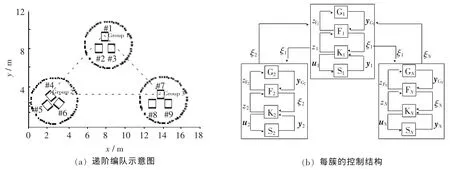
图1 递阶式虚拟结构

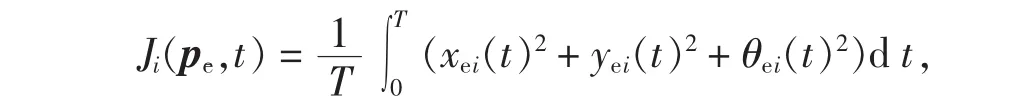
第j簇机器人编队性能指标为：

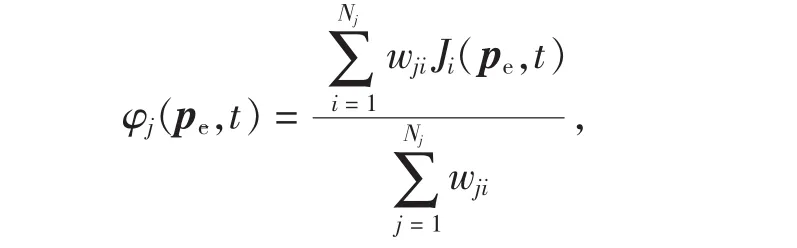
其中Nj为第j簇编队机器人数目，wji为第j簇中第i个机器人的性能权重.则整个编队的性能指标可表示为：

其中M为编队的簇数目，Wj为第j簇权重.根据各机器人控制器模块性能指标Ji，计算各自的性能指标，并向上发送到编队控制模块Fi.Fi计算整个编队性能指标ζ（pe，t），并根据协调变量ξi来判断是否达到期望轨迹而选取性能阈值δ，若不满足期望性能指标则需重新发送协调变量ξi，即ζ（pe，t）＞δ，发送ξi；ζ（pe，t）≤δ，不发送ξi.

1.2 非完整移动机器人轨迹跟踪控制

移动机器人是非完整性系统，非完整性约束表现在车轮只能在垂直于驱动轴的方向滚动而不能产生侧滑.设其具有n个广义坐标（p1，p2，…，pn），则动力学方程可以描述为：

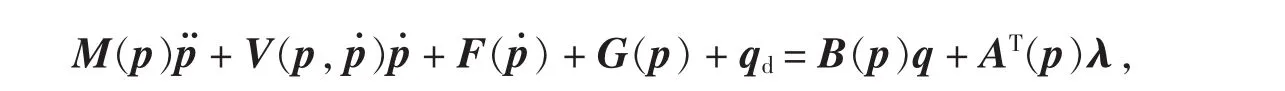
其中M（p）∈Rn×n为对称正定惯性矩阵，V（p，p˙）∈Rn×n为离心力和科里奥利力矩阵，F（p˙）∈Rn表示表面摩擦力向量，G（p）∈Rn为引力向量，qd表示未知有界扰动，B（p）∈Rn×r为输入转换矩阵，q∈Rr为控制量，A（p）∈Rm×n为约束矩阵，λ∈Rm为约束力向量.对于在平面内运动的具有单前轮的移动机器人系统，其运动学方程约束可以表示为A（p）Tp˙=0，其中p=[x，y，θ]T表示机器人的运动状态，q=[υ，ω]T表示机器人方程的控制输入.（x，y）为机器人在惯性坐标系下的位置坐标，θ=arctan（y˙（t）/x˙（t））为驶向角，υ，ω分别为机器人的线速度和角速度，约束方程为y˙cosθ-x˙sinθ=0，约束矩阵可写为A（p）=[sinθ，-cosθ，0]T，所以A（p）Tp˙=0，又由矩阵为约束矩阵A（p）的零空间，即A（p）TS（p）=0.因此p˙=S（p）q，为其运动学模型.

在移动机器人工作平面内建立两个坐标系，分别为惯性坐标系x-o-y和机器人本体坐标系x′-o′-y′.如图2所示，机器人状态由其两驱动轮的中点在惯性坐标系下的位置及驶向角来表示.

机器人运动学方程为：

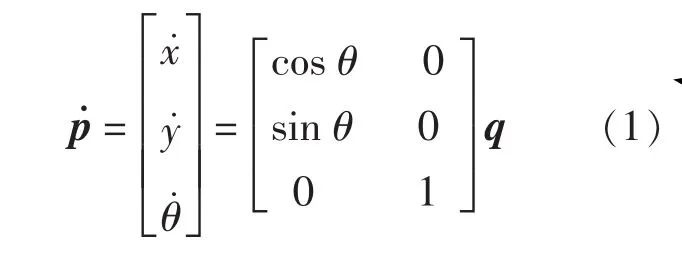
并具有速度非完整约束x˙sin θ=y˙cos θ.

轨迹跟踪问题就是要找到υ和ω的

控制律，使机器人跟踪参考轨迹[xd，yd，θd]T和参考速度输入υd和ωd，如图2所示.

在机器人本体坐标系下的位姿误差定义为[22]：

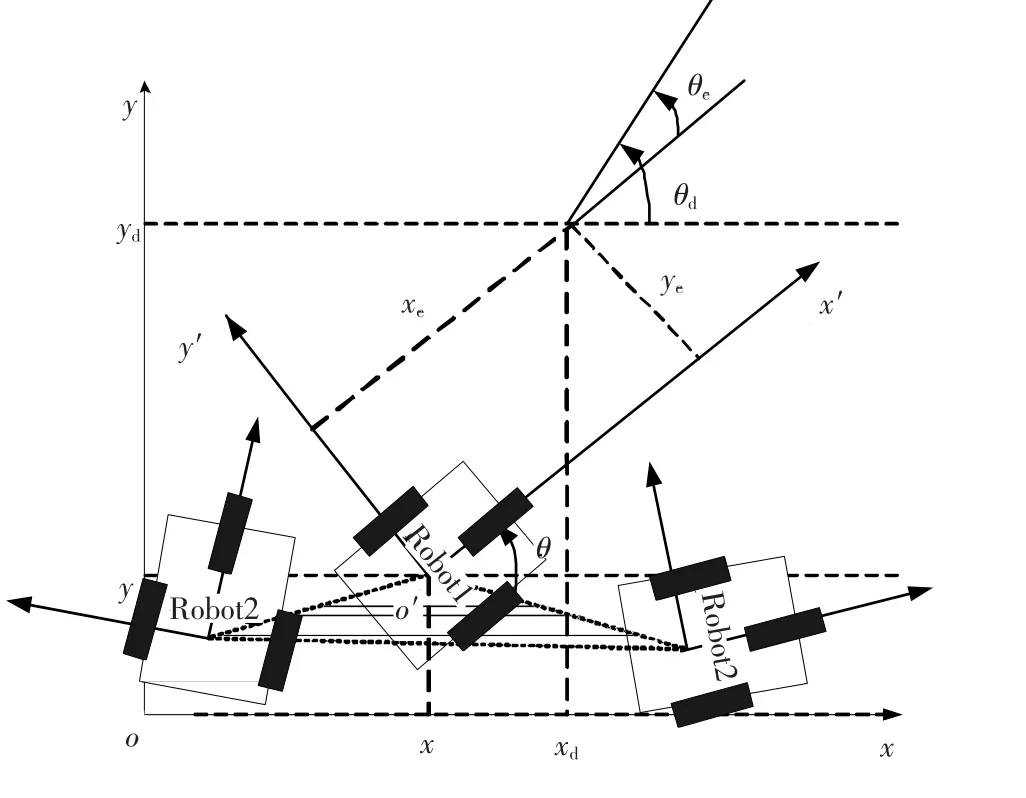
图2 移动机器人的位姿及误差

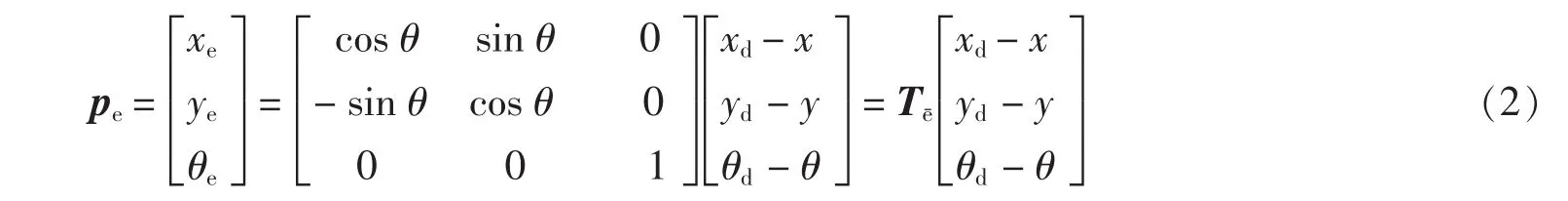
其中Te为从惯性坐标系到机器人本体坐标系的转换矩阵.

对式（2）求时间导数，所以误差的动力学方程可以写为：

可得：

其中υ，ω分别可以表示为：υ=υ（xe，ye，θe，υd，ωd），ω=ω（xe，ye，θe，υd，ωd）.移动机器人运动学模型的全局轨迹跟踪问题，即通过控制输入q，使得对任意初始误差[xe（0），ye（0），θe（0）]T，方程（3）的闭环轨迹和控制υ，ω一致有界且.跟踪控制系统框如图3所示，参考轨迹pd是参考输入υ通过参考系统得到的系统输出，其中，NC为非线性控制器，Σ1为受控机器人系统（1），Σd为参考系统的运动学方程：

图3 跟踪控制框

2 编队控制器设计

针对非完整机器人编队形成问题，上节提出了一种递阶式虚拟结构的编队形成策略，并将编队问题转化为机器人的轨迹跟踪问题，本节将讨论轨迹跟踪控制器的设计问题.

定理1假设υd和ωd在[0，∞）上一致连续并有界（υd和ωd不同时收敛到0），可以设计控制律υ和ω，使得系统（3）全局渐近稳定，即，其中，

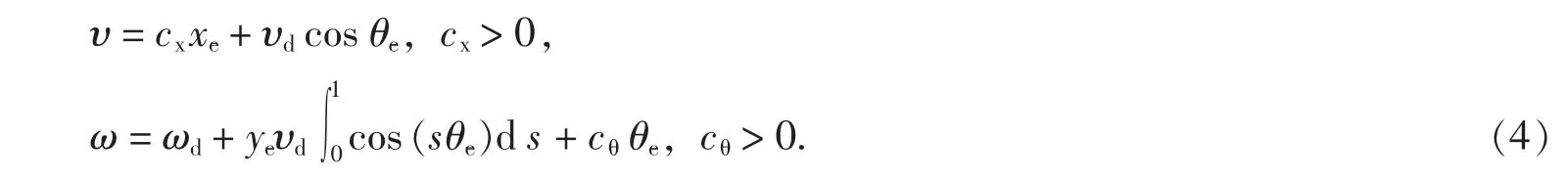
证明若令xe=c1ωye，θe=0，则可使式（3）中的ye→0.

其中α=ωye+υdcos θe-c1ye-c1ω（-ωxe+υdsin θe）.

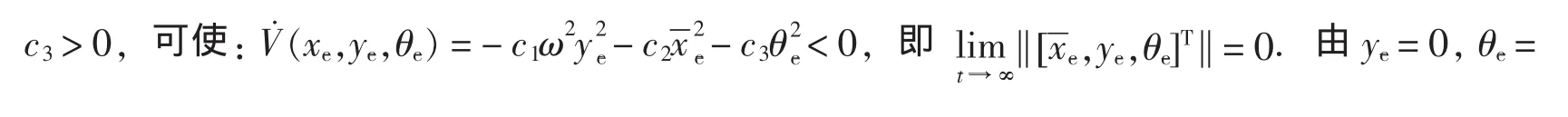
3 仿真算例

例1横向编队并实现直线轨迹跟踪控制问题.设3个机器人Robot1、Robot2、Robot3的初始位置状态分别为：

Robot1、Robot2、Robot3预先指定的跟踪轨迹的位置初值分别为：

三者间保持0.2 m的横向距离，直线轨迹初始斜率为k=1，当t=400 s时斜率变为0.选取ωd=0 rad/s，υd=0.2 m/s，c1=3，c2=3，c3=10，w11=w12=w13=1，仿真步长τ＝100 ms，仿真时间T=1 000 s.当t=0 s，100 s，300 s，500 s，600 s，1 001 s时的位姿如图4所示.各个机器人的性能指标Ji（pe，t）、总性能指标随时间变化而变化的曲线如图5所示.取性能阈值δ＝1.0，从表1中可以看出，t=100 s时满足性能要求；t=400 s轨迹发生改变，导致性能指标变大，但又很快收敛.

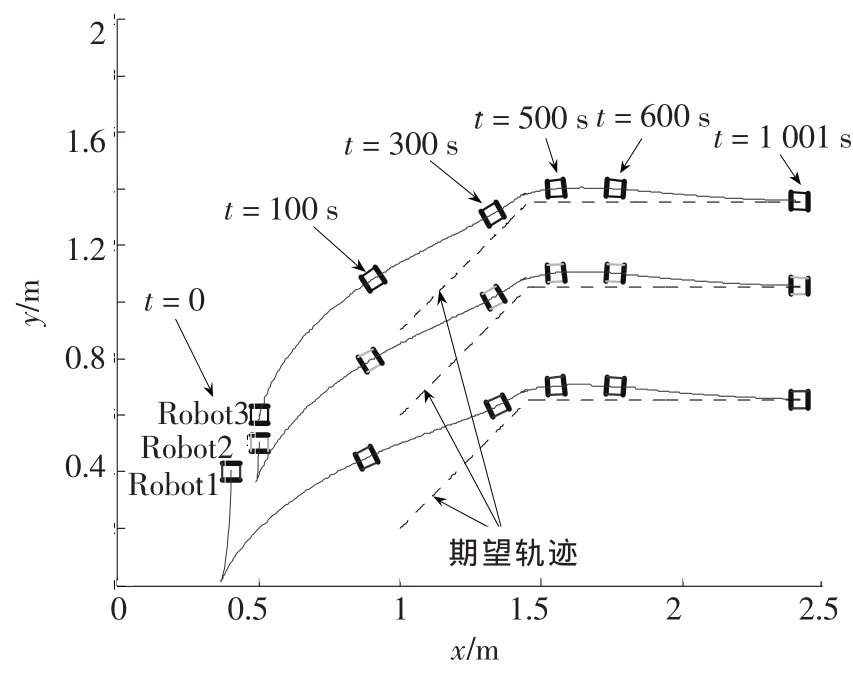
图4 三机器人横向编队

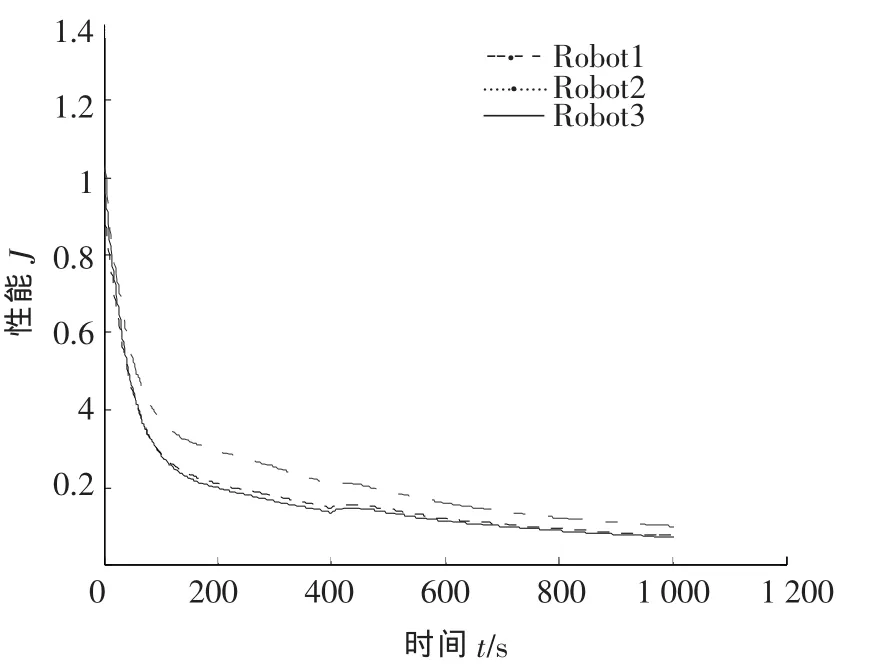
图5 各机器人性能指标

表1 横向编队跟踪误差指标

例2三角形编队并实现圆形轨迹跟踪控制问题.3个机器人Robot1、Robot2、Robot3的初始位置状态分别为：

Robot1、Robot2、Robot3预先指定的跟踪轨迹的位置初值为：

选取ωd=0.05 rad/s，υd=0.05 m/s，w11=w12=w13=1，仿真步长τ＝100 ms.c1=1，c2=122，c3=19，初始轨迹圆半径为r1=1.8 m，在t=400 s时，期望轨迹发生改变，圆半径为r2=2 m，仿真时间T=1 000 s.图6中分别标注了3个机器人在t=0 s，25 s，300 s，400 s，500 s，600 s，1 001 s时的位姿.性能指标Ji（pe，t）、总性能指标ζ（pe，t）＝随时间变化而变化的曲线如图7所示.取性能阈值δ＝1.0，从表2中可以看出，t=25 s时满足性能要求；t=400 s轨迹发生改变，导致性能指标变大，但又很快收敛.

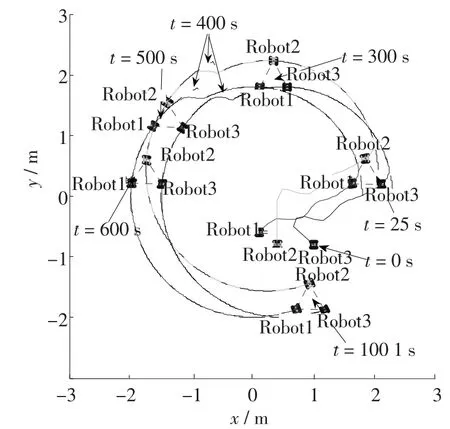
图6 三角形编队实现圆轨迹跟踪

图7 各机器人性能指标

表2 三角编队跟踪误差指标

4 结语

本文研究了跟踪轨迹为直线和圆两种情形的多移动机器人编队形成和控制问题，通过构造Lyapunov函数使其导数负定来构造反步控制器，并基于分布式虚拟结构方法实现了多机器人的平行编队和三角编队，使其能够在无障碍情况下保持队形并快速收敛到期望轨迹.通过仿真验证了该方法的有效性.

[1] Wang P K C.Navigation strategies for multiple autonomous mobile robot s moving in formation [J].Journal of Robotic Systems，1991，8（2）：177-195.

[2] Lewis M A，Tan K H.High precision format ion cont rol of mobilerobot s using virt ual structure approach[J].Autonomous Robots，1997（4）：387-403.

[3] Balch T，Arkin R C.Behavior-based formation control for multi-robot teams[J].IEEE Transactions on Roboti cs and Automation，1998（14）：926-939.

[4] Lawton A R，Young B J，Be ard R W.A decent ralized approach to eleme ntary format ion maneuvers[C]//IEEE Internat ional Conference on Robot ics and Automat ion.San Francisco：IEEE Press，2000（3）：2728-2 733.

[5] Leonard N E，Fiore lli E.Virt ual leader，artif icial pote ntials and coordinate d cont rol of groups[C]//IEEE Conferenceon Decision and Cont rol.Orlando：IEEE Press，2001（3）：2 968-2 973.

[6] Dunba W B，Murray R M.Model predictive control of coordinate d multi-vehicle formations[C]//IEEE Conference on Decision and Cont rol.Las Ve gas：IEEE Press，2002（4）：4 631-4 636.

[7] Desai J P.A graph theoretic approach f or modeling mobile robotteam formations [J].Journal of Robotic Systems，2002，19（11）：511-525.

[8] Lawton J R，Beard R W，Young B J.A decentralized approach to formation maneuvers[J].IEEE Transactions on Robotics and Automation，2003，19（6）：933-941.

[9] Do K D.Formation tracking control of unicycle-type mobile robots with limited sensing ranges[J].IEEE Transactions on Control Systems Technology，2008，16（3）：527-538.

[10] De La Cruz C,Carelli R.Dynamic model based formation control and obstacle avoidance of multirobot systems[J].Robotica,2008,26（3）：345-356.

[11] RenW,Sorensen N.Distributed coordination architecture for multi-robot formation control[J].Robotics and Autonomous Systems,2008,56（4）：324-333.

[12] Dong Wenjie，Farrell J A.Decentralized cooperative control of multiple nonholonomic dynamic systems with uncertainty[J].Automatica，2009（45）：706-710.

[13] Ryan A，Zennaro M，Howell A，et al.An overview of emerging results in cooperative UAV control[C]//IEEE Conference on Decision and Control.Paradise Island：IEEE Press，2004（1）：602-607.

[14] Galzi D,Shtessel Y.UAV Formations control using high order sliding modes[C]//American Control Conference.Minnesota：IEEE Press，2006：4 249-4 255.

[15] Seungkeun K，Youdan K.Three dimensional optimum controllers for multiple UAV formation flight using behavior-based decentralized approach[C]//International Conference on Control.Seoul：IEEE Press，2007：1 387-1 392.

[16]Tangirala S，Kumar R，Bhattacharyya S，et al.Hybrid-model based hierarchical mission control architecture f or aut onomous underwat er vehicles[C]//American Cont rol Conference.Oregan：IEEE Press，2005（1）：668-673.

[17] Okamoto A，Edwards D B，Anderson M J.Robustcont rol of a plat oon of underwat er autonomous vehicles [J].Sea Technology，2005，46（12）：10-13.

[18] Yang E F，Gu D B.Nonlinear formation-keeping and mooring cont rol of mult iple autonomous unde rwater vehicles[J].IEEE/ASME Transact ions on Mechatronics，2007,2（2）：164-178.

[19] Kalantar S，Zimmer U R.Distributed shape cont rol of homogeneous swarms of autonomous underwat er vehicles[ J].Autonomous Robots，2007，22（1）：37-53.

[20] Beard R W，Lawton J，Hadacgh F Y.A coordination architecture for spacecraft format ion control[J].IEEE Transactions on Cont rol Systems Technology,2001,9（6）：777-790.

[21] Ren W,Beard R W.Decentralized scheme for spacecraft formation flying via the virtual structure approach[J].Journal of Guidance，Control and Dynamics，2004，27（1）：73-82.

[22] Tiang Z P，Nijmeujer H.Tracking control of mobile robot s：A case st udy in backst epping [J].Automatica，1997，33（7）：1 393-1 399.

Formation Control for Mobile Nonholonomic Multi-Robots with Hierarchical Virtual Structure

YUAN Jian1，ZHANG Wen-xia2
（1.College of Information Science&Engineering,Ocean University of China,Qingdao 266100,Shandong,China;2.Mechanical&Electrical Engineering Department,Qindao College,Qingdao 266016,Shandong,China）

s：Theformationcontrol problem ofmobilenonholonomicmulti-robots is investigated.A formation control structure with hierarchical Virtual Structure is proposed.The mobile robots are divided into some clusters according to their distributions in space and motion trajectory of every cluster（virtual structure）.The motion of virtual structure is transformed to desired trajectory of every robot.A Lyapunov function of the error tracking system is constructed based on the backstepping method to design dynamic feedback tracking controller.The tracking controller can make the trajectory of every mobile robot globally and asymptotically track a desired trajectory.Finally，formation simulations considering line and circle shape are carried out and the numerical simulation results show the effectiveness of the proposed control scheme.

nonholonomic；mobile robot；formation control；hierarchical virtual structure；trackingcontrol

TP 273

A

1001-4217（2010）02-0042-09

2009-11-18

袁健（1980-），男，山东荣成人，博士.研究方向：计算机控制及仿真技术.E-mail：jyuangjian@ouc.edu.cn