矩阵多项式的综合除法及其应用

谢泽嘉

（华南师范大学数学科学学院，广东广州510631）

矩阵多项式的综合除法及其应用

谢泽嘉

（华南师范大学数学科学学院，广东广州510631）

给出矩阵多项式的综合除法，利用微分代数的观点，将其应用于一类常系数偏微分方程化为无穷维Hamilton系统的问题中.再结合标准型算法，将其应用于构造一类偏微分方程组通解的问题中.

无穷维Hamilton系统；带余除法；综合除法；矩阵多项式；偏微分方程组通解

0 引言

求微分方程（组）的等价无穷维Hamilton系统是分析力学的反问题，是经典力学的主要问题之一.阿拉坦仓[1]提出了矩阵多元多项式带余除法的理论，并将其应用于解决常系数偏微分方程（组）的无穷维Hamilton系统的反问题.陆斌及张鸿庆[2]将矩阵多元多项式带余除法与标准型算法相结合，获得构造一类偏微分方程组通解的新方法.关于矩阵多元多项式带余除法的计算，侯国林和阿拉坦仓[3]利用Mathematica系统将文献［1］中的结果编制成矩阵多元多项式带余除法软件包，用于求商式与余式.本文将类比多项式的综合除法，给出矩阵多项式的综合除法，以解决常系数偏微分方程（组）的无穷维Hamilton系统的反问题和构造偏微分方程组通解中所涉及的矩阵多项式的带余除法问题.

1 矩阵多项式的带余除法

若m×n矩阵（m、n均为正整数）A（s）的每个元素都是关于s的多项式，则称A（s）为m×n阶矩阵多项式.

若矩阵多项式的次数∂[A（s）]=k（其中k为正整数），则A（s）可表示为A（s）＝A0sk＋A1sk－1＋…＋Ak，其中A0，A1，…，Ak称为A（s）按总幂次展开的系数矩阵.其它关于A（s）的按行（列）幂次展开及按指定行（列）幂次展开的情况可参考相关文献[4].

文献给出了当除式为方阵时的带余除法[5]，本文将带余除法推广到除式为矩形阵的情况，证明从略.以下r、l、m均为正整数，Rr×l[s]表示r×l的实系数矩阵多项式环.

左除设A（s）∈Rr×l[s]为行正则，B（s）∈Rr×m[s]，∂[B（s）]≥∂[A（s）]，则存在唯一的商式Q（s）∈Rl×m[s]和余式R（s）∈Rr×m[s]，使得：

其中，∂riA（s）表示A（s）第i行的次数.

右除设A（s）∈Rl×r[s]为列正则，B（s）∈Rm×r[s]，∂[B（s）]≥∂[A（s）]，则存在唯一的商式（s）∈Rm×l[s]和余式（s）∈Rm×r[s]，使得：

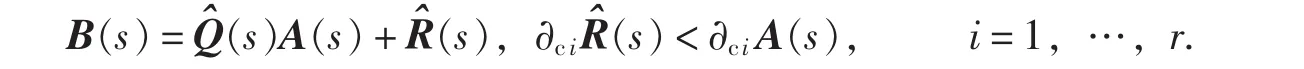
其中，∂ciA（s）表示A（s）第i列的次数.

对于上面矩阵多项式的带余除法，在具体求商与余时，左除时A（s）必须是按行幂次展开，并要求展开后的首项系数阵行满秩，B（s）则必须是按与A（s）行幂次相同的指定行幂次展开；右除时A（s）必须是按列幂次展开，并要求展开后的首项系数阵列满秩，B（s）则必须是按与A（s）列幂次相同的指定列幂次展开.另外，若A（s）按总幂次展开时的首项系数阵为行（列）满秩矩阵，则同样有类似于上面的关于按总幂次展开的左除（右除），并且被除式也是按总幂次展开.

2 矩阵多项式的综合除法

矩阵多项式也有类似于多项式的综合除法，当被除式与除式行数相同时可以进行左除，列数相同时可以进行右除.下面给出除式和被除式按总幂次展开的情况.

对于A（s）∈Rr×l[s]左除B（s）∈Rr×m[s]的情况（∂[A（s）]=k，∂[B（s）]=h，h＞k，h、k均为正整数），由矩阵多项式的带余除法，可令B（s）=A（s）Q（s）+R（s），其中，Q（s）=Q0sh-k+

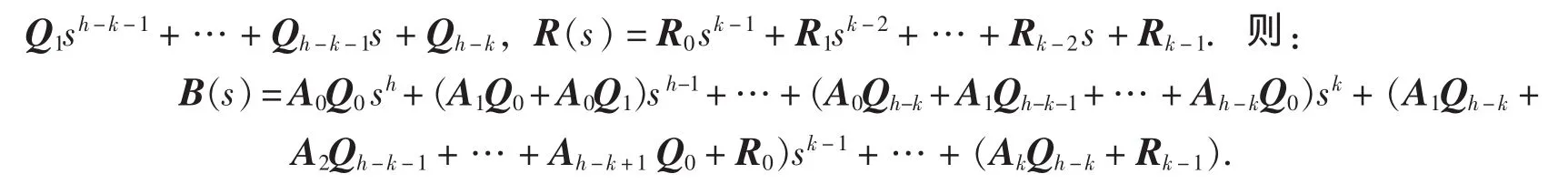
由矩阵多项式恒等可得：

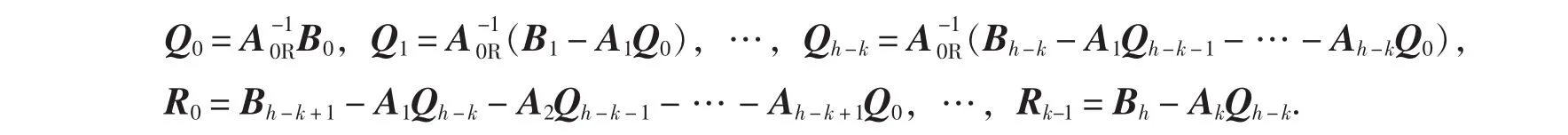
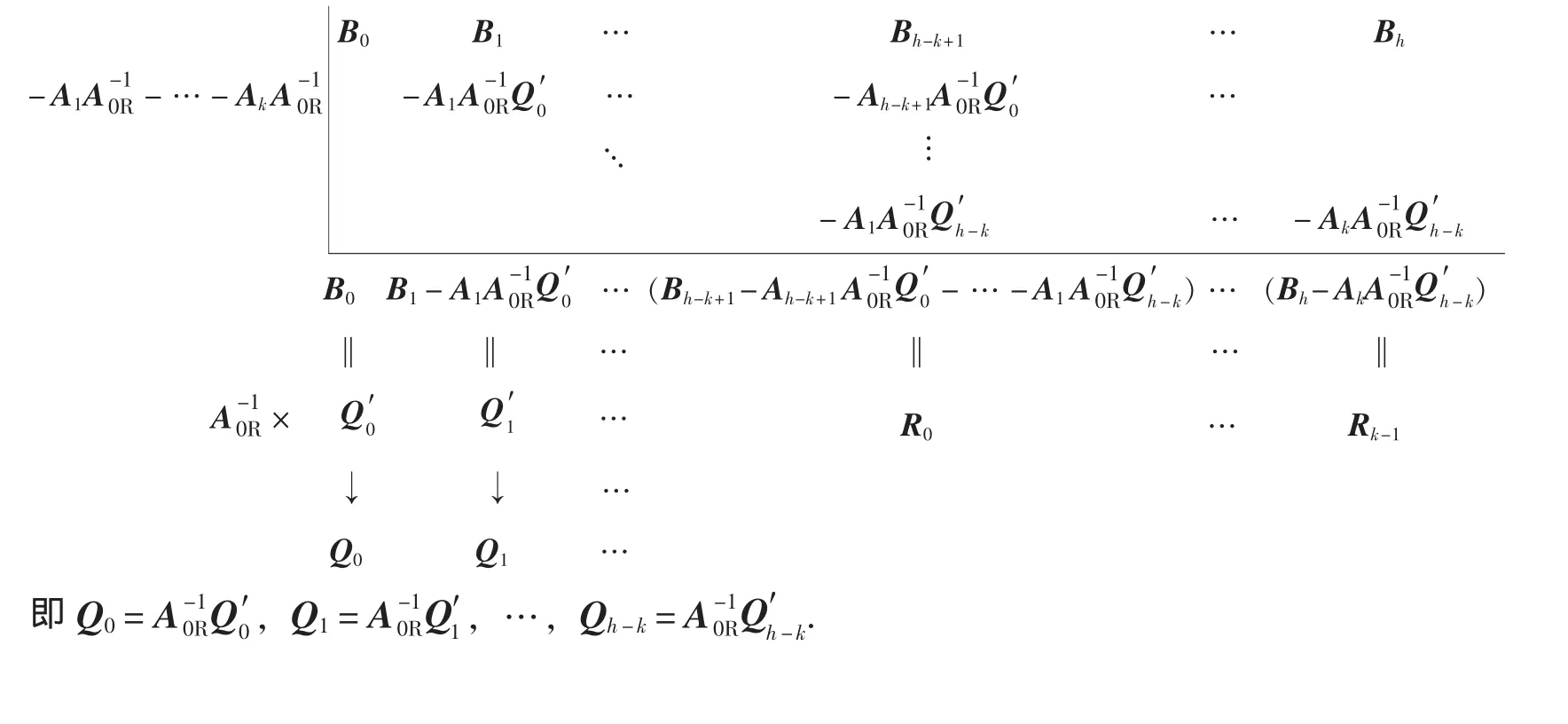
对于A（s）∈Rl×r[s]右除B（s）∈Rm×r[s]的情况（∂[A（s）]=k，∂[B（s）]=h，h＞k，h、k均为正整数），同理，由矩阵多项式的带余除法，可令B（s）=Q^（s）A（s）+R^（s），其中，

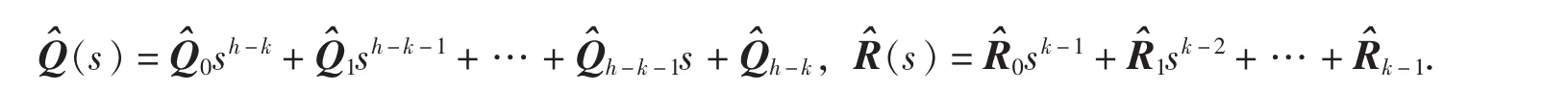
同理可得：

注：上面作左除和右除时，矩阵多项式的综合除法的表示形式是不同的.对于左除，形式是“⌉”，而对于右除，形式则是“」”.这样表示的原因是矩阵的乘法一般是不可交换的.

综合除法左除按行幂次展开的情况与右除按列幂次展开的情况，分别与左除和右除按总幂次展开的情况类似.

另外，在利用矩阵多项式的综合除法求左（右）除的商式和余式时，首先判断除式按总幂次展开的首项系数阵是否行（列）满秩，若是则进行综合除法，否则再判断除式按行（列）幂次展开的首项系数阵是否行（列）满秩，是则进行综合除法，否则不能.

3 矩阵多项式综合除法的应用

3.1 在无穷维Hamilton系统中的应用

关于无穷维Hamilton系统的相关概念可参考阿拉坦仓教授的文献[6].

解该偏微分方程可写为多元多项式：

其中关于x的次数为2.故无穷维Hamilton系统的矩阵多元多项式为

后面的步骤与文献［6］例2.1一样.

3.2 在构造偏微分方程组通解中的应用

文献［2］给出了一种用机械化的方法构造一类微分方程组的通解.首先对微分方程组Au＝0在不同序下求出其标准型，从每个标准型中取只含某个未知函数的适当的方程作为目标方程Dυ＝0（其中，u，υ为函数列向量再利用矩阵多项式的综合除法求原方程组Au＝0去除目标方程Dυ＝0所得的商与余，这时，一般情况下余式R＝0，从而得到变换公式和通解.关于标准型的概念及标准型算法可参考文献［2］.下面以文献［2］中的一个例子来说明矩阵多项式综合除法的应用.

例2求方程组

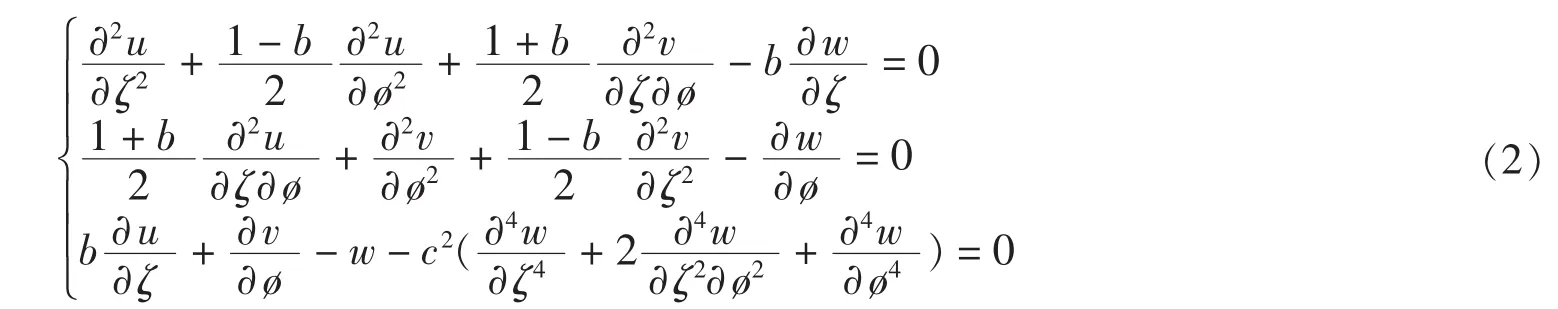
的通解（这里b、c是常数）.

解由文献［2］可知目标方程可选为：

上述方程两边同时乘以c2，并改写成多元多项式的形式为：

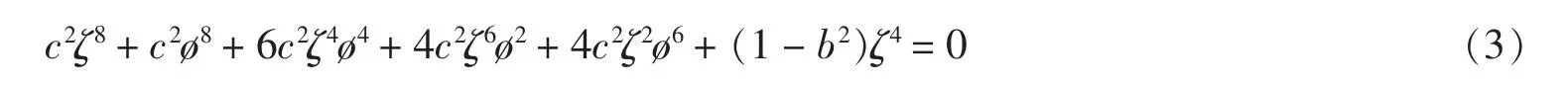
由于原方程组（2）有u、v、w3个未知函数，且关于这3个未知函数的“系数矩阵”为（偏微分算子均写为多元多项式，并以变量ζ为主元，由于按总幂次展开时首项系数矩阵非行满秩，故按行幂次展开）:

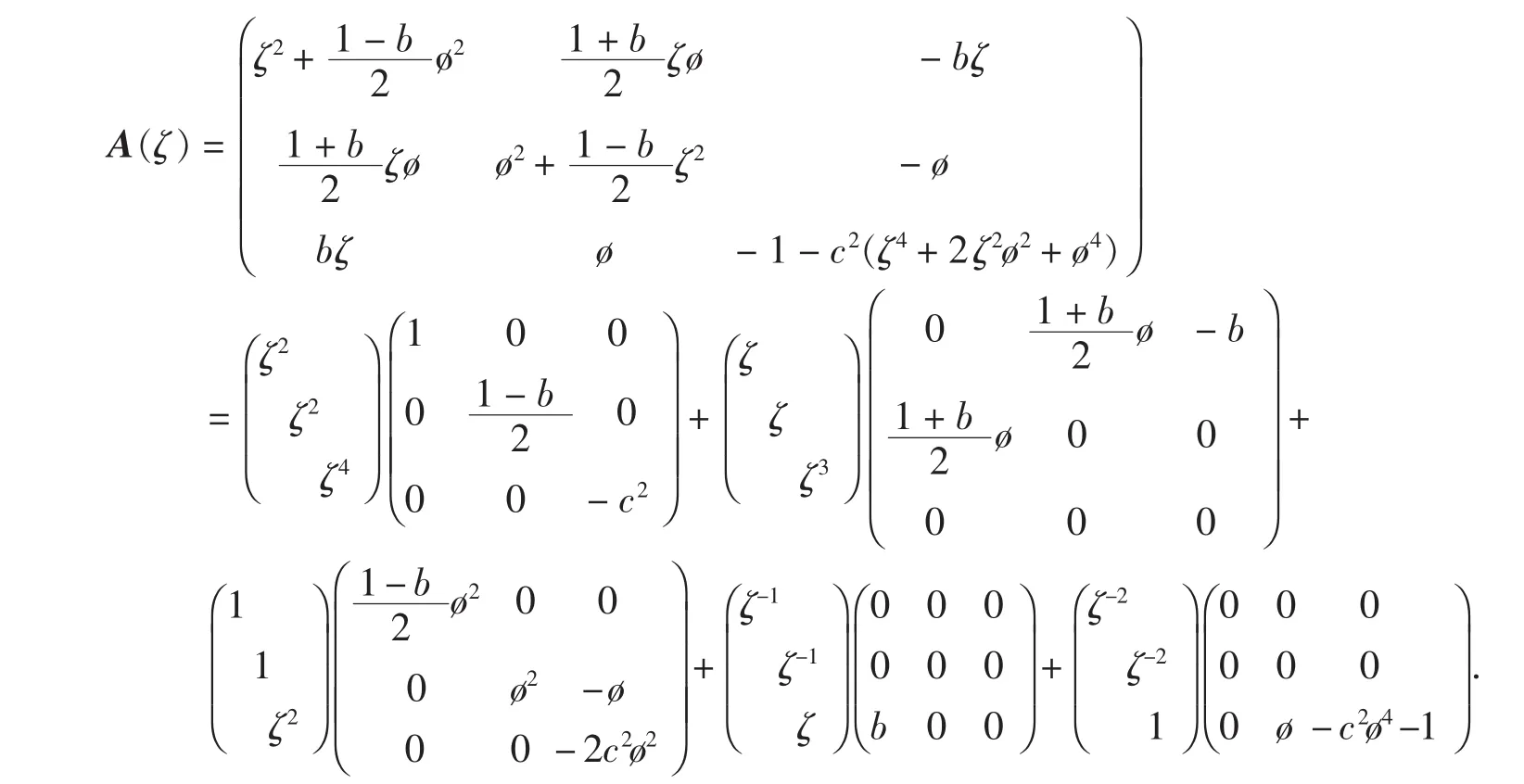
将主元为ζ的多元多项式（3）化为三阶向量的形式，并按与“系数矩阵”相同的指定行幂次展开，得：

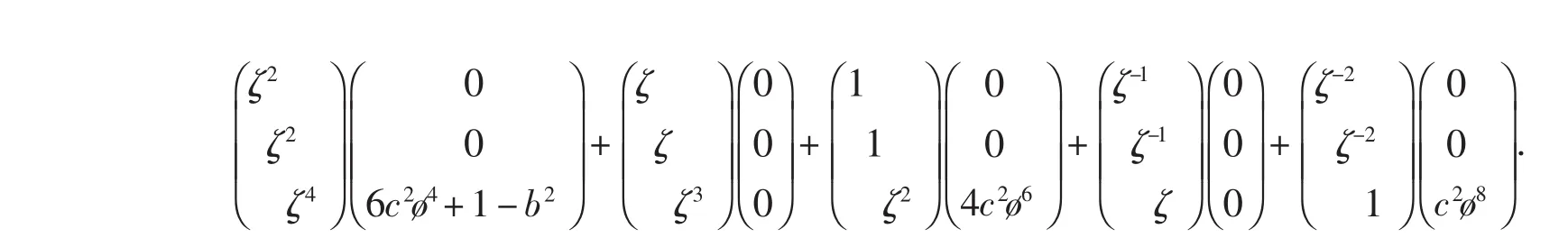
可知余式R（ζ）=O3×1（其中O3×1表示3×1的零矩阵），商式

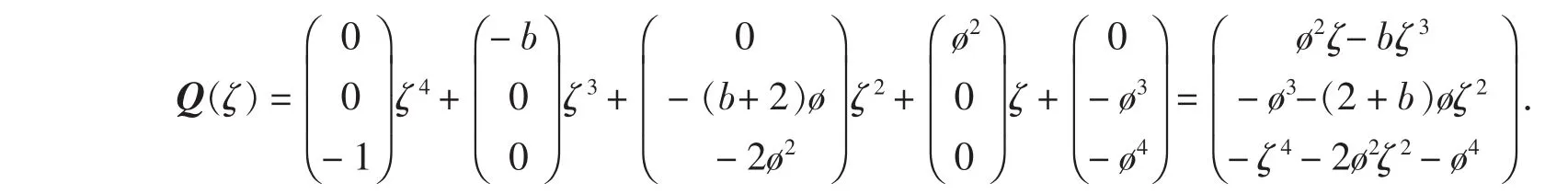
因此，有如下的分解式成立：

的通解[2].

本文类比多项式的综合除法，给出矩阵多项式的综合除法.该综合除法除了解决矩阵多项式除法的求商式与余式问题，在实际应用中也有重要作用，如本文的例1和例2.不足之处就是碍于综合除法的“形式”，需要人工计算，比较繁复.但从原理来看，该算法具有一般性，机械性，从而也可以在计算机上实现，而且有更好的计算能力.矩阵多项式的综合除法可进一步推广，如文献[7]给出的升幂与降幂综合除法.有关矩阵多项式综合除法的更多推广和应用仍有待于进一步的研究.

致谢：对汪立民教授的帮助谨致感谢.

[1] 阿拉坦仓，张鸿庆，钟万勰.矩阵多元多项式的带余除法及其应用[J].应用数学和力学，2000，21（7）：661-667.

[2] 陆斌，张鸿庆.构造一类偏微分方程组通解的机械化方法及力学方程的自动推理[J].山东科技大学学报（自然科学版），2002，21（1）：18-24.

[3] 侯国林，阿拉坦仓.二元矩阵多项式的首一分解[J].内蒙古大学学报（自然科学版），2004，35（5）：490-494.

[4] 韩京清，许可康.线性控制系统理论——构造性方法[M].北京：科学出版社，2001：13-15.

[5] 罗宗虔.控制系统CAD常用算法基础[M].武汉：华中理工大学出版社，1991：216-219.

[6] 阿拉坦仓.无穷维Hamilton系统的反问题[J].内蒙古大学学报（自然科学版），1998，29（5）：619-623.

[7] 谢泽嘉.升幂与降幂综合除法在线性控制系统中的应用[J].韶关学院学报，2009，30（9）：8-13.

Synthetic Division of Matrix Polynomial and Its Application

XIE Ze-jia
（School of Mathematical Sciences,South China Normal University,Guangzhou 510631,Guangdong,China）

The synthetic division of matrix polynomial is given and will，on the basis of differential algebra,be applied in the problem solutions pertaining to the transformation fromconstantcoefficientpartialdifferentialequotiontotheinfinitedimensional Hamiltonian system.In addition，combined with thestandard formalgorithm，the synthetic division of matrix polynomial also finds application in constructing general solutions for a class of partial differential equations.

infinite dimensional Hamiltonian system；division with remainder；synthetic division；matrix polynomial；general solutions of partial differential equations

O 175.25

A

1001-4217（2010）02-0016-08

2009-12-01

谢泽嘉（1987-），男，广东揭阳人，本科.研究方向：数学与应用数学.E-mail：1051863526＠qq.com