基于半结构性决策理论的投资方案模糊优选方法

李建平，杨海鹰，邱念芳

（1.河南工业大学 土建学院，郑州 450052；2.鹤壁市深鹤污水处理有限公司，河南 鹤壁 458030）

1 基本理论

对投资方案进行考察时，根据工程的需要，要考虑项目的多个属性。而不同的属性可以由不同的方式进行刻画，有些是定量的，有些是定性的。对于不同类型的指标，其处理方法也是不同的。关于相对隶属度的基本理论如下：

所谓相对优属度，是指标对优的相对隶属度。对于定性的指标，求其相对优属度的方法如下：

设决策系统由n个投资方案构成方案集：

式中，dj表示第j个投资方案，每个方案有m1个定性指标，对于定性指标i而言，可定义方案集D关于定性指标i对优越性作二元比较的定性排序标度矩阵iE。

定义2 方案集D中的元素dk与dl，就定性指标i作二元比较，若:（1）dk比 dl优越，记标度iekl=1，ielk=0；（2）dk比 dl同样优越，记iekl=0.5，ieik=0.5；（3）dl比 dk优越，记标度iekl=0，ielk=1(k=1,2,…,n；l=1,2,…,n)。 则矩阵：

称为方案集D关于定性指标i对优越性作二元比较的定性排序标度矩阵。

对于矩阵iE，如果对比排序没有矛盾，则称该矩阵是排序一致性的。有如下定理：

定理1 方案集D关于定性目标I对优越性作二元比较的定性排序标度矩阵iE为排序一致性（或传递性）标度矩阵的必要且充分条件为：（1）若iehk＞iehl，有iekl=0；（2）若iehk＜iehl，有iekl=1；（3）iehk=iehl=0.5 若，有iekl=0.5（h=1,2,…,n）。

定理1的证明见文献[4]，根据定性排序一致性标度矩阵iE各行元素之和由大到小的排列，可给出投资方案集D关于定性指标i在满足排序一致性（传递性）条件下对于优越性的定性排序。根据已得的优越性排序一致性标度矩阵iE，将各投资方案按照上述方法从优到劣的顺序进行排序。有如下定义：

定义3 设方案集（就定性指标而言）在优越性排序后作二元比较，若二元比较矩阵：

满足条件：

则iA称为方案集（就指标i而言）对优越性的有序二元比较矩阵。

公式（5）中，iajk表示就指标 i而言，将投资方案 dj与 dk的优越性作二元比较时，方案dj对dk的优越性定量标度。决策方案序号按照矩阵iE各行和数由大到小的次序排列。

就指标 i而言，若方案 dj比 dk优越，则iajk＞iakj，反之亦然。若方案di和dk同等，则iajk=iakj=0.5。

设方案集D=(d1,d2,…dn)就定性指标而言的相对优属度向量为：(1ri1,1r12,…1rin)。因为投资决策方案的序号是按照优越性进行的有序排列，有1ri1＞1ri2＞…＞1rin，可以证明：

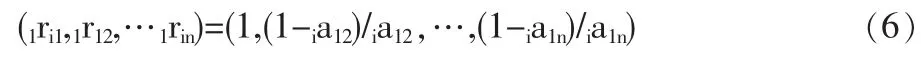
方案dj就定性指标i而言的相对优属度可由下式计算：

式中，ia1j为方案集（就指标i而言）对优越性的有序二元比较矩阵iA 中第 1 行第 j个元素，0.5≤ia1j≤1，j=1,2,…,n。

假设决策系统有m1个定性指标，可以得到如下矩阵：

式中，1rij为方案dj根据定性指标的相对优属度，i=1,2,…,m1，j=1,2,…,n。

假设决策系统中有m2个定量指标，有下述矩阵：

式中，xij表示方案dj关于第i个指标的特征值。

对于收益型指标，可由下式计算方案dj就第i个定量指标而言的相对优属度：

对于成本型指标，可由下式计算方案dj就第i个定量指标而言的相对优属度：

可以得到如下关于定量指标的相对优属度矩阵

式中，2rij表示方案dj根据定性指标i的相对优属度。

可以证明，由公式（10）和公式（11）得到的定量指标相对优属度与由公式（7）得到的定性指标相对优属度具有统一的计算标准[8]。所以可以将R1和R2合并为一个矩阵，设m=m1+m2，则该矩阵为m行，n列，有决策系统的相对优属度矩阵：

2 模糊优选模型

2.1 求指标权重

指标的权重反映了决策者对不同指标的偏好，确定权重的方法与求关于定性指标相对优属度的方法类似，具体可见文献[5]。

2.2 多级模糊优选模型

决策方案的优劣程度依据m个指标特征值，按从优到劣的c个级别进行识别，可以规定最优级（1级）的相对优属度为1，最劣级（级）的相对优属度为0。可以认为由1级到级的相对优属度从1到0线性递减，则相邻级别的相对优属度递减值为：

对于任一指标，第h（h=1,2,…,c）级的相对优属度标准值sh为：

将决策系统的相对优属度矩阵R中的第j列向量的第i个元素与各个级别的相对优属度标准值相比较得到该元素分别属于相邻级别区间[aij,bij]，可求得投资方案dj的级别上限值bj和级别下限值aj：

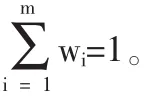
可求得方案dj对级别h的相对隶属度uhj[5]：

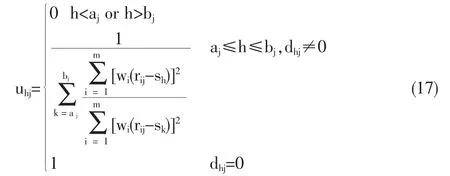
根据上式，可求得投资方案集属于各个级别的相对隶属度矩阵：

求得级别特征值的向量式：

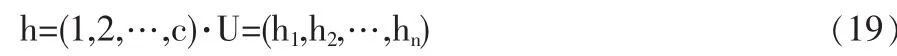
3 实证分析

某水电投资项目，以水力发电为主，对不同的投资方案进行模糊优选。

3.1 项目评价的指标体系及备选方案

考虑的评价指标有：财务净现值（a1）、动态投资回收期（a2）、装机容量（a3）、年发电量（a4）、每千瓦投资额（a5）、移民数量（a6）、淹没耕地面积（a7）、环境保护（a8）、施工容易度（a9）共 9项指标，其中，环境保护（a8）、施工容易度（a9）为定性指标，其他7项为定量指标。定量指标中，财务净现值、装机容量、年发电量、为效益型指标，而动态投资回收期、每千瓦投资额、移民数量、淹没耕地面积是成本型指标。经过初步研究，拟定了四个备选方案，各个方案的定量指标特征值见表1。

求 得 指 标 a1，a2，a3，a4，a5，a6，a7，a8，a9的 权 重 向 量 W=(0.1630，0.1413，0.1087，0.1087，0.0978，0.0870，0.0978，0.1087，0.0870)

3.2 投资方案模糊优选决策过程

3.2.1 求备选方案定性指标相对优属度矩阵

得到关于环境保护的优越性二元标度矩阵：

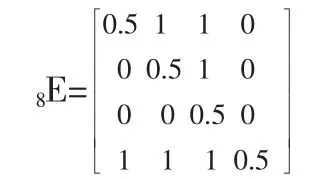
可判定8E为优越性排序一致性标度矩阵。对8E每行元素求和，根据各行元素之和得到关于对环境保护（a8）的优越性排序为：d4，d1，d2，d3。

以环境保护为标准，对各备选方案进行二元比较，求得有序二元比较矩阵的第一行为8A1=(0.5,0.60,0.75,0.8)，8A1中各元素的顺序按d4,d1,d2,d3排列。由公式（7）得相对优属度向量8r=(8rd1,8rd2,8rd3,8rd4)=(0.67,0.33,0.25,1.00)。

同理，得关于施工容易度的相对优属度向量：

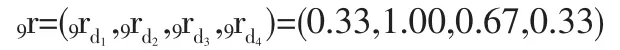
求得各方案对于各定性指标的相对优属度矩阵：

3.2.2 求备选方案定量指标相对优属度矩阵

根据公式（10）（11）可求得各方案关于定量指标的相对优属度矩阵如下：

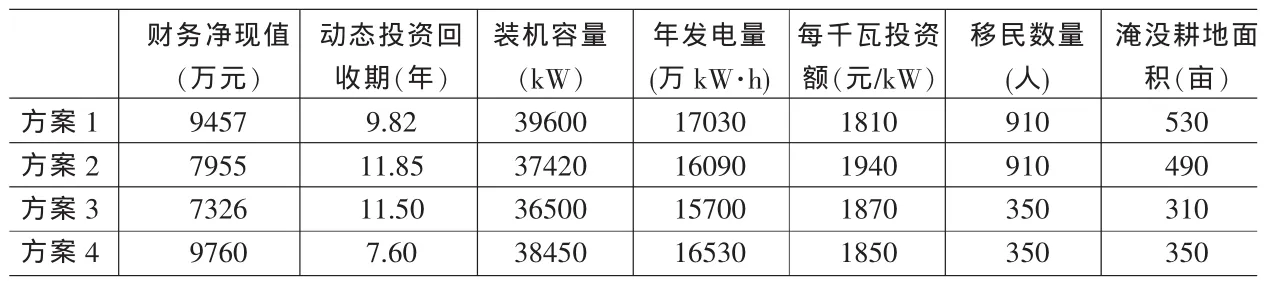
表1 投资方案定量指标特征值

3.2.3 优选决策

根据3.2.1和3.2.2的计算结果，得到优属度矩阵：

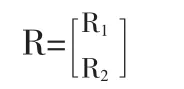
从优到劣共划分为5个级别，由公式（17）得到方案集属于各个级别的相对隶属度矩阵：

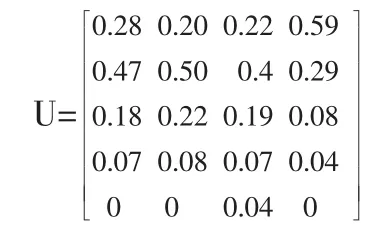
求得级别特征值的向量式：

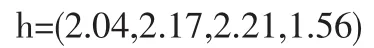
可得方案4为最优方案。

4 结论

对多种投资方案进行评价和优选在投资决策领域中具有重要意义。对备选方案进行评价需要建立科学的指标体系，指标体系中可包含定量指标和定性指标，如何综合定量指标和定性指标对备选方案进行综合评价是进行科学的投资决策所需要解决的问题。本文采用半结构性模糊优选方法综合评价投资项目的备选方案并进行多属性决策，按照相同的计算标准求得定量指标和定性指标特征值的优属度，并进行多级模糊优选求得最优投资方案。总之，本文为投资项目的决策提供了一种新方法，实例表明该方法是可行而有效的。

[1]Ribeiro R.A.Fuzzy Multiple Attribute Decision Making:A Review and New Preference Elicitation Techniques[J].Fuzzy Sets and Systems,1996,78(2).

[2]陈守煜.工程模糊集理论与应用[M].北京：国防工业出版社，1998.

[3]陈守煜.防洪调度多目标决策理论与应用[J].中国工程科学，2000，2(2).

[4]陈守煜.多目标系统半结构性决策理论与方法[J].辽宁工程技术大学学报（自然科学版），2001，20（5）.

[5]陈守煜.系统模糊决策理论与应用[M]大连：大连理工大学出版社，1994.