关于公司债违约传染研究

杨 星，潘亚舒

（暨南大学 经济学院金融系金融研究所，广州 510630）

1 关于双参数Weibull分布

瑞典工程师威布尔在上世纪30年代研究轴承寿命，结构强度和疲劳等问题时，给出了威布尔分布函数。并将其分为双参数和三参数威布尔分布。对于双参数Weibull分布，其密度函数、生存函数、危险率函数分别为;

密度函数：

其中：α＞0和λ＞0；λ为尺度参数，α为形状参数。

生存函数：

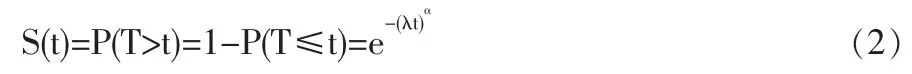
危险率函数：

对于双参数威布尔分布，危险率h(t)随α的变化而变化，且其可以利用概率很容易地推断出它的分布参数，因此它被广泛应用于各种生存分析的数据处理。而指数分布虽然在很多的研究领域也受到了欢迎，但因为其危险率是常数而限制了它的使用。因此我们选择双参数Weibull分布完成下面的工作。

2 双参数威布尔分布下的违约传染模型

2.1 假设条件

假设一：随机变量T服从W(α，λ)分布，则其密度函数表达式为：

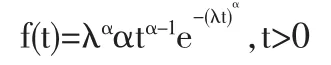
其中：α＞0和λ＞0；λ为尺度参数，α为形状参数。

假设二：假设有两家公司，它们的违约时间τi(i=1,2)服从W(αi，λi)。为便于计算，假设两家公司拥有相近的结构体系，即它们有相同的形状参数α=α1=α2。

违约时间τi(i=1，2)，设其密度函数、生存函数和危险率分别为：fi(t)，Si(t)=P(τi＞t)=e-λitαi和 hi(t)。 由此可知，在给定 τi＞t时，公司i的生存函数为：

若两家公司的违约时间相互独立，那么违约和生存完全由联合生存函数来描述：

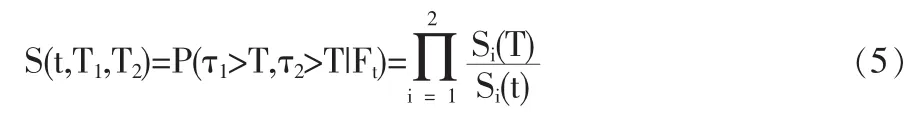
假设三：现实中，公司债的违约行为具有一定的传染性，尺度参数λi可看作是随机变量，即：

其中Yi(i=1，2)是连续、非负的随机变量，称作信任度调整系数。具有分布函数FY（y）=P(Y≤y)和密度函数fY(y)，其生存函数记为SY(t)。βi(i=1，2)为基于某种经济状态下的基准违约危险率，为大于零的常数。为便于计算，取：

假设四：到t时刻市场参与者获得的唯一的信息就是公司债是否违约，即条件滤子为{Ft}t≥0。

2.2 生存分析

2.2.1 初始生存概率

如果两家公司的违约时间τi在Y=y的条件下是相互独立的，则两家公司的联合生存函数为：

违约时间的联合条件密度为：

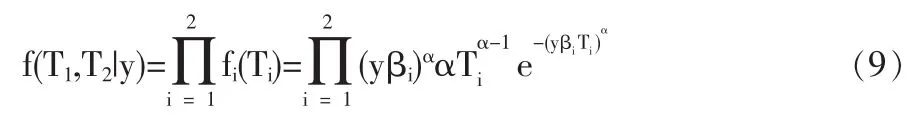
对（8）式两端取Y的数学期望，可得各公司的生存函数和它们的联合生存函数分别为：

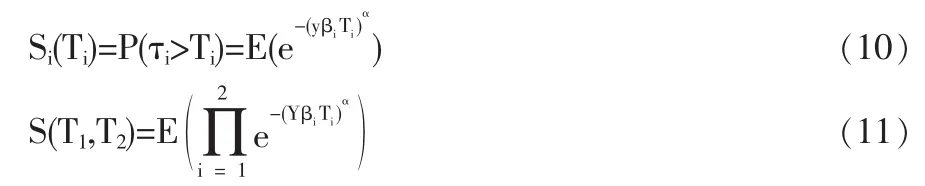
初始违约危险率为：

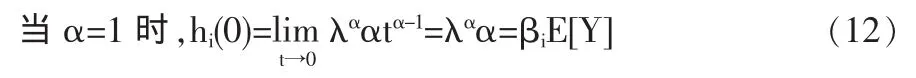
2.2.2 t时刻以后的生存分析

随着时间的推移，如果公司没有发生违约，此时的生存概率和违约危险率分别与（11）式和（13）式类似，但这里使用Y的条件概率分布。设到t时刻为止没有发生违约，即：τi＞t(i=1，2)，由假设（4）可知，违约危险率变为：

各个公司的生存概率以及它们的联合生存概率为：

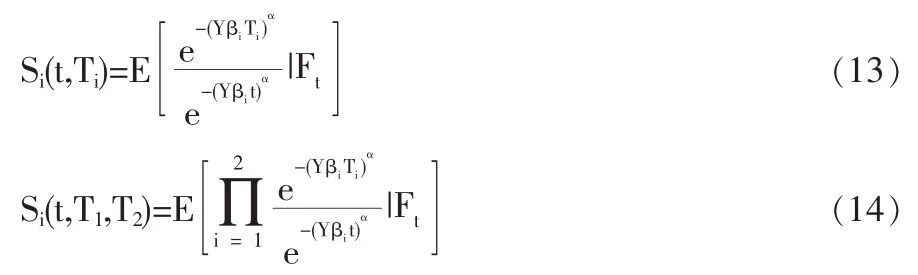
以FY,Ft(y)和fY,Ft(y)分别为Y在Ft下的条件分布和条件密度函数，其中FY,Ft(y)=P(Y≤y|Ft)，且要计算以上公式，需计算Y的条件密度。

2 违约危险率

由方程（8）和（9），可以得到 Y 在违约时间 τ1和 τ2不同状态下的条件密度。下面分两种情况进行讨论：

（1）两家公司直到t＞0时刻都生存

由（8）式及全概率公式，我们可得两家公司直到t＞0时刻都生存与Y≤y*的联合概率为：

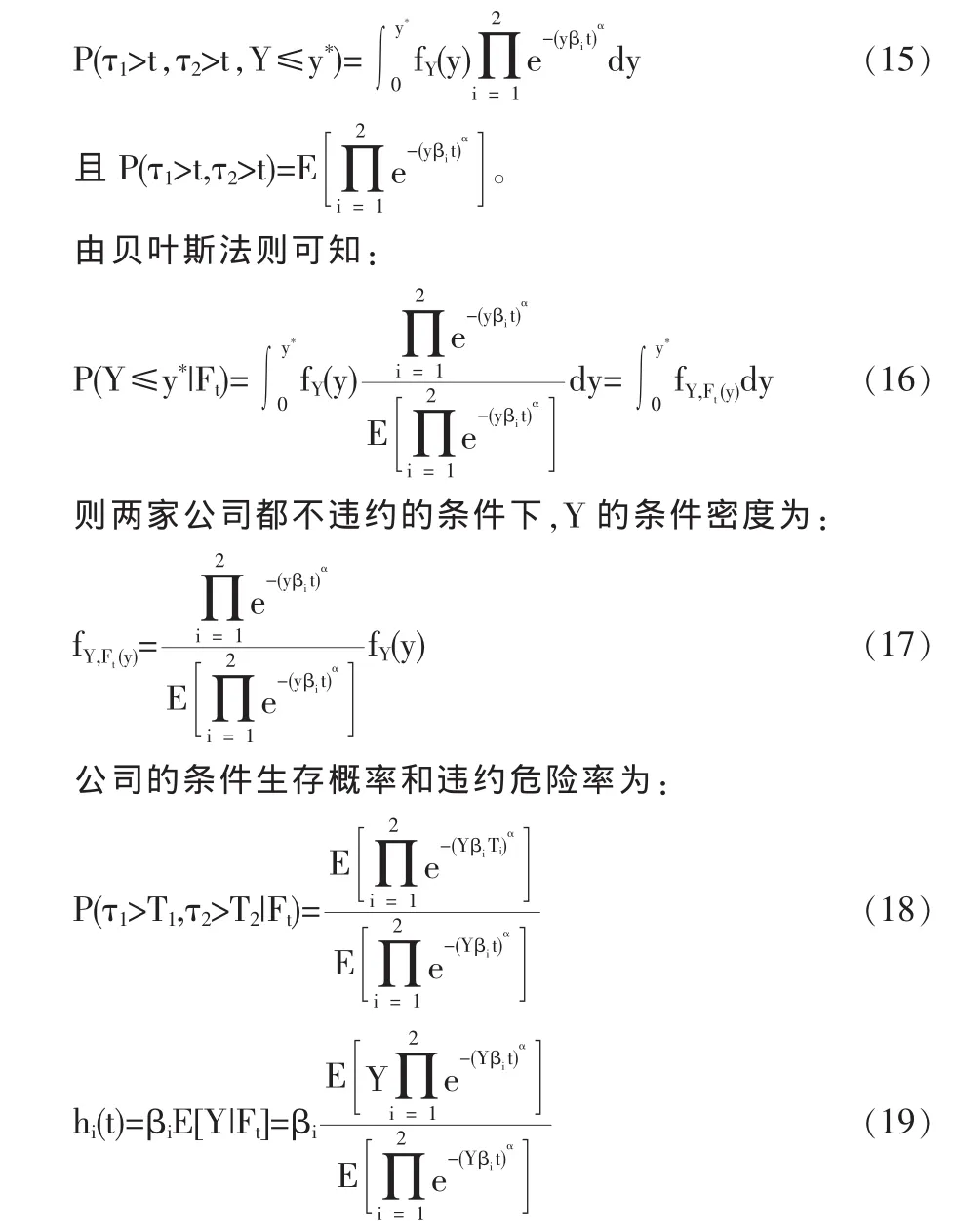
（2）只有一家公司违约而另一家公司不发生违约

设公司1在时刻T1违约，那么由（11）式可得τ1的密度为：

由上式及（9）式可得：

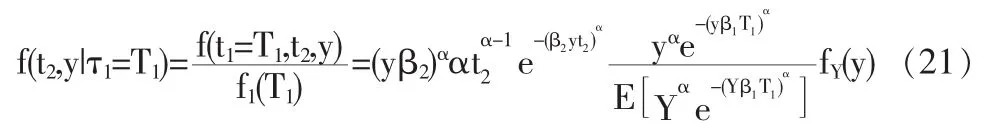
则在τ1=T1的条件下，公司1违约对联合密度的贡献为

由（22）式可知，y的条件传染密度可以分解成三部分的乘积：第一部分是公司生存直到发生违约，即在τ1≥T1，τ2≥T2的条件下产生；第二部分是有违约发生，即τ1=T1的条件下，产生与yα成比例的额外贡献；第三部分是y的强度。如果T1时刻公司1没有发生违约，只能得到第一、三部分贡献；当公司1违约时，就会增加Y的次幂，产生额外的贡献。

那么当公司1在T1时刻发生违约时，公司2的违约危险率由（13）和（22）可得：

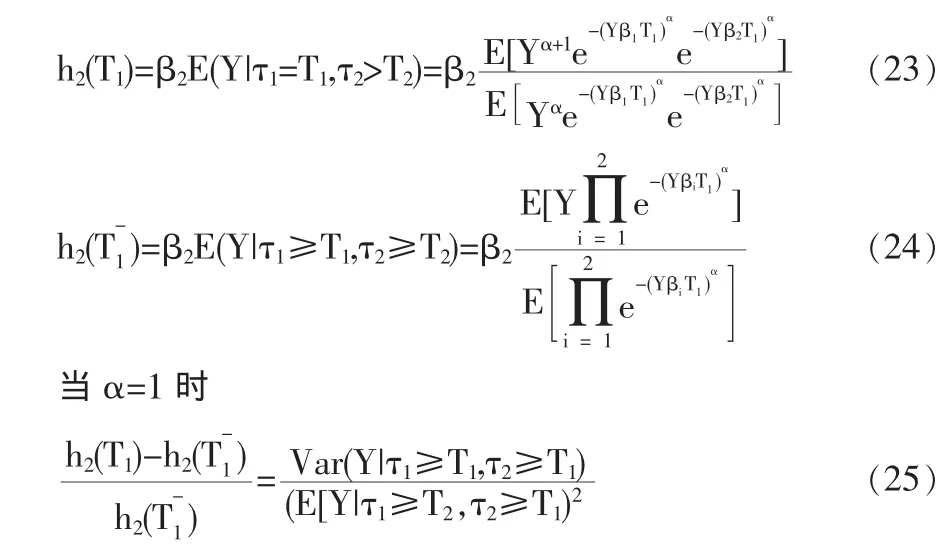
上式表明，违约危险率跳的相对大小总是非负的，信任度调整系数Y的不确定性决定了基于信息的违约传染影响的大小。

3 结论

当α=1时，上述模型的表达形式与 Schonbucher模型相同，因此，本模型推广了Schonbucher模型。且通过对（17）和（22）、（23）和（24）的比较，可知道一旦某个公司违约，Y 的最高次幂增大了（增加值为公司形状参数的大小），信任度调整系数的密度向更高风险值转移，使公司的生存前景变得更糟。但是这种跳跃并不是由于公司自身违约风险的变化而产生的，而是一种基于市场违约信息的传染。而传染的大小基于Y的不确定性，以及公司本身所特有风险因素，即不确定性越高（方差越大），由违约传递的信息也越多，传染的影响就越大。

[1]王倩，王煦逸.信用违约风险传染模型的比较研究[J].金融理论与实践，2007.

[2]Philipp J.Schonbucher.Information-Driven Default Contagion[C].Working Paper,Department of Mathematics,2003.