基于复合系统的城市可持续发展协调性评价模型

石培基，杨银峰，吴燕芳

（西北师范大学 地理与环境科学学院，兰州 730070）

0 引言

在当今城市化进程中，城市的人口、资源、环境、经济与社会发展往往出现失衡现象，如何协调区域人口、经济与社会发展同资源利用、环境保护之间的关系，以有效化解区域人口、资源、环境、经济和社会之间的矛盾成为摆在我们面前亟待研究的理论和现实问题。近年来，可持续发展系统的协调性的研究领域有大量的学者涉足，并取得了丰硕的理论成果。研究可持续发展问题最重要的方法莫过于系统论的方法，其中基于系统论的可持续发展系统协调性的研究方法主要集中于主成分分析和模糊隶属函数的系统协调性评价研究方法[1-3]以及基于层次分析法和协调度、协调发展度模型的系统协调性评价研究方法[4]等。但是大量的实证研究主要侧重于对同一个城市的不同时期的可持续发展协调性的测定与评价，而在各城市间人口、资源、环境、经济与社会系统的协调评价研究方面却显得相对薄弱。通过实践得出：在对城市间可持续发展的协调度进行横向测度与评价时，基于模糊隶属函数方法中的必须步骤——回归分析由于城市间的各系统发展存在差异，故拟合回归过程往往不能很好地实现，此方法移植性较差；而基于层次分析法模型中的专家咨询、打分过程在现实生活中一般较为繁杂，不易操作，并且该方法存在很大的主观性以及随机性等缺点。另外，以前的研究侧重于从人口与经济的关系、经济与环境的关系、经济与资源的关系等不同方面分别进行相对独立的研究，没有把上述五个因素放在同一个研究体系中，这在一定程度上割裂了它们之间互相依存、互为因果又互相促进的密切关系。

本文尝试通过因子分析和效益、平衡等理论构建的可持续发展协调性评价模型对城市可持续发展协调性进行评价研究，本模型可以有效地避免前面提到的两种系统协调性评价研究方法的缺陷，并在廖重斌提出的两个子系统协调度以及系统发展系数模型的基础上，进一步提出多个子系统协调度与协调发展系数模型，使人口、资源、环境、经济与社会五个方面在可持续发展系统研究体系中进行协调性综合评价得以实现，同时给出了相应的协调区间的划分及评价标准。

1 指标体系的构建及研究方法

1.1 指标体系的构建

一个城市的人口、资源、环境、经济和社会发展之间通过相互作用、相互影响和相互制约等关系而构成紧密相连的统一体，它是一个具有高度复杂性、多层次的复杂开放系统——可持续发展系统。相应的，人口、资源、环境、经济和社会成为可持续发展系统的子系统。对于各子系统间的协调性的定量研究就需要对各子系统分别建立相应的指标体系。

根据全面性、层次性、有效性和可操作性等指标选取原则，借鉴了以前学者的研究经验[7-9]，构建如下指标体系（见表1）。

1.2 研究方法流程

本文对可持续发展系统的协调性评价研究流程见图1所示，图中的“系统”均指可持续发展复合系统的子系统。

表1 人口、资源、环境、经济与社会系统协调性评价研究指标体系

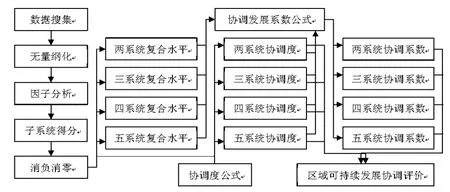
图1 研究方法流程图

2 人口、资源、环境、经济与社会系统的发展水平的测度

2.1 数据的无量纲化

由于各指标原始值量纲不同，数据值差异大，故为使各指标具有可比性，需要对原始数据进行无量纲化处理。本文采用极差标准化方法公式如下：

对于正指标：

式中，X'ij为Xij的标准化后的值；Xij为第i城市的第j指标的原始值；min{Xj}为第j指标的最小值；max{Xj}为第j指标的最大值。

2.2 分别对各子系统进行因子分析

因子分析是多元统计分析中常用的一种方法，基本思想是把所研究的众多反映同种信息的层叠变量提取出少数几个能够表示出原来的众多数据的绝大部分信息的公共因子，以达到简化数据，方便研究的目的。

利用统计分析软件SPSS13.0分别对各子系统的指标数据进行因子分析，采用主成分法提取公因子，并且要求提取主成分的累积方差贡献率大于85%。然后分别计算出各个主成分因子的特征值、方差贡献率以及各系统综合得分。

各因子的方差贡献率的计算公式：

式中，μi表示各因子的方差贡献率，λi表示各主成分因子的特征值。

各个子系统的综合得分值的计算公式：

式中，F为子系统综合得分，μi为第i主成分因子的方差贡献率，fi为第i个因子的值，n为因子的个数。

按照⑶、⑷两式可以分别计算出人口、资源、环境、经济与社会子系统的综合得分。

2.3 对得分值进行消负、消零处理

由于因子分析所求出的各系统综合得分存在负值，对于进行下一步的协调发展系数计算造成不便。因此需要事先对人口、资源、环境、经济与社会系统的得分值进行改造，这里采用线性比例变换的方法对它进行处理，又由于线性比例变换后的数据必有一数值为零，不适合用来计算协调发展系数，故这里借用功效系数的思想对它进一步的改造，改造后的各系统的综合发展水平得分区间为[n，1]（0＜n＜1）。 改造公式如下：

其中，Uij为改造后的第j子系统在第i行的发展水平得分值，Fij为改造前的第j子系统在第i行的得分值，m表示子系统个数。

2.4 复合系统的综合发展水平的计算

对于复合系统的两个子系统间的综合发展水平计算公式：

式中，U(i,j)为第i系统与第j系统组成的复合系统的综合发展水平值，Ui为第i系统的得分值，Uj为第j系统的得分值，α和β分别为第i与第j子系统在i，j两个子系统组成的复合系统中的权重。

三个子系统间的综合发展水平计算公式：

式中，U(i,j,k)表示第i、第j与第k三个子系统组成的复合系统的综合发展水平值，Ui、Uj、Uk分别为第i、第j与第k子系统的得分。γ、ф与φ分别为第i、第j与第k子系统在i，j，k复合系统中的权重值。

同理可以推出四个以及五个子系统组成的复合系统的综合发展水平计算的公式，在此不一一列举。

3 系统协调度与协调发展系数的计算

3.1 协调度的计算

根据效益理论与平衡理论的原理来构造协调度公式。所谓效益理论是指可持续发展的子系统保持同步发展，使综合效益最大。平衡理论是指各子系统保持一种平衡状态，任一子系统效益的增加不能以其他子系统效益的降低为代价。在这种平衡状态下，表现出的是一种复合效益。通常以子系统效益之和表示综合效益，之积表示复合效益。我们的目标就是在综合效益最大的基础上，求得最大复合效益[10]。构造以下公式：

Ui、Uj分别为第 i、第 j系统的发展水平。

用平均效益指数代替综合效益指数，对C进行标准化处理，可得：

其中，K为协调系数，且K≥2。可以验证0＜C≤1，在此把C定义为复合系统的协调度。

依次类推，可分别得出三、四、五个子系统的协调度计算公式，在此由于篇幅限制，故公式略。例如五个子系统的协调度计算公式如下：

式中，Ui、Uj、Uk、Ul、Um分别是第 i、j、k、l、m 的发展水平。

根据复合系统的协调度的大小，可以看出复合系统的各子系统间发展的协调与否。在此给出协调区间划分以及系统协调度评价表（见表2）。

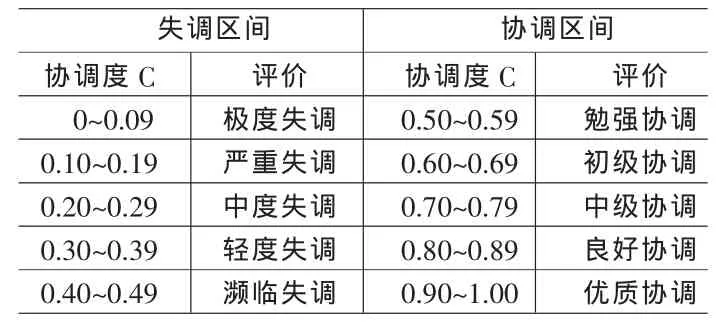
表2 系统协调度区间划分及评价标准

3.2 系统的协调发展系数

系统的协调度固然能够较好地反映出各个子系统之间的协调状况，却无法很好的表示出复合系统协调发展的综合效益或者综合发展水平。根据学者廖重斌的研究，构建协调发展系数公式：

式中，D为复合系统协调发展系数，C为系统协调度，U为复合系统综合发展水平，其值可由⑹、⑺等公式求得。最后，根据(11)式可以分别求出2个、3个、4个以及5个子系统间的协调发展系数值，从而，可以根据各值的大小对于系统间的协调发展情况进行评价。

由于子系统较多，对于各个子系统间的评价过于冗长，在此不分别对具体几个子系统协调发展系数进行评价分类，在此，给出一般的协调发展系数的区间划分以及系统协调发展系数的评价表（见表3）。

表3 系统协调系数的区间划分与协调发展评价标准

4 结论

本研究运用因子分析与效益、平衡等理论构建的城市可持续发展协调性评价研究模型，能够较好地避免当前常用的协调性评价模型在城市间横向比较的应用中存在的回归分析拟合较差以及层次分析操作复杂、主观性强等缺点，并且能够对可持续发展系统的多个子系统间的协调发展情况进行评价研究，最后给出了协调度及协调发展系数的区间划分和评价标准；另外，该模型也可应用于同一区域的不同时期的可持续发展系统的协调性的评价研究。

[1]穆光宗.可持续发展中的人口因素[J].人口学刊,1996,(5).

[2]王胜今,齐艺莹.我国人口、资源与环境经济学学科发展的思考[J].吉林大学社会科学学报,2004,(6).

[3]王维国.协调发展的理论与方法研究[M].北京:中国财政经济出版社,2000.

[4]戴西超,谢守祥,丁玉梅.技术—经济—社会系统可持续发展协调度分析[J].统计与决策,2005,(3).

[5]刘小林.区域人口-资源-环境与经济系统协调发展的定量评价[J].统计与决策,2007,(1).

[6]廖重斌.环境与经济协调发展的定量评判及其分类体系——以珠江三角洲城市群为例[J].热带地理,1999,19(2).

[7]张坤民,何雪炀,温宗国等.中国城市环境可持续发展指标体系研究[J].生态经济,2000,(7).

[8]秦耀辰,张二勋,刘道芳.城市可持续发展的系统评价——以开封市为例[J].系统工程理论与实践,2003,(6).

[9]张广毅.基于灰色聚类法的城市可持续发展水平测度分析[J].生态经济,2009,(7).

[10]陈静,曾珍香.社会、经济、资源、环境协调发展评价模型研究[J].科学管理研究,2004,22(3).