灰色预测方法的应用

李恩临

(1.哈尔滨工程大学 经济管理学院，哈尔滨 150001；2.哈尔滨商业大学 计算机与信息工程学院，哈尔滨 150028)

近年来，随着国际航运市场的发展和二手船船价的变化，二手船的经营贸易相当活跃，我国企业购置国外二手船活动也十分频繁。这主要是由于新造船舶周期长，成本太高，通常不被采纳，而购置国外二手船具有价格较低、交船周期短等优点，受到了包括中小企业在内的大多数航运企业的青睐。由于二手船价格存在周期性波动，因此本文采用灰色预测法对二手船船价进行预测,为航运市场经营者及投资者把握市场方向，规避价格风险具有重要的现实意义。

1 GM（1,1）模型

GM模型中最常用的是一阶、一个变量的微分方程模型GM(1,1)，其原理是通过对原始数据序列作一次累加生成(1-AGO)，从而使生成数据序列呈现一定规律，进而构造预测模型。具体步骤如下：

（1）设原始数据列为一组一维的非负数列X（0），

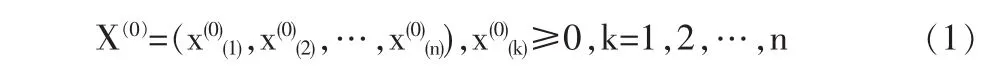
（2）构造新数列 X(1)，X(1)由 X(0)一次累加生成，

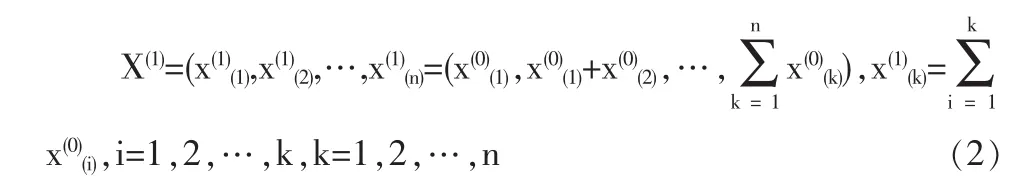
（3）生成 X(1)的紧邻均值生成矩阵 Z(1)，

（4）建立微分方程：

其中a和b分别为GM(1,1)的发展参数与灰色内生控制参数。该方程为GM（1,1）模型的基本形式。

用最小二乘法可以得到x(0)+az(1)=b的参数向量，如果=[a，b]T，则

（5）GM(1,1)模型X(0)(k)+aZ(1)(k)=b的时间相应序列为：

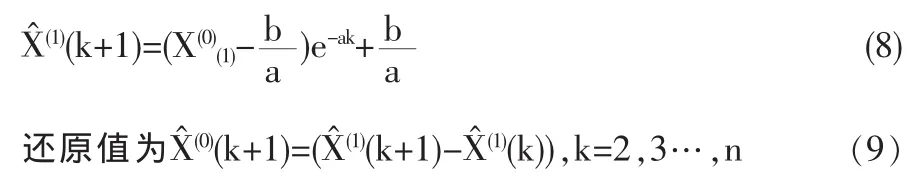
GM（1,1）模型检验一般有残差检验、关联度检验和后验差检验。

2 实证分析

2.1 二手船价格预测模型

本文以十年船龄30000dwt干散货船为研究对象，采用GM（1,1）模型建立1999年到2004年二手船价格模型，测算其精确度并进行预测。

（1）以1999年为起始点，即在该点t=1，于是有原始数据序：

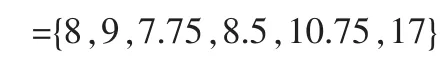
年份价格199982000920017.7520028.5200310.75200417

（2） 计 算 累 加 数 列 ， 得 X（1）：X（1）={X（1）（t）|t=1，2， … ，6}={8，17，24.75，33.25，44，61}

（3）计算 X（1）的紧邻均值生成矩阵 Z（1）：

（4）计算 GM(1,1)模型 X(0)(k)+aZ(1)(k)=b 的参数

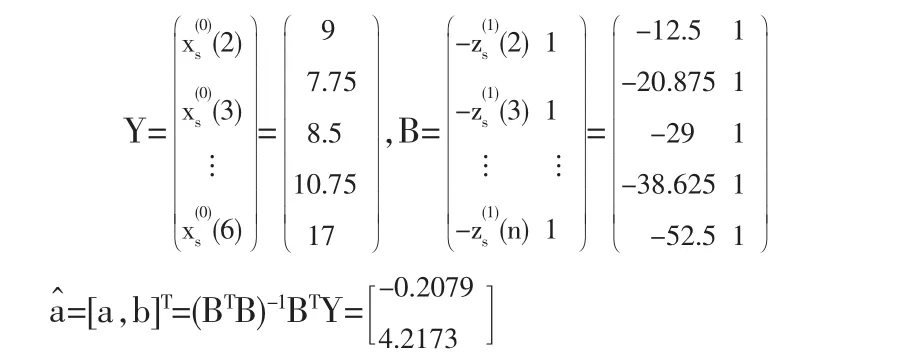
二手船价格的GM（1,1）模型的时间相应式：

2.2 模型检验

本文主要通过后验差检验方法。由(10)式及（9）式得：模拟序列残差序列ε(0)={0,-2.46,0.30,1.41,1.45,-1.99}，残差平均值，残差标准差S2=2.13，原始数据的平均值，原始数据的标注差 S1=7.86

3 模型应用

使用上述模型对未来6年二手船价格进行预测，得到2005年到2010年预测值，本文采用matlab7.4作为计量软件，所用程序见附录。结果如下：

200728.02200834.49200942.46201052.27年份预测值实际值200518.4819200622.7623

比较2005和2006两年的预测值与实际值，通过计算平均绝对误差、平均相对误差、均方根误差，对模型的预测精度进行度量分析：

平均绝对误差、平均相对误差、均方根误差都十分小。由此可知模型预测的精度很高。

4 结论

根据1999年至2004年的二手船价格数据建立的GM(1,1)模型通过了相关检验，通过计算平均绝对误差、平均相对误差、均方根误差，对模型的预测精度进行度量分析表现出了极高的精度，因此该模型适用于二手船价格的预测。

[1]Michael Beenstock,Andreas Vergottis.An Econometric Model of the World Market for Dry Cargo and Shipping[J].Applied Econom⁃strics,1986,(21).

[2]Glen.D.The Market for Secondhand Ships Further Results on Efficiency Using Integration Analysis[J].Maritime Policy and Man⁃agement,1991,(24).

[3]Alizadeh,A.H.，Nomikos,N.K.The Price-volume Relationship in the Sale and Purchase Market for Dry Bulk Vessels[J].Maritime Policy and Management,2003,(4).

[4]Syriopoulos.T.，Roumpis,E.Price and Volume Dynamics in Sec⁃ond-hand Dry Bulk and Tanker Shipping Market[J].Maritime Pol⁃icy and Management,2006,(5).

[5]蔡立明，卢春霞.ARIMA模型在二手船价格预测中的应用[J]，中国水运,2008,(6).

[6]李建华.基于BP神经网络的二手船船价指数预测研究[D].大连，大连海事大学,2008.

[7]曾波.居民消费价格指数的GM(1,1)模型预测[J],统计与决策,2009，（13）.