基于有限元法对小椭圆度连续管挤毁压力研究

董昌乐,聂翠平,韩新利,郝 宁

(1.西安石油大学,西安710065;2.中国石油集团石油管工程技术研究院,西安710065;3.川庆钻探工程有限公司长庆指挥部,西安710200)

基于有限元法对小椭圆度连续管挤毁压力研究

董昌乐1,2,聂翠平1,韩新利2,郝 宁3

(1.西安石油大学,西安710065;2.中国石油集团石油管工程技术研究院,西安710065;3.川庆钻探工程有限公司长庆指挥部,西安710200)

连续管在滚筒上缠绕和卸绕,由最初的近乎理想圆不断地椭圆化。与理想圆相比,椭圆化在很大程度上降低了连续管的挤毁压力。建立了小椭圆度连续管的有限元模型,并加载分析,将其结果与试验数据相比较,可以发现,该模型有着较高的可靠性。此外,通过该模型计算ø88.9 mm×4.83 mm、材料屈服强度514 MPa连续管不同椭圆度下的挤毁强度,并回归该规格连续管挤毁强度与椭圆度关系式。

连续管;挤毁压力;有限元分析

Abstract:As the coiled tubing is cycled on and off the reel,it becomes oval from perfectly initially round CT at its first use.Its oval deformation decreased the collapse failure pressure significantly,compared with perfectly round tubing.Finite Elements Models were built,and the conclusions based on FEM showed satisfactory agreement with experimental data.In addition,the collapse pressure forΦ88.9 mm×4.83 mm and 514 MPa yield pressure CT with different ovality was calculated.The equation between collapse pressure and ovality is shown.

Key words:coiled tubing;collapse pressure;finite element analysis

随着石油管的不断发展,连续管已成功应用于石油工业[1-3]。但是,连续管的服役条件恶劣,如果连续管服役环境压力足够高,连续管将被挤毁,这不仅会引起井控问题,还会导致大量的打捞作业。连续管用户需要的是一个可靠的挤毁压力安全标准。理想圆连续管挤毁压力的理论得到了长足的发展,而椭圆化连续管挤毁压力理论却没有很好地发展。刚生产的连续管近乎理想圆,椭圆度很小(≤0.5%),随着在滚筒上缠绕和卸绕,由于塑性变形使得理想圆的连续管椭圆化。缠绕的次数越多,椭圆度将增加。与理想圆相比,椭圆化在很大程度上降低了连续管的挤毁失效压力[4]。但是,实物试验评价费用高、周期长,因此,建立椭圆化连续管挤毁压力有限元分析模型,既可保证较高精度,又能缩短周期和减少费用,对评价连续管抗挤毁性能至关重要。

1 有限元模型建立与计算[5]

椭圆度定义:在石油和天然气工业中,“椭圆度”用于描述管材的不圆程度。其定义式为

式中,dmax为最大直径;dmin为最小直径;dave为平均直径,dave=(dmax+dmin)/2。

由于连续管的径向长度与其轴向长度相比很小,可以采用平面应力方法对其进行力学分析。图1～2所示为连续管无轴向力和有轴向力作用下的挤毁压力力学模型。

图1 无轴向载荷连续管挤毁压力力学模型

图2 轴向拉力作用下的连续管挤毁压力力学模型

1.1 有限元模型及网格划分

考虑到问题的对称性,有限元建模时,将连续管建成1/4对称模型,可以在保证求解精度的前提下减少有限元计算时的节点和单元总数,提高计算效率。通过压缩y轴坐标或x轴坐标来定义椭圆度η。

建立ø88.9 mm×4.83 mm连续管有限元模型。无轴向力时,选用 PLANE 2单元划分网格,PLANE 2为二维实体单元,可应用于平面问题(平面应力和平面应变)和轴对称单元。该单元由6个节点定义,每个节点有2个自由度:x、y方向。有轴向载荷时,选用SOLID 45单元划分网格,SOLID 45为三维实体单元,可应用于轴对称问题,该单元由8个节点定义,每个节点有x、y、z方向3个自由度。图3为无轴向力作用时,椭圆度η=0.14%连续管的有限元模型;图4为有轴向载荷时,椭圆度为η=0.24%连续管的有限元模型。

图3 无轴向拉力作用的连续管有限元模型

图4 有轴向拉力作用的连续管有限元模型

1.2 边界条件

有限元模型网格划分好后,定义边界条件和加载方式。由于对称性,在对称边界施加对称位移约束,轴向拉力和外压以分布载荷的形式施加在连续管端面和管体外壁。图5为无轴向拉力作用,椭圆度η=0.14%连续管,外压p=51.05 MPa时有限元模型Von Mises应力云图;图6为椭圆度η=0.24%连续管,轴向拉力F=53 kN、外压p=49.33 MPa时有限元模型Von Mises应力云图。

图5 椭圆度η=0.14%,外压p=51.05 MPa时连续管有限元模型Von Mises应力云图

图6 椭圆度η=0.24%,轴向拉力F=53 kN,外压p=49.33 MPa时连续管有限元模型Von Mises应力云图

2 有限元模型计算结果与试验数据比较

根据实物试验测得的不同椭圆度连续管的屈服强度,以及外压挤毁试验值,调整有限元模型的椭圆度、外压值及轴向载荷。将所得结果与实物试验值进行比较,结果如表1。

表1 有限元模型计算结果与试验数据比较

由表1发现,与实物试验值相比,模型计算的挤毁强度具有很高的可靠性。12个试样中,模型关联误差仅有1个＞0.1,其余11个均＜0.1,且平均关联误差γ=0.060,因此可以将该模型应用于工程实践。

有限元模型可以方便快捷地计算具有一定椭圆度连续管的挤毁压力,而且具有较高的可靠性。图7和表2为ø88.9 mm×4.83 mm、材料屈服强度为514 MPa的连续油管,无轴向载荷作用,不同椭圆度有限元计算结果。

在有限元模型计算基础上,通过2次非线性回归分析,可得 ø88.9mm×4.83mm、材料屈服强度514 MPa的连续管挤毁强度与椭圆度的关系式为

式中,PYp为挤毁强度,MPa;η为椭圆度,%。

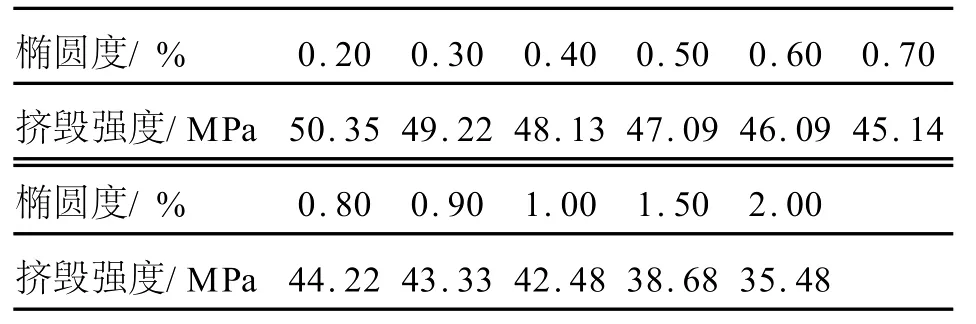
表2 不同椭圆度连续管挤毁强度有限元模型计算值

图7 连续管挤毁强度椭圆度曲线(基于有限元模型计算)

3 结论

1) 建立的有限元模型,计算结果与实物试验值误差较小,具有较高的可靠性,能够满足工程需求。

2) 随着椭圆度的增大,连续管的挤毁强度降低。

3) ø88.9 mm×4.83 mm、材料屈服强度514 MPa的连续管挤毁强度与椭圆度的关系式为PYp=1.5793η2-11.683η+52.569 。

(注:连续管实物试验数据来源于SPE36338)

[1] 于小波,许国林,杨 超.锥形连续管技术[J].石油矿场机械,2008,37(7):79-82.

[2] 杨 高,罗 刚.连续管缠绕力学研究[J].石油矿场机械,2010,39(5):10-13.

[3] 毕宗岳,井晓天,金时麟,等.连续油管性能研究与产品开发[J].石油矿场机械,2010,39(6):16-20.

[4] Yang Yong S.Collapse Pressure of Coiled Tubing Under Axial Tension[R].SPE,36338.

[5] 王庆五,左 昉,胡仁喜.ANSYS 10.0机械设计高级应用实例[M].2版.北京:机械工业出版社,2006.

Collapse Pressure of Small Ovality Coiled Tubing Based on Finite Element Analysis

DONG Chang-le1,2,NI Cui-ping1,HAN Xin-li2,HAO Ning3
(1.Xi’an Shiyou University,Xi’an710065,China;2.CN PC Tubular Goods Research Institute,Xi’an710065,China;3.Changqing General Drilling Company,Chuanqing Drilling Engineering Co.,Ltd.,Xi’an710200,China)

TE933.8

A

1001-3482(2010)11-0022-03

2010-05-17

董昌乐(1982-),男,安徽六安人,硕士研究生,主要研究方向为油气井管柱力学,E-mail:dcl1227@163.com。