ARI MA模型在我国全社会固定资产投资预测中的应用

李 惠

(河北经贸大学,河北石家庄 050061)

一、引言

改革开放以来,我国的经济发展取得了举世瞩目的成就。我国的全社会固定资产投资总额也持续增加：1980年仅为 910.9亿元;1993年首次突破 10000亿元达到 13072.3亿元;到 2006年则猛增至 109998.2亿元。尤其是进入 21世纪以来,随着中国加入WTO,外商投资大量增加,推动了经济政策的调整与完善,也给经济与投资增长增添了活力。对全社会固定资产投资有影响的因素很多,而这些因素彼此之间又有着错综复杂的联系。本文从动态角度考察,把我国全社会固定资产投资总额看成是一个时间序列,利用历史数据分析并得到其规律性,从而预测其未来值。

二、ARIMA模型简介

一个随机时间序列可以通过一个自回归移动平均过程产生,即运用时间序列的过去值、当期值及滞后扰动项的加权和建立模型来“解释”时间序列的变化规律。如果该序列是平稳的,即它的行为并不会随着时间的变化而发生变化,那么我们就可以利用该序列过去的行为来预测其未来,这就是随机时间序列分析模型的优势所在。

传统的时间序列模型只能描述平稳时间序列的变化规律,但大多数经济时间序列都是非平稳的,它们的数字特征,如均值、方差和协方差等是随着时间的变化而变化的,也就是说,非平稳时间序列在各个时间点上的随机规律是不同的,这就难以通过序列已知的信息去掌握序列整体上的随机性。在实践中遇到的金融和经济问题大都是非平稳的,例如 GDP、消费、收入、货币需求、价格水平和汇率等。为此,需要先把一个非平稳的时间序列通过差分的方法将它变换为平稳的,然后用一个平稳的 ARMA(p,q)模型作为它的生成模型,则我们说该原始时间序列是一个自回归单整移动平均时间序列,记为ARIMA(p,d,q),其基本模型包括三种：自回归(AR)模型;移动平均(MA)模型;自回归求积移动平均(ARIMA)模型,其中ARIMA模型使用包括自回归项(AR项)、单整项和MA移动平均项三种形式对扰动项进行建模分析,使模型同时综合考虑了预测变量的过去值、当前值和误差值,从而有效地提高了模型的预测精度.

三、建立ARIMA模型的一般方法

1.对原始序列作平稳性检验,若该序列被判定为非平稳的,则可以通过差分运算或其它运算方法对其进行变换,从而得到平稳的时间序列。

2.确定 ARMA(p,q)模型的阶数 p和 q,在这里可以通过计算能够描述序列特征的一些统计量,如自相关(ACP)系数和偏自相关(PACP)系数来确定 p和q的值,注意在初始估计中选择尽可能少的参数。

3.估计模型的未知参数,并通过参数的T统计量检验其显著性,以及模型的合理性。

4.进行诊断分析,以证实所得模型确实与所观察到的数据特征相符。

在第 3、4步,需要一些统计量和检验来分析在第 2步中模型形式选择是否合适,所需要的统计量和检验如下：

1.检验模型参数显著性水平的 t统计量;

2.为保证 ARIMA(p,d,q)模型的平稳性,模型的特征根的倒数小于 1;

3.模型的残差序列应当是一个白噪声序列。

四、ARIMA模型的实际应用

全社会固定资产投资的影响因素很多,如经济基础、人口增长、资源、科技、环境等诸多因素都对其构成影响,而这些因素之间又有着错综复杂的关系。因此要想运用结构性的因果模型对群社会固定资产投资进行分析和预测往往比较困难。可以试着将历年的全社会固定资产投资作为一个时间序列,分析其变化规律,从而建立预测模型。

本文对 1980—2007年的 28个年度我国全社会固定资产投资数据进行分析,数据来源于《中国统计年鉴》,为了检验该模型的正确性,现在可以用前 25个数据参与建模,并用后 3年的数据检验拟合效果。最后对我国2008年与 2009年的全社会固定资产投资进行预测。

图1

1.观察时间序列原始数据图1为 1980—2004年25年时间我国全社会固定资产投资总额。观察到曲线明显向右上方倾斜,而且前后波动幅度明显不一致,这说明该序列存在增长趋势,并且存在异方差。

再对原始数据进行单位根检验,见表1。

表1

从表1可以看出,原始数据没有通过 ADF检验,因此,该时间序列是非平稳的时间序列。这一结果进一步证实我国全社会固定资产投资总额的变化是受多因素影响而不能采用固定模式进行分析预测。

2.对原始数据进行平稳化处理

利用 EViews软件,对原数据取对数：

图2 取对数后自相关与偏自相关图

可见取对数之后的序列依然非平稳,样本自相关函数拖尾,样本偏自相关函数截尾,其序列图有明显的增长趋势。

对已经形成的对数序列进行一阶差分,然后进行ADF检验(见表2)。

由于该序列依然非平稳性,因此需要再次进行差分,得到如图3所示的折线图。

根据对数一阶差分时所得 AIC最小值,确定滞后阶数为 4,然后对对数二阶差分进行 ADF检验(见表3)。

表2 对数一阶差分的ADF检验

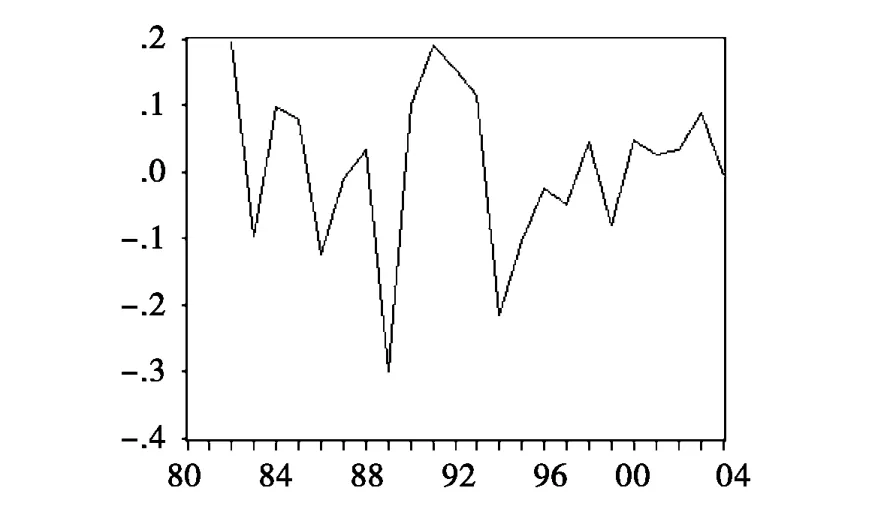
图3

结果表明对数二阶差分后的序列具有平稳性,因此ARIMA(p,d,q)的差分阶数 d=2。二阶差分后的自相关与偏自相关图如图4：

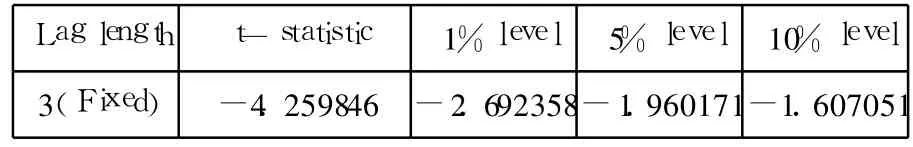
表3 对数二阶差分的ADF检验单位：亿美元

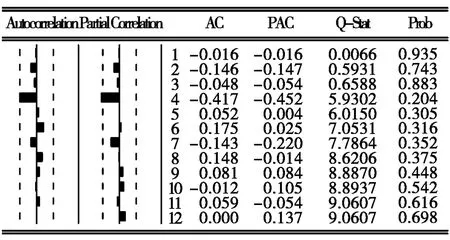
图4 对数二阶差分后自相关与偏自相关图

3.ARIMA(p,d,q)模型的建立

通过分析本文选用 ARIMA(p,d,q)模型,其中 d是差分的次数或单整的阶数,已经由上面单位根检验中得出d=2。p是自回归的阶数;q是移动平均的阶数。ARIMA(p,d,q)模型的识别与定阶可以通过样本的自相关与偏自相关函数的观察获得。由图4可见,自相关系数与偏自相关系数在滞后阶数为4之后一直处于置信区间以内,可以考虑 p=4和 q=4。建立 ARIMA(4,2,4)模型：

MA(4)=0.9552445053,BACKCAST=1986](其中 X为原始数据)。

上述模型中各系数均通过 T检验及整个方程也通过了F检验,说明所建立的模型是显著的。

4.残差图分析

上述 ARIMA(4,2,4)模型的残差图如图5所示。残差图完全符合时间序列模型拟合的很好的条件,可以明确地说该模型拟合得比较成功。

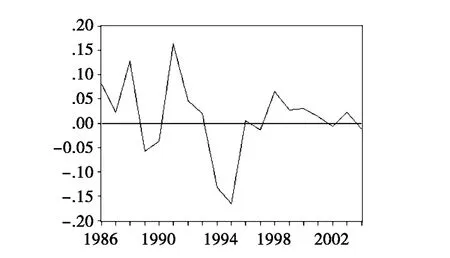
图5 ARIMA(4,2,4)模型的残差图

5.模型的预测

表4给出 2005—2007年全国全社会固定资产投资额实际值与预测值的计算结果以及其相对误差。

从表4中可以看出,预测结果的相对误差均小于5%,结果相当令人满意,说明所建模型具有良好的预测效果。我们利用此模型对 2008年和 2009年我国全社会固定资产投资额进行预测,最终的预测结果为 160012.5亿元和 190477.1亿元。建议政府在引导投资时应合理安排投资比例,合理运用投资金额和投资机会,从而促进经济健康发展。

ARIMA模型在短期内预测比较准确,随着预测的延长,预测误差会逐渐增大,这是 ARIMA模型的缺陷。但是与其他的预测方法相比,其预测的准确度还是比较高的,尤其在短期预测方面。

表4 用所建立的模型预测的结果及相对误差单位：亿元

[1]郝晶,沈红燕,陈希.我国固定资产投资的 ARIMA模型分析与预测[J].数学理论与应用,2009(6).

[2]漆海波.1997—2002年中国固定资产投资研究[J].应用研究,2003(11).

[3]师思.ARIMA模型在固定资产投资变化率预测中的运用[J].统计与决策,2009(10).

[4]高铁梅.计量经济分析方法与建模[M].北京：清华大学出版社,2006：302—347.

[5]中国统计年鉴.2008.