浅正弦波纹圆板大挠度问题的摄动解法✳

袁 鸿,龚胜海,吴立彬

(暨南大学重大工程灾害与控制教育部重点实验室,应用力学研究所,广东广州 510632)

近几十年来,随着科学技术的突飞猛进,弹性元件的发展异常迅速,广泛应用于自动控制、测量仪表、真空技术、机械工业、电力工业、交通运输及原子能工业等领域.在仪器仪表中应用也十分广泛,是仪器仪表的主要基础元件之一.常用的有:波纹圆板、波纹管、振动弦、片簧、压力弹簧管、热敏双金属等.

波纹圆板作为一种弹性元件,由于具有灵敏度高、线性度好等优点,使它的应用范围极其广泛,在传感器中占有重要地位,是多种传感器和精密仪器的核心.波纹膜片以其独特的优点在各种技术领域里广泛使用,尤其是作为低压敏感元件被广泛应用于精密仪器仪表和传感器中.自从 Heresey[1]和Griffith[2]各自展开了对波纹圆板的实验和理论研究以来,世界各国的科学家[3-16]在这方面做了大量的工作;然而,得到的解答主要是数值解,这种弹性元件的理论研究至今还不是很充分.造成这种状况的主要原因是,波纹膜片本身形状复杂,参数很多,特别是大挠度非线性微分方程组在数学上求解极其困难.现有的理论解中,绝大多数成果都是从正交异性板理论出发得到的[17-22],用正交各向异性板处理波纹圆板的问题是一个有效的方法,能同时讨论各种形状的波纹圆板.然而,简化本身也带来一些不足:第一,对于波纹圆板,它得到的特征缺少中心挠度的偶次项,因而不能反映载荷反向时波纹圆板不同的刚度特征;而当波纹数较少及挠度较大时,这种差别可以是显著的.第二,它的解答不能用于研究波纹圆板的应力分布和局部失稳现象.第三,它只能解决分段均匀的波纹圆板问题(即每个波的波纹深度、波纹形状必须一致),而不能解决带有边缘波纹、波纹深浅不同的波纹壳问题.使用薄壳非线性理论进行分析能避开以上不足,但由于壳体大挠度方程本身的非线性和复杂性,增加了求解难度.陈山林[23]用修正迭代法求解了波纹圆板的大挠度方程,得到了具有光滑中心的浅正弦波纹圆板在均匀载荷下的弹性特征,为了得到一个较好的初始近似,引入了初始近似修正系数.袁鸿[24]采用摄动法和幂级数方法,研究了具有光滑中心的锯齿形和梯形波纹圆板的弹性特征,得到了含中心挠度二次项的设计公式.

本文借鉴文献 [24]的研究思路,基于扁壳的非线性大挠度理论,用摄动法求解了浅正弦波纹圆板的大挠度方程.选取无量纲中心挠度作为摄动参数,将描述波纹圆板的非线性微分方程组化为一系列线性微分方程组.对于中心平台部分,描述各阶摄动的线性微分方程组成为通常的欧拉方程,可以得到精确解;对于波纹部分,不能直接得到各阶摄动的精确解,采用幂级数方法求解.最后根据边界条件、连续条件和摄动条件,将摄动问题化为线性代数方程组进行求解,得到具有中心平台的浅正弦波纹圆板在荷载下的弹性特征.

1 浅正弦波纹圆板大挠度问题的摄动解法

无量纲化轴对称旋转扁壳的基本方程[3,25]是

其中:

式中:r是径向半径;T*是变形前壳体子午线与水平方向的夹角;U*为子午线的转角;F是应力函数;E和g分别是弹性模量和泊松比;P0和 Q0分别是均布载荷及中心集中载荷;h表示波纹部分及中心平台的板厚;a是波纹圆板的半径.

设有波纹圆板,它由一个光滑中心平台和浅正弦波纹两部分组成,中心平台半径为 b,波长为 L0,波幅为 H,如图1所示.

图1 浅正弦波纹圆板的轴向截面Fig.1 Geometry of circular plate with shallow sinusoidal corrugation

2)滑动固定情形

基本方程 (2)和 (5)是非线性的,对方程中的未知函数U,g和外荷载 P做摄动展开

式中:X是摄动参数.将上面的摄动展开式代入基本方程 (2)和 (5)中,比较方程两边X的同次幂的系数,得到各级摄动展开后的微分方程组

式 (8)中,当求和号的终值小于初值时,不求和.对于中心平台部分,T=0,此时方程 (7)和 (8)就变成了通常的欧拉公式,可以求得精确解析解;对于浅正弦波纹部分,式 (7)和 (8)虽然是线性的,但是求不出解析解,这个时候可以得到幂级数解.下面对光滑中心和波纹部分分开讨论.

1.1 中心平台部分的求解

对于光滑中心部分,0≤R≤R1=b/a,T=0.将摄动展开式 (6)代入条件 (3)中,得到

此时一阶摄动方程 (7)和 (8)在式 (10)下的解(L=1)为

而二阶摄动方程 (7)和 (8)在式 (9)下的解(L=2)为

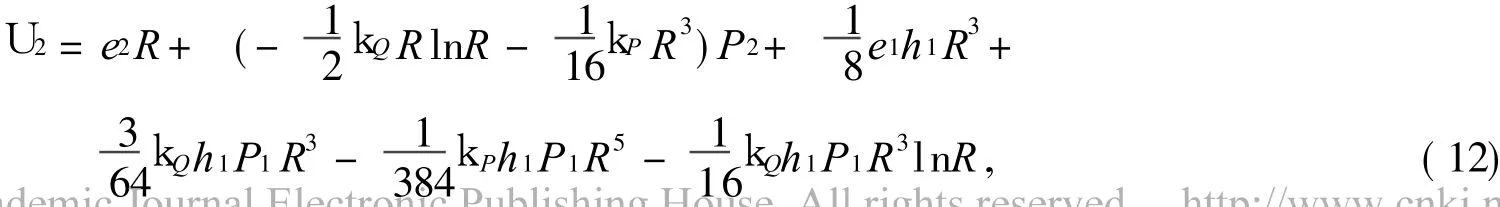
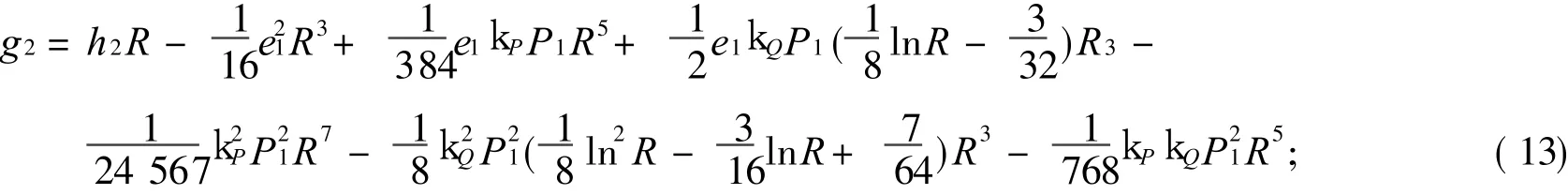
三阶摄动方程 (7)和 (8)在式 (9)下的解 (L=3)为

式(10)～(15)中,e1,h1,P1,e2,h2,P2,e3,h3,P3是待定常数,由外边界条件、连续条件和摄动条件决定.

1.2 波纹部分的求解

对于图1所示的浅正弦波纹部分,R1≤R≤1,T是正弦函数.为求解方便,首先将区间 [R1,1]化到区间 [-1,1]上,为此令

其中a是新的自变量

摄动方程 (7)和 (8)化为

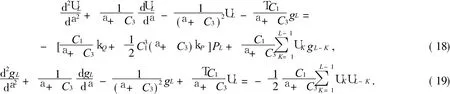
(18),(19)两式是变系数常微分方程,不能化为欧拉方程.下面讨论它的幂级数解法,将U L,gL和T展开成a的幂级数

式中:UL,K,gL,K和TK分别是 UL,gL和 T在a=0处的台劳展开式系数.将式 (20)代入方程 (18)和(19)中,可得到无穷个线性代数方程,递推求解这些方程组可知,每阶摄动的系数U L,K,g L,K由4个待定常数及 PL确定,假定 4个待定常数用 kL1,kL2,kL3,kL4表示.

2 待定常数的确定

为了确定每解摄动的 7个未知数eL,hL,PL及 4个待定常数 kL1,kL2,kL3,kL4,可以使用两个外边界条件,4个内力位移连续条件,一个摄动条件共 7个条件.将摄动展开式 (6)代入条件 (4)中,得到摄动形式的外边界的条件.

1)夹紧固定情形

2)滑动固定情形

在 r=b处,光滑中心和浅正弦波纹部分相接,将摄动展开式 (6)代入该处的内力、位移连续条件,得到摄动形式的方程

式 (22)中的上标 1表示采用光滑中心部分的值,上标 2表示采用浅正弦波纹部分的值.摄动条件取决于摄动参数的选取,这里选取无量纲中心挠度为摄动参数

由挠度与子午线的转角U*的关系式及外边界处挠度为零的条件,可得到

将光滑中心和浅正弦波纹膜片部分的转角的摄动展开式 (6)代入式 (24),得到摄动条件

7个未知数由方程 (21),(22)和 (25)确定,求得了未知数 eL,hL,PL,kL1,kL2,kL3,kL4的值后,由式 (6)可以得到中心挠度与荷载 P的关系式,根据内力、位移与转角、应力函数的关系,就得到了内力、位移的表达式.

3 数值算例与结果分析

计算结果表明:式 (20)中的U L,K,gL,K展开式系数随着K的增加迅速减小,所以只需取前 20项进行求和(K=0,1,2,3,… ,19).将U(2),g(2)摄动到三阶 ,运用 Matlab编辑程序求解方程组 (21),(22)和(25),求得相应于前三阶的 7个未知量 eL,hL,PL,kL1,kL2,kL3,kL4的数值(L=1,2,3),由此得到载荷作用下波纹圆板的特征关系式.

图1是由中心平台和浅正弦波纹环形板部分组成的波纹圆板的轴向截面,各有关数据为:E=104kg/mm2,g=0.3,h=0.22 mm,a=25 mm,L 0=6.6 mm,H=0.375 mm,光滑中心的半径 b=1.9 mm,边界夹紧固定.下面讨论在中心集中荷载作用下时其特征曲线.

图1所示波纹圆板的轴向截面可以由壳体子午线切线方向与 r方向的夹角T*用式 (26)描述出来.

图2 集中荷载下浅正弦波纹圆板的特征曲线Fig.2 Characteristic curve of circular plate with shallow sinusoidal corrugation under concentrated load

在中心集中荷载作用下,原先定义的荷载控制参数k P和k Q为k P=0,k Q=1,可以求出在中心集中载荷下边界夹紧固定浅正弦波纹圆板的特征关系为式中:Q0的单位是 kg;=-w 0的单位是 mm;为正表示挠度向下;为负表示挠度向上.根据式 (27)绘制的特征曲线如图2所示.图中是＞0时的特征曲线,Q0＜0时的特征曲线与之基本一致.由此可知,载荷反向对特征曲线的影响很小,这一结论可以从式 (27)中直接得出,因为挠度的二次项系数比一次项和三次项小很多.从图2可知,当/h)＜1.8(或＜5)时,特征曲线几乎是线性的,这一线性关系对于弹性元件的设计极其重要,采用这段特征曲线可以设计出精度高、线性度好的弹性元件.在这个范围之外,特征关系具有较为明显的非线性.

4 结 论

利用本文的求解方法可以得到近似解析表达式.文中算例表明:在中心集中载荷作用下,由于载荷-中心位移的关系式中的二次项相对很小,故载荷反向对特征曲线的影响不大;而且,由图中曲线可见,当载荷不大时,特征曲线是近似线性的,随着载荷的增大,特征曲线开始向上弯曲,明显地偏离了线性.

[1]Hersey M D.Diaphragms for aeronautic instruments[R].NACA TRNo.165,1925.

[2]Griffith A A.The theory of pressure capsules[R].Great Britain Aeronautical Research Council,R&M,No.1136,1928.

[3]Feodosev V I.Elastic Elements of Precision-Instruments Manufacture[M].Moscow:Oborongiz,1949:186-206.

[4]Hamada M.Numerical method for nonlinear axisymmetric bending of arbirary shell of revolution and large deflection analyses of corrugated diaphragm and bellows[J].Bulletion of JSME,1968,11(43):24-33.

[5]Andyewa L E.Elastic Elements of Instruments[M].Moscow:Masgiz,1981.

[6]王新志,王林祥,胡小方.波纹圆薄板的非线性振动 [J].应用数学和力学,1987,8(3):237-245.Wang Xinzhi,Wang Linxiang,Hu Xiaofang.Nonlinear vibration of circular corrugated plates[J].Appl.Math.Mech.,1987,8(3):237-245.(in Chinese)

[7]宋卫平,叶开沅.中心集中载荷作用下波纹圆板的变形应力和稳定性研究[J].中国科学 A辑,1989,32(1):40-47.Song Weiping,Ye Kaiyuan.Study of deformation stress and stability of corrugated circular plateunder the action of concentrated loads at the center[J].Sci.Sin.Ser.A,1989,32(1):40-47.(in Chinese)

[8]Liu Renhuai,Yuan Hong. Nonlinear bending of corrugated annular plate with large boundary corrugation[J].Applied Mechanics and Engineering,1997,2(3):353-367.

[9]袁鸿,刘人怀.均布载荷作用下带边缘大波纹膜片的非线性弯曲[J].力学学报,2003,35(1):14-20.Yuan Hong,Liu Renhuai.Nonlinear bending of corrugated diaphragm with large boundary corrugation under uniform load[J].Acta Mechanica Sinica,2003,35(1):14-20.(in Chinese)

[10]袁鸿,刘人怀.复合载荷作用下带边缘大波纹膜片的非线性弯曲[J].应用数学和力学,2003,24(4):367-372.Yuan Hong,Liu Renhuai.Nonlinear bending of corrugated diaphragm with large boundary corrugation under compound load[J].Appl.Math.Mech.,2003,24(4):367-372.(in Chinese)

[11]袁鸿,张湘伟.波纹壳的格林函数方法[J].应用数学和力学,2005,26(7):763-769.Yuan Hong,Zhang Xiangwei.Method of Green′s function of corrugated shells[J].Appl.Math.Mech.,2005,26(7):763-769.(in Chinese)

[12]袁鸿,张湘伟,刘人怀.波纹膜片的非线性稳定 [J].工程力学,2005,26(6):202-206.Yuan Hong,Zhang Xiangwei,Liu Renhuai.Nonlinear stability of corrugated diaphragm[J].Engineering Mech.,2005,26(6):202-206.(in Chinese)

[13]Liu Renhuai,Wang Fan.Nonlinear stability of corrugated shallow spherical shell[J].Int.J.of Applied Mechanics and Engineering,2005,10(2):295-309.

[14]袁鸿,刘人怀.均布载荷作用下波纹扁壳的非线性振动 [J].应用数学和力学,2007,28(5):514-520.Yuan Hong,Liu Renhuai.Nonlinear vibration of corrugated shallow shells under uniform load[J]. Applied Mathematics and Mechanics,2007,28(5):514-520.(in Chinese)

[15]袁鸿.波纹扁壳非线性振动的格林函数方法[J].中国科学 G辑,2008,38(5):592-599.Yuan Hong.Method of Green′s function of nonlinear vibration of corrugated shallow shell[J].Science in China,Series G,2008,38(5):592-599.(in Chinese)

[16]Wang Y G,Gao D,Wang X Z.On the nonlinear vibration of heated corrugated circular plates with shallow sinusoidal corrugations[J].International Journal of Mechanical Sciences,2008,50(6):1082-1089.

[17]刘人怀.波纹圆板的特征关系式[J].力学学报,1978,1(1):47-52.Liu Renhuai.Thecharacteristic relations of corrugated circular plates[J].Acta Mech.Sin.,1978,1(1):47-52(in Chinese).

[18]刘人怀.波纹环形板的非线性弯曲[J].中国科学 A辑,1984,27(3):247-253.Liu Renhuai.Non-linear bending of corrugated annular plates[J].Sci.Sin.Ser.A,1984,27(3):247-253.(in Chinese)

[19]Liu Renhuai. Large deflection of corrugated circular plate with a plane central region under the action of concentrated loads at the center[J].Int.J.Non-Linear Mechanics,1984,19(5):409-419.

[20]Liu Renhuai.Large deflection of corugated circular plate with plane boundary region[J].Solid Mechanics Archives,1984,9(4):383-406.

[21]Liu Renhuai,Li Dong.On the non-linear bending and vibrationg of corrugated circular plates[J].Int.J.Non-Linear Mechanics,1989,24(3):165-176.

[22]Liu Renhuai.Nonliear bending of a corrugated annular plate with a plane boundary region and a non-deformable rigid body at the center under compound load[J].Int.J.Non-liner Mechanics,1993,28(3):353-364.

[23]陈山林.浅正弦波纹圆板在均布载荷下的大挠度弹性特征[J].应用数学和力学,1982,1(2):261-272.Chen Shanlin.Elastic behavior of uniformly loaded circular corrugated plate with sine-shaped shallow waves in large deflection[J].Appl.Math.Mech.,1980,1(2):261-272.(in Chinese)

[24]袁鸿.波纹壳的摄动解法[J].应用力学学报,1999,16(1):144-148.Yuan Hong.The perturbation solution of corrugated shells[J].Chinese J.Appl.Mech.,1999,16(1):144-148.(in Chinese)

[25]Libai A,Simmonds JG.The Nonlinear Theory of Elastic Shells of One Spatial Dimension[M].Boston:Academic Press,1988:206-212.