挡墙对冲击波削弱作用的数值分析✳

李 鑫,吴桂英,贾昊凯

(太原理工大学理学院,山西 太原 030024)

随着世界范围内的恐怖袭击以及各种不可预知的爆炸所导致的恶性事件的增多,对爆炸冲击波的防护也越来越受到了学者们的关注,而挡墙作为一种十分有效的预保护建筑也被广泛地研究.爆炸问题属于高度非线性问题,理论研究难度较大,故目前模型实验和数值模拟是分析该类问题的两种常用方法.而模型实验重复性差,技术难度大,成本也非常昂贵,因此模拟分析成为目前解决此类问题的主要手段.Alex M.Remennikov[1]等通过有限元软件 AIR3D分析了复杂城市环境中爆炸冲击波的传播规律;Fernandoaz Alonso[2]运用超压-冲量-距离的特征曲线对 TNT炸药起爆后建筑物所受到的超压和冲量进行了分析.近年来,国内对此类问题也进行了大量的研究,王飞[3]等利用 ALE(Arbitrary Lagrange-Euler)算法和炸药爆轰产物的 JWL状态方程,对空气冲击波绕过障碍物的环流现象进行了数值模拟,得到了在爆源周围有障碍物的爆炸场初始发展和环流的情况;吴开腾[4-6]应用自行编制的 MM IC3D程序,模拟了在爆点附近有无障碍物的三维爆炸场的初始发展情况以及不同形状的防护挡墙对爆炸效应的影响.在实验方面,穆朝民[7]等采用试验的方法,对爆炸冲击波作用于防爆墙以及绕过墙体的规律进行了研究,采用压力传感器测压,获得了防爆墙前后不同距离的压力波形.以上研究大多局限于空中爆炸后冲击波遇到挡墙的传播过程及挡墙前后超压的分布,对于炸药起爆位置及挡墙的尺寸并没有给予足够的关注.

本文基于 ALE算法,采用 AUTODYN软件建立了包括空气、地面、炸药和挡墙在内的多物质分析模型,分析了炸药沙土地面上起爆情况下冲击波遇到挡墙时的传播过程以及不同挡墙尺寸对冲击波的削弱作用,其研究将为进一步的理论研究和实验研究提供有益的参考.

1 材料参数及计算模型

1.1 材料参数

空气状态方程采用理想气体状态方程

式中:密度d=0.001 225 g/cm3;绝热指数V=1.4;空气的初始能量密度设为 2.068×105m J/mm3.

炸药采用 TNT,密度 d=1.63 g/cm3,爆速 v=6.93×103m/s,爆压 p=2.1× 107k Pa.

状态方程为 JWL状态方程

式中:k=0.35,C1=3.74×105M Pa,C2=3.74×103MPa,r1=4.15,r2=0.9.挡墙采用型号为 C35的混凝土材料,采用 P-alpha状态方程及 RHT混凝土模型描述其本构关系.其初始密度d=2.75 g/cm3,体积模量 E=35.27 GPa,剪切模量 G=16.7 GPa,抗压强度e c=35 MPa,初始紧缩压力 p 0=23.3 MPa,完全紧缩压力 p=6 GPa.地面采用沙土材料,采用改良的 porous状态方程及 Drucker-Prager强度模型来描述沙土的本构关系,初始密度 d 0=1.67 g/cm3,剪切模量 G=76.9 MPa,卸载体积模量 E=0.5 GPa.其应力-压力、应力-密度及剪切模量-密度曲线均采用 D-P分段曲线.沙土及混凝土参数均来自 AUTODYN自带材料库,计算所需的具体参数见文献[8].

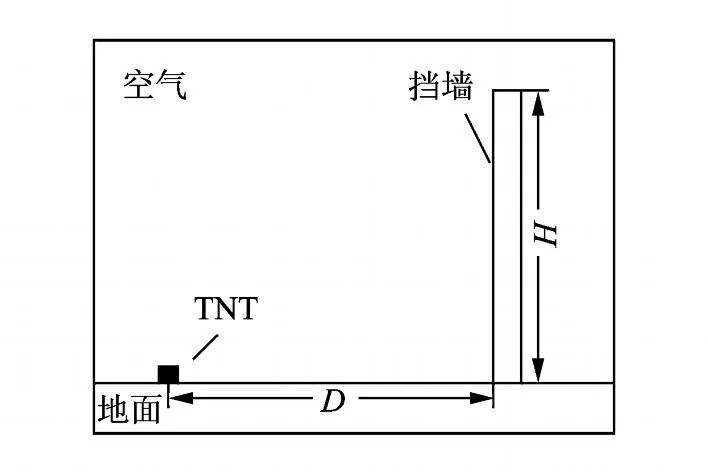
图1 计算模型Fig.1 Computational model

1.2 计算模型

图1中给出了计算的模型,空气将炸药和挡墙包围住,炸药位于挡墙中心正前方.其中:空气、沙土和炸药均采用欧拉单元,挡墙采用拉格郎日单元,空气和沙土采用可流出边界条件,挡墙底面固定于地面之上.整个模型采用单元尺寸为 5 cm的六面体单元.炸药质量 1.63 kg,划分成 8个 5 cm×5 cm×5 cm的六面体单元,采用中心起爆方式.计算中只考虑挡墙厚度为 250 mm的情况,分别计算了炸药比距离Z(=D/W1/3)=0.85 m/kg1/3和1.27 m/kg1/3,挡墙的高宽比 H/B=0.25,0.5,1.0,1.5,1.875,2.5等不同工况.为了节约资源,缩短计算时间,均采用 1/2模型进行计算.

2 计算结果分析

2.1 冲击波传播过程

在挡墙高度为 1 m,宽度为 1 m,炸药距离挡墙 1 m的情况下,研究了冲击波遇到挡墙的反射以及绕过挡墙继续传播的全过程.图2,图3中分别给出了不同时刻下冲击波传播的状态.图2为垂直于地面的中面切片压力云图,图3为地面上方平行于地面的切片压力云图.从图中可以清楚地看到冲击波遇到挡墙时的传播过程:冲击波遇到挡墙前壁后发生反射(t=0.5 ms),前壁上的超压陡然增大,但前壁边缘以外的冲击波并未遇到阻碍,因而波中的超压也没有增加,于是形成超压差,并引起空气的流动和波的产生;在前壁高压区的空气向前壁边缘外的低压区流动的同时,高压区的空气由边缘向内部逐渐得到稀释,形成稀疏波.在稀疏波的作用下,壁前面的气流向边缘运动(t=2 ms),但在运动过程中,由于受到顶部及两侧入射冲击波后面运动空气的影响而改变了运动方向,形成运动旋风,变成环流向前传播,并且在环流绕射到墙后继续运动时就会发生相互碰撞(t=4 ms),因此压力将会增大.绕射压力碰撞之后将会形成新的冲击波继续传播(t=6ms).

图2 中面内冲击波传播Fig.2 Propagation in the middle surface

图3 水平面内冲击波的传播Fig.3 Horizontal propagation

2.2 挡墙前后超压的分布

由图2,图3可知,爆炸冲击波在有挡墙时,将首先遇到挡墙反射,而后再绕射到挡墙后方,这样就延长了冲击波到达墙后的时间,并且挡墙还将吸收一部分冲击波能量,相对于没有挡墙的情况,冲击波将进一步衰减.由于绕射超压的汇聚,挡墙后的最大压力峰值并不是出现在紧靠挡墙背面的地方,而是距离挡墙背面还有一段距离.

表1 冲击波峰值到达时间Tab.1 Over-pressure reached time (ms)

表 1中给出了 Z=0.85 m/kg1/3和1.27 m/kg1/3在有挡墙和无挡墙的情况下,挡墙后相同位置冲击波峰值到达的时间.从表中可以看出,挡墙的存在明显地延长了冲击波峰值的到达时间,在这个过程中,冲击波将迅速地衰减.图4中给出了挡墙高度为1 m,宽度为 1 m,炸药比距离 Z=0.85 m/kg1/3和 1.27 m/kg1/3情况下,在有、无挡墙时挡墙后方水平方向上的压力峰值分布的情况.

从图4中可以看出,在无挡墙时,紧靠挡墙背面的地方,其压力峰值均远远大于有挡墙的情况,并且随着距离的增大迅速衰减;而有挡墙时,挡墙后最大压力峰值将距离挡墙背面一段距离,并且压力峰值随距离的变化较缓慢.随着距离的增大,两者压力峰值将趋于一致.

为了研究不同尺寸挡墙对冲击波削弱的影响,在炸药比距离 Z=1.27 m/kg1/3,挡墙高 H=1.5 m时,分别计算了挡墙高宽比 H/B=0.25,0.5,1.0,1.5,1.875,2.5及挡墙无限宽的情况.表2中给出了这些高宽比情况下挡墙后方的最大压力值及相应的比冲量.从图4(b)中可以看到,在无挡墙时,其最大压力 p=0.25 MPa,并且其比冲量 i=0.146 MPa· ms.对比表2中的数据可以看到,挡墙极大地减小了挡墙后方的压力峰值及比冲量,并且在挡墙高度一定的情况下,随着挡墙宽度的增加,其对冲击波的削弱作用越大,当 H/B≤0.25时,挡墙宽度的影响将很小.

图4 超压峰值随距离挡墙背面距离的分布Fig.4 Overpressuredistribution behind the wall

表2 不同挡墙尺寸下挡墙后超压及比冲量Tab.2 Over-pressure and impulse under different H/B

3 结 论

①应用 AUTODYN能很好地模拟爆炸冲击波遇到挡墙时的传播,并能对传播的过程进行详细的分析研究.②爆炸冲击波遇到挡墙时将产生反射和绕射,并且绕射超压将在挡墙后方汇聚,形成新的冲击波传播.③在挡墙作用下,挡墙背面冲击波峰值到达时间将被延长,相对于自由空气中,挡墙背面的压力峰值将大大减小;在挡墙高度一定的情况下,其宽度越宽,对冲击波的削弱作用越强,而当 H/B≤0.25时,挡墙宽度的影响将会很小.

[1]Remennikov A M,Rose T A.Modelling blast loads on buildings in complex city geometries[J].Computers&Structures,2005,83:2197-2205.

[2]Fernando Di az Alonso,Gonza′lez Enrique,Ferrada S.Consequence analysis by means of characteristic curves to determinethe damage to buildings from the detonation of explosive substances as a function of TNT equivalence[J].Journal of Loss Prevention,2008,21:74-81.

[3]王飞,朱立新,顾文彬,等.基于 ALE算法的空气冲击波绕流数值模拟研究[J].工程爆破,2002,8(2):13-16.Wang Fei,Zhu Lixin,Gu Wenshan et al.Numerical simulation of shock wave around-flow on basis of ALE algorithm[J].Engineering Blasting,2002,8(2):13-16.(in Chinese)

[4]吴开腾.挡墙对爆炸形成的空气冲击波防护效应的三维数值模拟研究[J].内江师范学院学报,2003,18(2):5-11.Wu Kaiteng.3D Numerical simulation of protective effect of the wall on explosive shock wave[J].Journal of Neijiang Teachers College,2003,18(2):5-11.(in Chinese)

[5]穆朝民,任辉启,李永池.爆炸冲击波作用于墙体及对墙体绕射的实验研究[J].实验力学,2008,23(2):169-174.Mu Zhaomin,Ren Huiqi,Li Yongchi.Experimental study of blast wave reflection and diffraction on a shelter wall[J].Journal of Experimental Mechanics,2008,23(2):169-174.(in Chinese)

[6]Zhou X Q,Hao H.Prediction of airblast loads on structures behind a protectivebarrier[J].International Journal of Impact Engineering,2008,53:63-375.

[7]都浩,李忠献,郝洪.建筑物外部爆炸超压荷载的数值模拟 [J].解放军理工大学学报,2007,8(5):413-418.Du Hao,Li Zhongxian,Hao Hong.Numerical simulation on blast over pressure loading outside buildings[J].Journal of PLA University of Science and Technology,2007,8(5):413-418.(in Chinese)

[8]Century Dynamics.AUTODYN 2-D&3-D.User′s Manual[M].2003.