共振隧穿微陀螺仪哥氏效应仿真及理论验证✳
李孟委,汪圣稀,杜 康,刘 俊,石云波
(中北大学 仪器科学与动态测试教育部重点实验室,山西 太原 030051)
0 引 言
1998年,在德国召开的陀螺技术研讨会上,美国陀螺专家 D.D.Lynch称哥氏振动陀螺 (Coriolis Vibratory Gyrosm,CVG)是一种重要的惯性技术,哥氏振动陀螺不仅具有所有的惯性品质,而且与另外两种固态陀螺(环型激光陀螺和光纤陀螺)相比,还具有可小型化的优势[1].
由于在硅材料上制作转子比较困难,因此绝大多数的微机械陀螺都是振动式陀螺,它们的工作基础都是利用 Coriolis效应实现驱动和检测模态之间的能量转移[2].中北大学张文栋、熊继军、薛晨阳等教授成功地将共振隧穿效应 (RTD)用于 MEM S加速度计中[3-6],使检测灵敏度有了很大提高,同时也激励了人们将 RTD用于 MEMS微陀螺的相关研究,这就是共振隧穿微陀螺仪.
本文首次提出了共振隧穿微陀螺仪的概念,目前的研究尚属于尝试阶段,要实现将共振隧穿效应和陀螺原理相结合这个想法,其结构的设计显得尤其重要.在结构设计中,如何进行正确的结构仿真计算是核心,特别像陀螺这种复杂器件,因为哥氏效应导致的三维运动的存在,更使得仿真计算十分困难[7],突显对结果的理论验证也非常必要.本文介绍了共振隧穿微陀螺的工作原理、陀螺结构模型和软件仿真方法,并从理论上推导了隧穿微陀螺正应力与哥氏力、角速度等参量的关系式,为结构设计仿真计算提供了理论验证方法,为微陀螺结构实体建模优化设计奠定了基础.
1 工作原理
1.1 哥氏效应
微机械陀螺是一种三维的惯性器件,3个方向分别设为 X,Y,Z,当把陀螺简化为一个质点时,其工作原理就可以直接用传统的哥氏理论表示.
哥氏加速度的形成原因:当动点的牵连运动为转动时,牵连转动会使相对速度的方向不断发生改变,而相对运动又使牵连速度的大小不断地发生改变.这两种原因造成了同一方向上附加的速度变化率,该附加速度变化率即为哥氏加速度.简而言之,哥氏加速度是由于相对运动与牵连转动的相互影响而形成的[8].
从质点模型来分析.如图1所示,设动坐标系 O′X′Y′Z′绕静坐标 OXYZ的 Z轴转动,在任一瞬时其角速度为k,角加速度为X的动点 M沿曲线 AB作相对运动,其中v r和 v e分别为相对运动速度和牵连运动速度.
哥氏加速度的表达式为 ak=2ω×vr.所以微机械陀螺的工作原理通常是在驱动方向 (X)输入驱动力,在另一个方向 (Y)输入角速度,最后通过各种方法获取检测方向 (Z)的哥氏力.
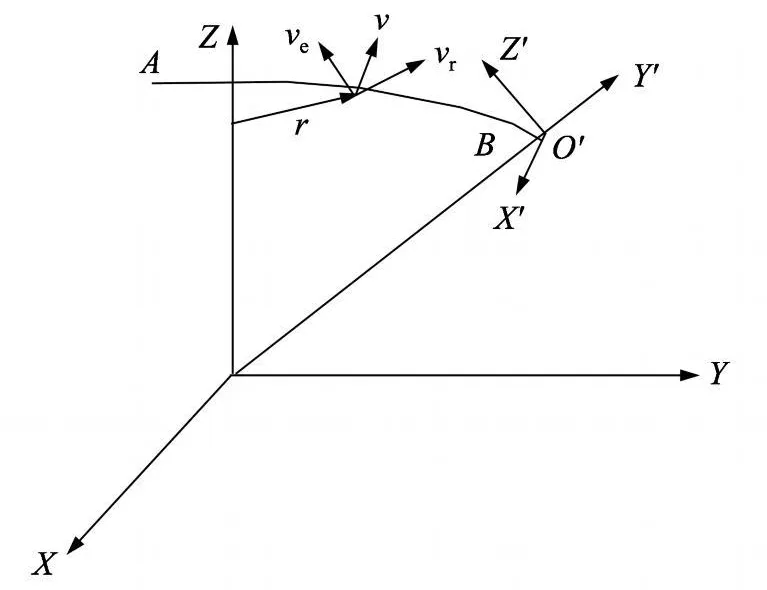
图1 质点运动Fig.1 Movement of particle
1.2 共振隧穿 RTD
GaAs基 RTD是一种超晶格纳米薄膜结构,核心是纳米级宽带隙材料中夹着纳米级窄带隙材料,通常贴在检测梁根部.从能带图上看,在导带上形成了双势垒的结构,两端是发射极与集电极.E0是势阱的第一量子化能级;E f是发射极的费米能级;E c为发射极导带底能级[9].
1)当没有偏压时,E0≥E f,双势垒薄膜没有发生共振,通过双势垒的电流为零.
2)对双势垒薄膜加偏压后,Ec<E0<Ef,双势垒薄膜发生共振,随着电压的增大,E0不断减小,透射几率增大,因而电流不断增大.
3)当偏压增大到 E0=E c时,电流达到最大值.
4)随着偏压进一步增大,E0<Ec,双势垒薄膜透射几率不断减小,故电流随着电压的增大而减小,呈负阻效应.
5)当 E0达到最小值时,通过双势垒的电流也达到最小值.
6)当电压再次增大时,E0不变,电流随着电压的增大而增大.

图2 共振隧穿示意图Fig.2 Schematic diagram of resonant tunneling
2 结构模型和 ANSYS仿真
2.1 结构模型
本文采用的微机械隧穿陀螺结构模型如图3,图4所示,参数尺寸如表1所示.

图3 隧穿陀螺整体结构模型Fig.3 The whole structural model of tunneling gyroscope

图4 隧穿陀螺局部结构模型Fig.4 Local structural model of tunneling gyroscop e

表1 陀螺结构参数Tab.1 Structural parameters of gyroscope
2.2 结构仿真
2.2.1 模态分析
该陀螺先在 X方向输入一个驱动力,使陀螺沿 X方向振动起来,驱动方式可以采用平板电容驱动或者电磁驱动,在仿真时将驱动力抽象为一个平面力,这个力可用 ANSYS的函数编辑器和加载器来实现;在 Y方向加载角速度或者角加速度(加载窗口如图5所示),加载时需要考虑加速度的原始坐标.
对模型进行正确的加载和条件约束后,便可计算求解并查看应力、速度和加速度等.这里选择检测由 Z方向哥氏力产生的 Y轴正应力,以及查看质量块的驱动速度.
通过 ANSYS模态分析[10],可以求得隧穿陀螺结构的固有特性.前四阶频率如图6所示,一阶模态振形如图7所示,二阶模态振形如图8所示.
从图6可知,一阶频率和二阶频率接近,相差 10% 左右,符合结构固有频率设计要求.从图7和图8的 ANSYS模态计算结果可以看出,一阶模态和二阶模态振型符合结构原理设计要求.

图5 哥氏效应加载窗口Fig.5 Loading window of Coriolis effect
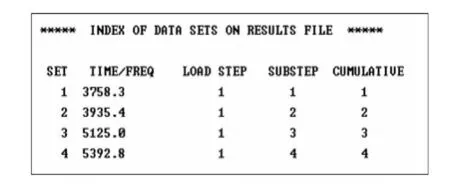
图6 ANSYS分析四阶频率的结果Fig.6 ANSYS results of four th order frequencies
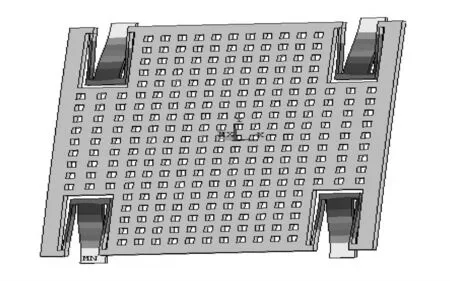
图7 一阶检测方向Fig.7 Detection direction of first order

图8 二阶驱动方向Fig.8 Driv en direction of second order
2.2.2 瞬态分析
为了分析陀螺结构的工作特性,需要对其进行 ANSYS瞬态分析[11].要求得隧穿陀螺驱动力幅值,可以假设这样一个力 F=f(time)=time,来找到最终驱动力的振幅.现取质量块上的一个点,并分析其在 X方向上的驱动位移,要求值小于结构要求的位移大小:60μm.
在瞬态分析后,查数据得:随着时间的变化,F也逐渐增大,当时间为 0.54 s,F为0.54μN时,驱动方向位移接近 60μm.对应的曲线如图9所示.
由于微陀螺哥氏效应的存在,在进行结构性能仿真计算时,必须考虑这种三维耦合效应的作用.下面就一些运动参量和结构参量作影响分析.
1)以角速度为自变量,其他条件不变,施加的载荷和计算结果如表2所示.提取各时间段的驱动速度数据如图10所示.
从表2数据和图10中,归纳出一个驱动速度和角速度的关系式

在这个仿真里,v0=0.501×10-4,k 0=100,k为角速度.各时间段的正应力如图11所示.
同样,从表2数据和图11中归纳出正应力与角速度的关系式

式中:k 0=100,W0=0.277×10-2,k为角速度.
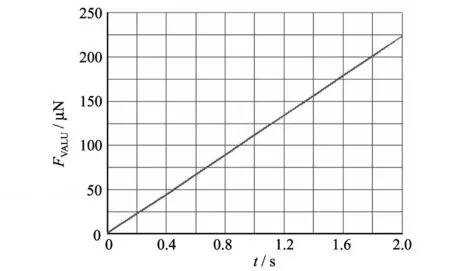
图9 瞬态分析驱动力幅值Fig.9 Driven force amplitude of transient analysis

图10 驱动速度随时间的变化关系Fig.10 Relationship between driving speed and time
2)以角加速度为自变量,其他条件不变,施加的载荷和结果如表3所示.

图11 检测正应力随时间的变化关系Fig.11 Relationship between detection normal stress and time

表3 角加速度影响分析表Tab.3 Analysis of angular acceleration impact
查看各时间段的驱动速度,如图12所示.
从表3数据和图12中,归纳出驱动速度和角加速度的关系式

式中:v0=0.178×10-3,a k0=100,a k为角加速度.
查看各时间段的正应力,如图13所示.

图12 驱动速度随时间的变化关系Fig.12 Relationship between driving speed and time

图13 检测正应力随时间的变化关系Fig.13 Relationship between detection normal stress and time
同样,从表3数据和图13中归纳出正应力与角加速度公式

式中:a k0=100,W0=0.988×10-3,a k为角加速度.
3 质量块受哥氏合力与检测梁根部正应力分析
1)将该陀螺的检测梁设为一个单端固支悬臂梁[12],长度为 L,厚度为 t,宽度为b,受支端载荷 F作用,结构示意图如图14所示.
根据工程力学,检测梁根部受到的最大正应力为[13]

挠度方程为

式中:M为弯矩;I为惯性矩;E为杨式模量;k为刚度系数.

图14 检测梁模型Fig.14 Model of detection beam

检测梁最大挠度为

式中:F c为质量块受到的哥氏力.
该结构检测梁根部最大正应力为

结构要求检测梁的最大挠度小于 60μm,故可求得哥氏力范围 F c≤5.3μN.
2)虽然角速度和角加速度对哥氏力都有影响,但从哥氏加速度的传统表达式 a k=2ω×v r中可以看出,角加速度是角速度的函数,所以哥氏效应的核心是哥氏力与角速度的关系式;而角速度会使质量块各点得到一个不同的线速度,因此各点的哥氏加速度是不一致的.
当只有驱动力,而没有角速度的时候,在质量块上各点的速度是一致的,设为 vx0;当存在角速度时,驱动速度会受角速度影响.从理论上讲,角速度会产生一个线速度,而且离中心越远,产生的线速度越大,vk=r k.
如图15所示,转动瞬间(即转动的角度很小θ)v k会对驱动方向提供分速度,故驱动方向的速度大小为


图15 角速度对驱动速度的影响Fig.15 Effect of angular velocity on drive velocity
结合哥氏力的理论式 F c=2m k×v得,整个质量块上的哥氏力合力为

可以化简为积分表达式

式中:mi为线密度,可以近似为
vx0通常很小,可以近似忽略,最终可以得到
式中:sinθ是常数值,结合检测梁根部最大应力的表达式

式中:sinθ是常数,代入表2中任意时间段的数据可以求得

故最终该模型检测梁根部正应力表达式为

4 结 论
分别将k=100,200,300,… 代入Wmax表达式进行计算,结果和仿真数据表2的结果几乎一致,证明理论计算结果和仿真结果相符,说明本文中提出的微陀螺结构仿真方法和理论验证方法可行,能够用于共振隧穿微陀螺的结构设计中.
[1]Lynch D D.Coriolis vibratory gyros[C].Stuttgart,Germany:Symposium Gyro Technology,1998.
[2]陈永.基于滑膜阻尼效应的音叉式微机械陀螺的研究 [D].上海:中科院上海微系统所,2004.
[3]Xue Chenyang,Tong Zhaomin,Zhang Binzhen,et al.A novel hydrophone based on the piezoresistive effect of resonant tunneling diode[J].IEEE Sensors Journal,2008,8(4):401-403.
[4]Xiong Jijun,Zhang Wendong,Mao Haiyang,et al.Research on double-barrier resonant tunneling effect based stress measurement methods[J].Sensors and Actuators A:Physical,2009,150:169-174.
[5]Hu Jie,Xue Chenyang,Zhang Wendong,et al.A piezoresistive microaccelerometer based on resonant tunneling heterostructures[J].Sensor Letters,2008,6:197-203.
[6]Li Bo,Zhang Wendong,Xie Bin,et al.Development of a novel Ga As micromechined accelerometer based on resonant tunneling diodes[J].Sensors and Actuators A:Physical,2008,143:230-236.
[7][美 ]罗伯特· D·库克,戴维· S·马尔库斯,迈克尔· E·普利沙著.有限元分析的概念与应用[M].关正西 ,强洪夫译.西安:西安交通大学出版社,2007.
[8]刘俊,石云波,李杰.微惯性技术[M].北京:电子工业出版社,2005.
[9]胡杰.介观压阻型加速度计的设计与性能测试 [D].太原:中北大学,2008.
[10]Shao Yunqiu.ANSYS8.0 Finite Element Analysis Example Navigation[M].Beijing:Chinese Railway Publishing House,2004:24-62.
[11]Xiaofeng Work Room Edit.Newest Classics ANSYS and Workbench Course[M].Beijing:Electronics Industry Publishing House,2004:408-420.
[12]王健.GaAs基共振隧穿压阻式声传感器研究[D].太原:中北大学,2007.
[13]西南交通大学.工程力学[M].北京:高等教育出版社,2004.

