基于四元数的彩色图像质量评价方法✳
王宇庆,刘维亚,王 勇
(1.中国科学院长春光学精密机械与物理研究所,吉林长春 130033;2.中国科学院研究生院,北京 100039)
经过各种图像处理过程所得到的图像的质量是衡量相应算法或者设备性能的重要指标之一,因此如何准确评价图像质量具有十分重要的意义.目前的图像质量评价方法可以分为两类:主观评价方法和客观评价方法[1].主观评价方法过程复杂、耗时长,结果易受观察者、测试条件和环境的影响,稳定性、可移植性差.客观评价方法依据模型给出的量化指标或参数衡量图像质量,是目前图像质量评价领域的研究重点.对于各种图像质量的客观评价方法,研究的目的是使评价结果与人的主观感觉相符.传统的图像质量客观评价方法(例如,均方误差 (Mean Square Error,MSE)和峰值信噪比 (Peak Signal Noise Ratio,PSNR)),都是基于对应像素点间的误差,即基于误差敏感的图像质量评价,由于并未考虑到人眼的视觉特性,因而经常出现评价结果与人的主观感觉不一致的情况.因此,许多研究者致力于寻找符合人眼视觉特性的图像质量评价模型,并提出了一些有效的算法(例如 Wang等人提出的结构相似度(SSIM)的图像质量评价方法[2-3],基于人类视觉系统 (Human Visual System,HVS)特性的图像质量评价方法[4-6]以及基于小波变换的方法[7]等),这些方法虽然在不同程度上克服了传统方法的不足,但是由于 HVS的复杂性,上述评价方法大多存在着在某些情况下评价结果与人的主观感觉不一致的问题.另外,这些方法需要待测图像与参考图像的尺寸完全一致,否则无法直接评价待测图像的质量.文献 [8]的方法虽然可以对与参考图像尺寸不相等的待测图像的质量进行评价,但是与以上所提及的很多图像质量评价方法一样,该方法仅能用于灰度图像而不是彩色图像.
人眼对亮度具有适应性,即在一幅复杂图像的任一点上只能识别几十种灰度级,但可以识别成千上万种颜色,因此彩色图像提供了比灰度图像更加丰富的信息.对于彩色图像的质量评价,目前所采用的方法大多是通过某种变换将彩色图像的亮度层次信息提取出来,采用灰度图像的质量评价方法评价所提取出来的亮度层次信息,从而得到对于该彩色图像的质量评价结果.这种方法显然忽略了图像中所包含的大量色彩信息,难以保证评价结果的准确性.
本文采用四元数表征彩色图像的结构信息,通过对彩色图像的四元数矩阵进行奇异值分解,并且计算待测图像与标准参考图像奇异值特征向量夹角的大小来度量两图像结构的相似程度,从而实现了对待测图像的质量评价.实验结果表明:对于尺寸相等的待测图像与参考图像,本文方法的评价结果要优于传统的 MSE,PSNR以及 SSIM方法,并且该方法也可以对与参考图像尺寸不相等的待测图像质量进行评价.
1 四元数和四元数矩阵
四元数也称超复数,由 Hamilton于1843年首次提出[9].一个四元数q由1个实部和 3个虚部构成

式中:a,b,c,d为实数;i,j,k分别代表超复数的 3个虚部的单位向量,并且满足如下关系

如果四元数 q的实部为 0,则称 q为纯四元数.由四元数组成的矩阵称为四元数矩阵.由于一般意义上实数或复数的矩阵求秩运算不能直接运用到四元数上,所以不能用复数域里的行列式计算方法.文献 [10]给出了一种复数伴随矩阵的定义,从而可以将四元数矩阵的运算转换为复数矩阵的运算,以利用一般意义上的复数矩阵求解.对于一个给定的四元数矩阵 A∈ HN×M(H表示四元数体),可以表示为A=A1+ A2 j,A1,A2∈ CN×M(C表示复数域),其复数伴随矩阵 χA∈ C2N×2M可以表示为[10]

式中:* 为共轭符号.文献 [10]详细介绍了四元数以及四元数矩阵,并且证明了四元数可以做奇异值分解.根据四元数奇异值分解的定义[11],对于任意一个秩为 r的四元数矩阵 A∈ HN×M,必有两个四元数酉矩阵U,V,使得

式中:符号 4表示共轭转置;∑r=diag(e1,e2,… ,er),ei(1≤i≤r)为实数,即为 A的奇异值;U,V分别称为四元数矩阵 A的左、右奇异值矩阵.U=∈ HN×N,V∈ HM×M.设 x=(e1,e2,… ,e r,0,… ,0)T,称为x四元数矩阵 A的奇异值特征向量.文献 [11]给出了一种根据由式 (3)得到的复数伴随矩阵对四元数矩阵 A进行奇异值分解的方法,本文根据该方法求得四元数矩阵的奇异值特征向量,从而将其作为评价对应于该四元数矩阵的彩色图像质量的一个重要依据.
2 彩色图像结构信息的四元数表示及质量评价方法

对于彩色图像的四元数表示,目前普遍采用文献 [12]提出的方法:令四元数的 3个虚部分量分别代表红 (R),绿(G),蓝(B)三基色,实部为 0,这样可以把彩色图像的每个像素都表示为一个纯四元数式中:r(x,y),g(x,y),b(x,y)分别表示图像中位于 (x,y)点处的红、绿、蓝的灰度值.这样,一副 N×M的彩色图像就可以看作是一个的纯四元数矩阵.四元数矩阵的奇异值特征向量表征了其能量特征,同样也可以将其用于表征相应彩色图像的能量特征.对于奇异值特征向量 x和 x^,其夹角表征了两向量线性相关的程度,夹角越小说明越接近线性相关,也是对 2个向量所张成的空间的线性相关度的度量[8].文献 [8]提出了一种基于奇异值特征向量夹角的图像质量评价方法,并且将其应用于灰度图像的质量评价,该方法可以对与参考图像尺寸不相等的灰度图像质量进行评价.本文采用度量两图像四元数矩阵奇异值特征向量夹角的方法度量二者所表征的彩色图像的结构相似程度,从而实现了对待测图像的质量评价.对于参考图像 I和待测图像^I ,评价指标 QISVD表示为

为保证计算精度,式中 k取两图像四元数矩阵秩的最小值,即别为两图像四元数矩阵奇异值特征向量的元素.QISVD取值范围为 [0,π/2],值越小说明待测图像与参考图像的结构越相似.图1给出了一组测试图像,图1(a)为原图像;图1(b)为原图像中添加密度为 0.02的高斯白噪声得到的噪声污染图像;图1(c)为模糊图像,是以 17×17模板对原图像均值滤波的结果.

图1 模糊和噪声污染的测试图像Fig.1 Test images with distortion of blur and noise
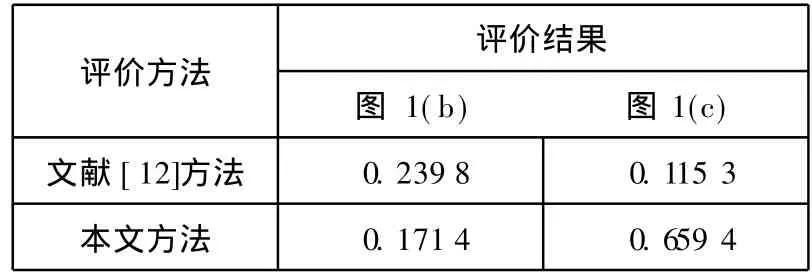
表1 图1中各降质图像的评价结果Tab.1 Assessment results for the distorted imagesin Fig.1
首先采用文献 [12]的方法得到彩色图像的四元数矩阵,然后根据文献 [11]给出的奇异值分解方法求得两四元数矩阵的奇异值特征向量,并且由公式(6)计算各降质图像与原图像的奇异值特征向量夹角,从而得到各图像的质量评价结果,如表1所示.由表1的评价结果可以看到,对于严重模糊的图1(c),该方法给出了较好的评价结果,而由人的主观感觉可知,图1(b)的质量要明显好于图1(c),这说明上述方法对于图像的细节损失不敏感,从而导致了对模糊图像的评价结果与人的主观感觉不一致,这也是 SSIM等图像质量评价算法所普遍存在的问题[13].人眼对图像的高频部分比较敏感,而图像的细节往往和高频部分有关,图像的局部方差较好地体现了图像的细节信息,所以可以通过分析图像局部方差的变化来分析图像的细节信息,或者也可以认为图像局部方差的分布包含了图像的大量结构信息[14].文献 [14]采用和 SSIM类似的形式通过对图像整体局部方差分布的统计实现了对图像质量的评价,该方法对模糊图像的质量评价取得了比较理想的效果.注意到文献[12]所提的彩色图像四元数表示方法中,仅将 3个虚部作为表示彩色图像的重要参数,因此本文将文献[14]中提到的局部方差作为表征图像结构信息的一个重要参数,与 RGB这 3个分量的亮度值共同组成对应于这一像素点的四元数表示,即

式中:Var(Ix,y)为图像 I的局部方差,即以像素点 (x,y)为中心的局部区域的方差.对于彩色图像,首先需要将其转换为 YUV空间,然后采用滑动窗口对 Y分量进行互不重叠的分块,得到每一分块的方差,即图像的局部方差.对于图像中包含 L个像素的图像分块 Ix,y,其内部像素为Z p,局部方差可以表示为

其中:

考虑到分块形状对图像结构的影响,对于包含在 Ix,y分块内的像素Zp,采用文献 [3]中提到的高斯加权的方法计算每一分块的均值和方差,表示为

由以上方法可以得到由局部方差以及彩色图像的 RGB分量组成的四元数以及对应于待测图像和参考图像的四元数矩阵,采用公式 (6)分别计算图1中的各降质图像与参考图像的四元数矩阵奇异值特征向量的夹角,从而得到了如表1所示的一组评价结果.
由表1可以看到,该方法对于图像的模糊失真的敏感程度有所提高,对于模糊程度比较严重的图1(c),该方法给出了较差的评价结果,这与人的主观感觉是相符的.
3 实验结果
为了进一步验证本文所提的方法,针对图2中各种类型的失真图像进行了评价并且将评价结果进行了对比.图2(a)为原图像;图2(b)为 JPEG2000压缩图像,采用文献 [17]的方法得到,压缩率为每像素 0.215 06比特;图2(c)为在原图像中添加密度为 0.15的高斯白噪声得到的噪声污染图像;图2(d)为采用 19×19的窗口对原图像均值滤波得到的模糊图像;图2(e)为仅对原图像 RGB这 3个分量中的G分量采用 29×29的模板均值滤波得到的模糊图像;图2(f)为原图像与常数 15相加得到的图像.实验中,计算局部方差的窗口采用文献 [3]的取值,大小为 11×11,高斯加权函数的方差为 1.5.首先将各图像转换到 YUV空间,针对 Y分量采用 MSSIM[3],WSSIM(加权的 SSIM方法)[3],MSE及 PSNR方法对各降质图像的亮度分量进行了评价,并且也采用公式 (6)计算了各降质图像与原图像亮度分量的奇异值特征向量夹角 (SVD),将各亮度分量的评价结果作为相应彩色图像的评价结果;然后采用相同的方法分别评价各降质图像与原图像 RGB分量的相似程度,并且将 3个分量评价结果的平均值作为相应待测图像的评价结果(Y分量的 RGB加权).表2给出了上述方法与本文方法 (QISVD)的评价结果.
严重的模糊导致了图像细节的大量缺失,因此根据人的主观感觉,图2(d)和图2(e)的质量要差于其余图像.由表2的评价结果可以看到,在各种评价方法中,仅本文所提的 QISVD方法对图2(d)和图2(e)给出了较差的评价结果.相对而言,图2(e)的质量略好于图2(d),QISVD对图2(e)的评价结果也要好于图2(d),这与人的主观感觉是相符的.在由亮度分量得到的评价结果中,MSSIM和 WSSIM方法因为对于模糊失真的敏感程度较低,因此对于模糊失真比较严重的图2(d)的评价结果好于图2(c),对于图2(e)的评价结果好于图2(b)和图2(c),这显然与人的主观感觉不符.M SE和 PSNR方法对于 JPEG2000压缩得到的图2(b)的评价结果要好于图2(f),对于图2(e)所给出的评价结果要好于图2(c)以及图2(d)和图2(f),这同样与人的主观感觉不一致.而 SVD方法对于图2(b)和图2(f)以及图2(c)和图2(e)都给出了相近的评价结果,这也不符合人的主观感觉.对于 RGB分量评价结果的平均值,MSSIM,WSSIM以及 MSE方法对图2中各降质图像的相对质量评价结果与对其亮度分量的评价结果基本一致.由于图2(e)是由仅对原图像绿色分量模糊得到的图像,因此 PSNR方法对 R和 B分量的评价结果趋于无穷,而总的评价结果亦趋于无穷.SVD方法对于图2(b)和图2(f)给出了相近的评价结果,另外对于图2(e)的评价结果要好于图2(c),这都与人的主观感觉不符.显然,对于图2中的各降质图像,本文所提的 QISVD方法则给出了较为合理的评价结果.

图2 多种失真类型的测试图像Fig.2 Test images with several types of distor tion
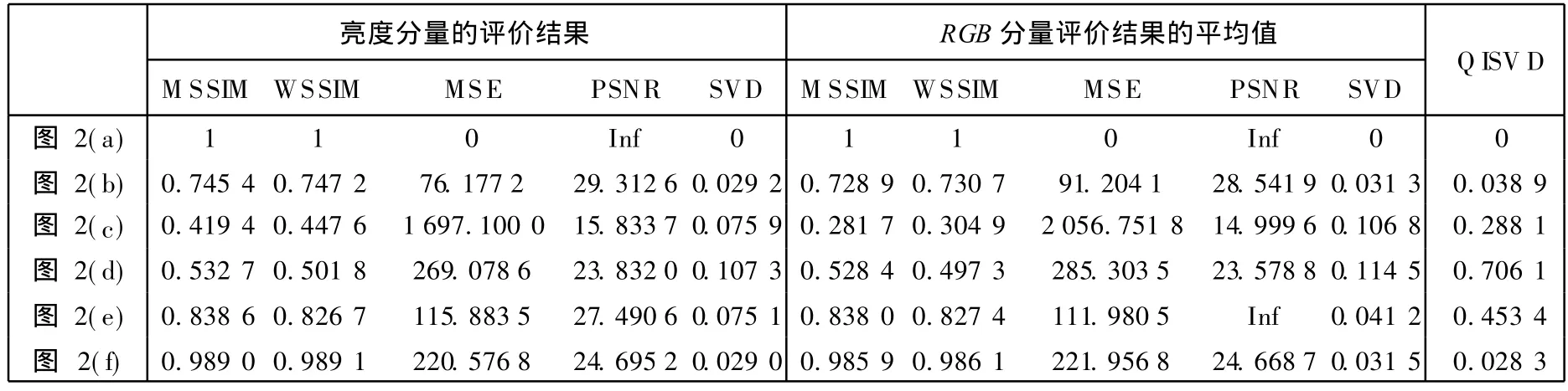
表2 采用多种评价方法对图2中各图像评价的结果Tab.2 Assessment results for the imagesin Fig.2 using several assessment methods
对图2(a)进行剪裁,采用本文的方法对剪裁后与原图像尺寸不相等的各图像的质量评价结果如表3所示(各图像的剪裁均以原图像左上角为基准).

表3 采用 QISVD方法对图2(a)剪裁后评价的结果Tab.3 Assessment results for the cutting images of Fig.2(a)based on QISVD
由表3的评价结果可以看到,尺寸越接近于原图像的剪裁图像,评价结果越好,这与人的视觉特性是相符的.对于图2中的各降质图像,也对其进行剪裁,同样以图像左上角为基准,将图2中与原图像尺寸相同的大小为 512×768的各降质图像剪裁为 480×720,同时也将其缩小为 384×576以及放大为600×900,以图2(a)为参考图像对其质量进行了评价,结果如表4所示.
显然,对于由同一种方法得到的彼此尺寸相等的剪裁以及缩放后的各降质图像,表4所给出的评价结果与表2所给出的评价结果是一致的,均与人的主观感觉相符.

表4 采用 QISV D方法对图2中各降质图像剪裁以及缩放后评价的结果Tab.4 Assessment results for the cutting and zooming distorted images in Fig.2 based on QISVD
4 结 论
本文采用四元数表征彩色图像的结构信息,将彩色图像亮度分量的局部方差作为影响图像质量的一个重要因素与 RGB这 3个分量共同组成彩色图像的四元数矩阵,通过计算两图像四元数矩阵奇异值特征向量夹角的大小度量二者的结构相似程度,从而实现了对待测图像的质量评价.实验结果表明:本文的方法比传统的 M SE,PSNR以及 SSIM方法更加符合人类视觉系统特性,并且也可以对与参考图像尺寸不相等的待测图像的质量进行评价.
[1]Eskicioglu A M,Sfisher P.A survey of imagequality measures for gray scaleimagecompression[C].Computing in Aerospace Conference.San Diego,USA:American Institute of Aeronautics and Astronautics,1993:49-61.
[2]Zhou Wang,Bovik A C.A universal imagequality index[J].IEEE Signal Processing Letters,2002,9(3):181-84.
[3]Zhou Wang,Bovik A C,Sheikh H R,et al.Imagequality assessment:From error visibility to structural similarity[J].IEEE Transactions on Image Processing,2004,13(4):600-612.
[4]Mauro Barni,Franco Bartolin,Alessia De Rosa.HVSmodelling for quality evaluation of art images[C].IEEE 14th International Conferenceon Digital Signal Processing.Santorini,Greece,2002:91-94.
[5]Westen S J P,Lagendijk R L.Perceptual image quality based on a multiple channel HV S model[C].IEEE 1995 International Conference on Acoustics,Speech,and Signal Processing.Detroit,MI,USA:IEEE,1995:2351-2354.
[6]Maloigne F.Spatio-temporal characteristics of the human color perception for digital quality assessment[C].IEEE Signals,Circuits and Systems ISSCS 2005 International Symposium.New York:IEEE,2005:203-206.
[7]Beghdadi A,Pesquest-Popescu B.A new image distortion measure based on wavelet decomposition[C].IEEE 1995 International Conferenceon Acoustics,Speech,and Signal Processing.Paris,France:IEEE,2003(1):485-488.
[8]骞森,朱剑英.基于奇异值分解的图像质量评价[J].东南大学学报(自然科学版),2006,36(4):643-646.Qian Sen,Zhu Jianying. Image quality measure using singular value decomposition[J]. Journal of Southeast University(Natural Science Edition),2006,36(4):643-646.(in Chinese)
[9]冉瑞生,黄廷祝.基于四元数矩阵奇异值分解的彩色图像识别[J].计算机科学,2006,33(7):227-229.Ran Ruisheng,Huang Tingzhu.The recognition of color images based on the singular value decompositions of quaternion matrices[J].Computer Science,2006,33(7):227-229.(in Chinese)
[10]Zhang F.Quaternion and matrices of quaternion[J].Lin.Alge.Appl.,1997,215:21-57.
[11]Bihan N L,Mars J.Singular value decomposition of quatemion matrices:a new tool for vector-sensor signal processing[J].Signal Processing,2004,84(7):l177-1199.
[12]Pei S C,Cheng C M.A novel block truncation coding of color images by using quaternion moment preserving principle[J].IEEE Transactions on Communications,1997,45(5):583-595.
[13]Cadik M,Slavik P.Evaluation of two principal approaches to objective image quality assessment[C].Proc ofthe 8th lnternational Conferenceon Information Visualisation.London:IEEE Computer Society,2004:513-518.
[14]Santiago A F.Image quality assessment based on local variance[C].Proceedings of 28th IEEE EM BS Annual International Conference.New York,USA,2006:4815-4818.
[15]Taubman D S,Marcellin M W.JPEG2000: Image Compression Fundamentals,Standards and Practice[M].Kluwer Academic Publishers,2001.

