三次样条插值在变径内腔重建中的应用✳
王会峰,刘上乾,汪大宝,卢 泉
(西安电子科技大学 技术物理学院 ,陕西 西安 710071)
0 引 言
药室内腔容积是炮身的一个重要参数,它会影响装填密度,进而影响膛压和初速的修正值.而这些参数的变化会直接影响着射程和弹丸的内外弹道轨迹及其弹着点的精度和发射的安全性,因此有必要对其进行高精度测量.从目前国内的测量方法来看,主要有音频检测、灌水法测量等;而这些方法都存在效率低下、操作复杂等缺点,无法满足现代靶场和用户对火炮容积参数的高效、自动化、高精度检测的需求.
本文陈述的直径-进深内腔容积检测方法具有高效、高精度自动化等特点;然而,由于测量本身的特征,使得测量部在间歇进深移动过程中的各个测量点之间的直径值难以准确地估计,同时由于采用传统的分段低次线性插值法由于插值基函数的不连续性影响了容积重建的精度和重建后的视觉效果,为此提出了基于三次样条插值函数的变径内腔截面圆直径的插值方法,该方法不仅使得插值后的重建效果得到了改善而且提高了容积的测量精度.
1 变径内腔结构和直径-进深测量原理
药室内腔截面的结构形状如图1所示,包括圆锥体部分和过渡圆锥体部分等.随着炮弹发射数目的增多,过渡圆锥体部分会发生变化,其位置会往身管方向移动,使内腔的体积增大.由几何理论可知,内腔空间容积和长度要素以及该段横截面的直径有关,因此有必要从分析这两个测量要素入手探索变径内腔空间容积的高效测量手段.

图1 药室结构示意图Fig.1 Structure of powd er chamber

图2 直径-进深药室测量原理Fig.2 Diameter-length volume measurement principle
基于直径-进深的内腔容积测量装置主要由炮尾辅助装置,进深高精度控制和测量机构,直径测量光电成像测量部,图像和数据处理单元等部分组成.如图2所示,炮尾辅助装置用来实现测量装置和身管的连接;进深高精度控制测量机构实现高精度进深控制;直径测量光电成像部完成光电图像的获取.测量部在进深系统的推动下进入标定机构,径向相隔 90°安装测量触头;测量触头先在标定环中进行标定,然后进入腔体内部在定中装置的支撑下开始测量,高精度进深机构上装有光栅尺用来记录进深距离,测量部每隔一定的步长停下通过计算机读取标尺靶的数据,从而实现对直径的测量.
设测得内腔截面的两个直径 d x,d y相对于标定环的变化量为Δx,Δy,因此,各截面两个垂直方向的平均直径为 di

式中:d cp为定标环直径;Δdi为第 i个截面尺寸 d x,d y对定标环的变化量的平均值.

通过光栅编码器可直接获得测量部沿轴的高精度进深位移,在测量部进行第 i次间歇移动时的位移为hi,则第 i次移动测得的圆台体积为

假设测量在 N步内完成,则药室的容积可以由式 (4)得到

为了提高测量精度要需要提高测量步数,但是步数越多测量效率就越低,因此在相邻点之间需要对直径-进深函数做必要的插值,以提高测量精度[1-2].
2 三次样条插值模型[3-4]
根据变径内腔的结构特点和实际测量数据的情况,对变径内腔的结构形状利用插值算法建立数学模型.当节点增多时,应用分段低次插值,有较好的局部性,插值函数具有一致的收敛性,能保证插值函数的连续性,但是光滑性差.根据药室的结构特点,通过理论和实验分析,利用药室的长度数据和横截面的直径数据,采用三次样条函数插值算法,能保证各段之间连接处的足够光滑性,既具有分段低次插值的一致收敛性和计算的稳定性,又具有高次插值的整体的足够光滑性,可以满足测量要求,达到较好的效果.
2.1 三次样条函数定义
设 [a,b]上有插值节点 a≤x0<x1<… xn≤b,对应值为 y0,y1,… ,yn,若函数 S(x)满足:

2)S(x)在每一小区间 [xj,xj+1]上是三次多项式,其中 j=0,1,2,… ,n-1;
3)S(x)在 [a,b]上有连续的一阶、二阶导数,则称 S(x)为三次样条插值函数.
2.2 插值函数的表达式
三次样条函数 S(x)是一个分段三次多项式,在每一个子区间 [x j-1,x j]上分别是一个三次多项式,因此 S″(x)在每个子区间 [xj-1,xj]上是一个一次多项式.如果 S″(x)在小区间 [xj-1,xj]的两个端点值已知,为

设各子区间的长度 hj=xj-xj-1,j=1,2,…,n.根据拉格朗日插值多项式,则函数 S″(x)在子区间[x j-1,x j]上的一次拉格朗日插值多项式为

将式 (7)积分两次得

式中:c1,c2可由插值条件 S(xj)=yj确定.因此插值函数 S(x)的表达式

式 (9)是利用二阶导数 Mj(j=0,1,… ,n)来表示插值函数 S(x),称为 S(x)的 M表达式.
2.3 M关系式
式 (9)是 S(x)的函数表达式,其中含有参数 Mj(j=0,1,…,n),而实际上是未知的,只有求出 Mj之后,S(x)才能确定.由式 (9)的推导过程可知,S(x)满足插值条件式 (5),因而 S(x)在整个区间[a,b]连续;由式 (6)可知,S″(x)在节点连续,显然 S(x)在每个子区间上是三次多项式.因此利用 S′(x)在节点的连续性来确定参数 Mj.对式 (9)两边求一阶导数,得

由此可得 S(x)在 xj的左导数为


将式 (12)中的 j换成 j+1,即得 S(x)在 x j的右导数
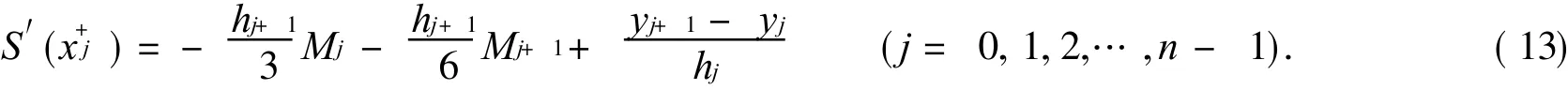
由于 S′(x)在区间 [a,b]连续,故在 x j的左右导数相等,即式 (12)和式 (13)得


式中:

式 (15)表达 S(x)在插值节点的二阶导数 Mj(j=0,1,…,n)之间的关系,因而称为 M关系式.
2.4 边界条件与基本方程组
式 (15)中有 n-1个方程,但有未知数 Mj(j=0,1,…,n)n+ 1个.要得到唯一解需增加两个方程,或减少两个未知数.根据火炮药室的结构特点,在药室的两端,即区间 [a,b]的端点 a和 b(即 x0和 xn)处对插值函数附加限制条件,称为边界条件.通过分析药室的边界条件,应满足

因此关于 Mj的基本方程组为

在 xj-1的右导数为
此方程组是三对角形方程组,可采用追赶法求解(略).
2.5 插值函数计算
由上述分析可知,插值函数 S(x)的具体表达式不仅决定于对区间 [a,b]的剖分和被插函数在各分点的函数值,而且决定于 S(x)在各分点的二阶导数值 Mj(j=0,1,…,n);而求 Mj(j=0,1,…,n),需先解基本方程组;要使基本方程组有唯一解,又需要预先给定边界条件并根据边界条件调整基本方程组.因此,该函数插值的基本计算步骤可归纳为:
第一步.输入初始数据 xj,yj(j=0,1,…,n);
第二步.对于 j=1,2,… ,n,按式 (6)计算 hj;
第三步.对于 j=1,2,… ,n-1,按式 (16)计算 _j,λj,d j;
第四步.根据边界条件,用追赶法解基本方程组式 (18),求出 Mj(j=0,1,…,n);
第五步.对于 j=1,2,… ,n,按式 (9)计算 S(x)各项的系数,并求得 S(x)在各子区间 [xj-1,x j]上的表达式;
第六步.根据需要输入若干个插值点x~i(i=1,2,…,N),分别按x~i(i=1,2,…,N)所在子区间S(x)的表达式计算S(x~i)(i=1,2,…,N),并输出结果.
本函数插值具有明显的优点,当 max hj→0时,S(x)一致收敛于 f(x),且 S(x)的一阶和二阶导数也分别收敛于 f(x)的一阶和二阶导数,因而只需对区间 [a,b]细分就可以提高精度,不必提高样条函数的次数.又基本方程组的系数矩阵总是严格对角占优的,因此基本方程组的解存在且唯一,S(x)存在且唯一.并且解基本方程组和计算插值S(x~)的稳定性都很好.
3 药室容积高精度修正重建和计算算法
设以上插值函数的区间 [a,b]中的 a和 b分别对应于药室的两端,x0,x1,…,xn对应于由测长机构测出药室的进深位置数据,2y0,2y1,…,2yn分别对应于在位置 x 0,x 1,…,xn时该横截面药室的直径数据.利用以上研究的插值函数,可得火炮药室体积的计算公式

式中:x0=a,xn=b.
可根据测量数据按被测管状容器的实际形状建立起空间三维模型,并可同时以不同的颜色在同一幅图像中按管状容器的设计参数建立理想的空间三维模型,以便直观而准确地了解其实际状况以及其变化情况.
在三维空间直角坐标系 Oxyz中,根据 3节中得到的插值函数 S(x),可得 xy平面上的插值曲线y=S(x),即可写成如下方程的形式

则以 x轴为旋转轴,以插值曲线 y=S(x)为母线得到的旋转面方程为

因此,此曲面就是其实际空间的三维结构模型.
4 试验结果
实验选用某变径内腔为测试对象,图3是根据表1的采样数据,利用以上研究的算法绘出的插值函数曲线图,和根据插值函数建立的空间三维表面效果图.图4是利用分段低次线性插值算法插值曲线和表面重建效果.可知经过样条插值后的三维重建效果优于分段低次线性插值的结果.
通过式 (19)分别对图3和图4插值后的曲线进行容积值的计算,并且和灌水法测试结果进行对比,
如表2所示.

图3 样条插值三维表面重建Fig.3 Three dimension surface reconstruction with cubic spline

图4 分段低次插值三维表面重建Fig.4 Three dimension surface reconstruction with subsection low order interpolation

表1 试验采样数据Tab.1 Sampling data (mm)
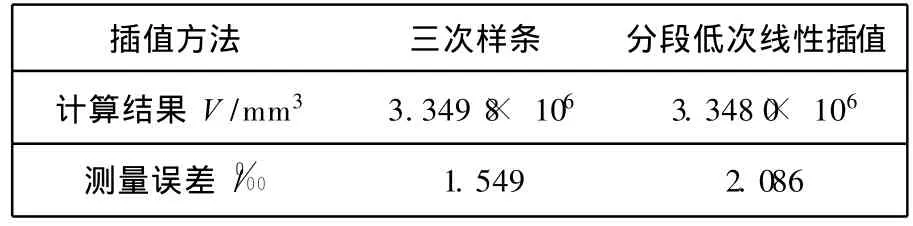
表2 不同插值方法容积计算结果Tab.2 Volume results calculated by differentinterpolation algorithms
5 结 论
将三次样条插值算法引入基于直径-进深光电成像式变径内腔容积测量和三维重建中,有效地克服了直接累加和分段低次线性插值法,由于插值基函数的不连续性对变径内腔容积重建的精度和重建后的视觉效果.该方法不仅使得插值后的重建效果得到了改善,而且在一定程度上提高了容积的测量精度[5-6].实践证明:该算法稳定运算量小,可用于工程上实时计算.
[1]吴文明,高立民,吴易明,等.利用三次样条插值提高自准直仪的准确度[J].光子学报,2007,36(8):1561-1564.Wu Wenming,Gao Limin,Wu Yiming,et al.Improving precision of autocollimation with cubic spline interpolation functions[J].Acta Photonica Sinica,2007,36(8):1561-1564.(in Chinese)
[2]王永仲.智能光电系统[M].北京:科学出版社,1999:34-40.
[3]李庆扬,王能超,易大义.数值分析[M].武汉:华中理工大学出版社,1986:16-26.
[4]邓建中,刘行之.计算方法[M].西安:西安交通大学出版社,2001:48-88.
[5]Heras H D L.Comparison of interpolation functions to improve a rebinning-free CT-reconstruction algorithm[J].Zeitschrift Für Medizinische Physik,2008,18:7-16.
[6]Kong V P,Ong B H.Constrained space curve interpolation with onstraint planes[J].Computer Aided Geometric Design,2007,22(6):531-550.

