能量系统广义换热网络优化的蒙特卡罗SCDD法

姜 慧,崔国民,倪 锦

(上海理工大学热工程研究所,上海 200093)

0 引 言

能源紧缺是当今全球面临的迫切而又严峻的问题,在积极寻求新能源的同时,如何提高现有能源的利用效率成为重要研究课题。以往,提高能源利用的研究方向主要集中在改进单体用能设备的结构,使之具有更高的效率,而忽略了从能量系统的集成方面入手,考虑如何设计整体用能系统,使得现有的能量系统获得最佳的能量利用组合形式。

能量系统的广义换热网络[1,2]是指:将各种用能设备等效为广义换热器,进而以广义换热器为基础按照能流走向而构成广义换热网络。用能设备广义换热网络的优化是指:应用一定的数学优化方法,针对不同结构和参数的广义换热网络,获得最佳的结构组合形式以及参数设置方式,使广义换热网络代表的用能量系统在满足各种约束条件下,总能效率最高。

由于数学模型本身的非线性及分布参数特性,使得能量系统广义换热网络的优化变成混合整数非线性规划问题 (MINLP),一般的优化方法难以获得全局最优解。针解这个难题,本文提出广义换热网络的蒙特卡罗SCDD混合算法,SCDD[4]法具有计算效率高的特点,而蒙特卡罗方法[3]的引入可使SCDD算法不会陷入局部最优解的僵局,提高了算法的全局搜索能力。

1 能量系统的广义换热网络

1.1 广义换热器

用能设备可分为能量交换设备和能量转换设备。能量交换是指能量在不同物体间的传递和交换,而忽略次要的能量转换成分;能量转换设备包含了不同能量形式的转换过程,一般情况下忽略能量交换的成分。对用能设备进行分类有利于依据用能设备自身的特点,分别对用能设备进行等效转化,具体方法为:

热量交换设备近似为换热设备,依据热量传递方向即可分出冷热流体,而其设备效率则可以用来获得换热参数,因此该类设备等效化过程中只需要广义换热器基本参数的确定;而能量转换设备,一般很难直接获得冷热流体,因此需要在等效化过程中依据能量守恒定律,构造一种甚至两种虚拟流体,以此来完成广义换热器形式及性能上的等效转化。

广义换热器转化的优点:在系统集成的过程中,避开了建立复杂的针对用能设备过程机理的数学模型,将能量系统参数间的耦合关系转化为换热器换热面积、换热系数与进出口参数之间的函数关系,大大简化了其中的计算过程。

1.1 广义换热网络及其模型

在将单个用能设备等效为广义换热器的基础上,将用能系统等效为广义换热网络。旨在表示用能设备的前后连接关系,不同的结构和参数代表不同的能量系统。

为获得能量系统的最佳组合形式,参考换热网络的超结构模型,根据广义换热器的特点,建立用能系统的广义换热网络超结构模型。如图1所示:

图1是针对余热利用系统构建的一个3级2设备的用能系统的广义换热网络模型,图中的换热器即等效后的用能设备。广义换热器的性能参数代表用能设备的结构性能参数:换热面积代表用能设备的容量,进出口流量及温度对应用能设备一定的性能参数 (如进出设备的能量品质、流量、压力等)。换热系数对应用能设备的本身的效率。

图1 广义换热网络的分级超结构模型Fig.1 Generalized heat exchanger Network super structure

2 广义换热网络的蒙特卡罗SCDD方法

蒙特卡罗属于随机性方法,具有全局搜索能力而不会陷于局部最优解的特点。总体思想为将蒙特卡罗方法与SCDD方法结合,利用蒙特卡罗法的全局搜索能力克服函数的多峰性。具体方法:应用蒙特卡罗方法获得广义换热网络能流的初始分配比例,然后利用SCDD法对初始能流分配比例下的目标函数进行求解,以此获得得最佳广义换热网络的结构,该方法克服了单独使用SCDD法遇到的局部最优解的缺陷,使得在保证运算效率的同时,保证了解的质量。

2.1 目标函数

本文以相同一次能源用量下的总能利用效率为目标函数。在一次能源用量相同的情况下,结合优化方法求最小值的特点,将总能利用效率转化成如 (1)形式:

式中:λ为分配比例;η为总能利用效率,具体表示方法如式 (2):

式中:λNin第N级第in个用能设备获得余热百分比;ηlNin第N级第in个用能设备做功或换热的能量百分比;ηmNin第N级第in个用能设备产生的余热百分比。

约束条件:

将上述约束条件抽象为

2.2 蒙特卡罗法生成能流初始分配比例

采用蒙特卡罗方法时,需要产生各种概率分布的随机变量。本文采用在[0,1]上均匀分布的随机变量。伪随机数的迭代公式为

式中:h为乘因子;M为模数。第1式称做以M为模数 (modulus)的同余式,即以 M除hxn后得到的余数记为xn+1。当给定了一个初值 x0,计算出的r1,r2,…即为在[0,1]上均匀分布的随机数。

若广义换热网络的级数为 N1,设备数为N2,则能流初始分配比例的规则如下:

第1级初始分配比例表示为

式中:j=1,…,N2。

第i级的初始分配比例为

第N1级的初始分配比例为

利用如上方程,可获得能量系统的能流初始分配比例。

2.3 SCDD法优化能流初始分配比例

SCDD法是求解带等式约束和不等式约束非线性规划问题的优化方法,具有算法结构简单,速度快的优点。SCDD法优化能流初始分配比例的步骤如下:

(1)构建可行域G为

以及由约束条件组成的综合约束函数S:

(3)若满足上述关系,则停止迭代,计算结束。否则,比较 Sz(λk+1)和 Sz(λ):

a.若 Sz(λk+1)≥Sz(λk),则缩短步长,令 tk+1=γ◦tk(γ＜1)。

b.Sz(λk+1)＜Sz(λk),再检查是否有则缩短步长,‖λk+1λk‖≥tk?,若有,取tk+1=σ◦tk(σ ＜ 1);否 则,取 tk+1=

因此初始可行域近似为

(2)从初始比例 λ(0)出发,对目标函数 Sz按负梯度方向以步长t0进行下降迭代。若所得的比例满足约束,则从此比例出发,再对 Sz下降迭代,否则,从此点出发对综合函数 S(λ)按负梯度方向以步长τ=β◦t0进行下降迭代。一般地,当已得比例属于第k次可行域Gk={λ|λ∈En,S(λ)≤Sk},则从比例rk出发对Sz(r)按λk的负梯度方向以步长tk迭代,并要求 λk+1属于Gk。若rk+1不属于Gk,则从此比例出发取步长τk+1=β◦tk对Sz(r)进行下降迭代直到属于Gk的比例。然后检查是否满足收敛准则:最后,令 Sk+1=α◦tk+1进行下一次迭代。

利用蒙特卡罗随机抽样技术获得不同的初始比例,利用SCDD法对由蒙特卡罗法获得的初始比例进行优化,寻求最佳的组合形式与能流分配比例,使得总能利用效率最佳;由于蒙特卡罗法搜索能力强,结合SCDD的求解效率高的优点,两者综合最终获得能量系统的全局最佳分配比例。

3 算 例

以图2所示的能量系统的广义换热网络超结构为例,其中燃气轮机运行参数如表1所示,分别利用SCDD法和蒙特卡罗SCDD法优化,比较算法的效率和质量。旨在寻求最佳的余热设备组合形式与能流分配比例,优化结果见表2,3。

图2 广义换热网络的结构Fig.2 Structure of generalized heat exchanger Network

表1 燃机运行参数Tab.1 Running parameters of gas turbine

表2 SCDD法优化后的结果Tab.2 Result of optimization with SCDD

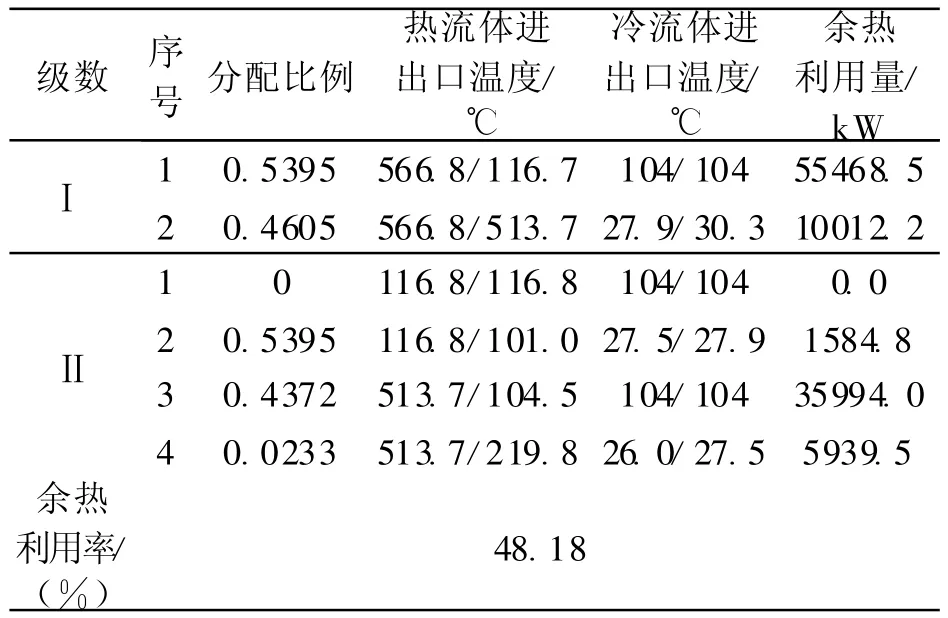
表3 蒙特卡罗SCDD法优化后的结果Tab.3 Result of optimization with SCDD and Monte Carlo

从表2,3中可以看出,由于能量系统广义换热网络的优化属于复杂的混合整数非线性规划问题,其性能曲线呈现严重的非凸非凹形式,常规的优化方法容易陷入局部最优解。本文所采用蒙特卡罗法SCDD法可以有效地跳出局部最优解,进而获得能量系统广义换热网络的全局最优解,为能量系统广义换热网络的优化提供了一种新的思路。

4 结 论

本文在能量系统的广义换热网络分级超结构模型的基础上,将蒙特卡罗法与SCDD法相结合,对广义换热网络进行了优化,得到如下结果:

(1)蒙特卡罗方法具有极强的搜索能力,能够有效获得广义换热网络中的能流初始分配比例,扩大了优化求解的搜索域。

(2)将SCDD法应用在广义换热网络能流比例的优化,获得了最佳能流分配比例,提高了能量系统的总能利用效率。

总之,本文对蒙特卡罗SCDD混合算法在能量系统的广义换热网络优化进行了探索,且得到了较好的结果,为能量系统的广义换热网络的优化提供了一新的解决途径。

[1]Yee T F,Grossmann I E.Simultaneous optimization models for heat integration:Heat exchanger network synthesis.Computer Chem.Eng,1990,14:1165-1184

[2]姜慧,崔国民,李瑜.能量系统优化中的超结构建模[J].石油化工,2008,5(37):594-596

[3]朱本仁.蒙特卡罗方法引论[M].济南:山东大学出版社.1987.

[4]胡毓达,翁史烈,秦士元.＜SCDD＞法的两个应用及计算程序[J].上海交通大学学报,1979,(4):67-70.